北京英才苑学科专家组 安振平 审定
2003-2004学年度下学期
高中学生学科素质训练
高一数学同步测试(11)
平面向量的数量积、平移
一、选择题(每小题5分,共60分,请将所选答案填在括号内)
1. 给出以下4个命题:
① 若![]() 则对任意向量
则对任意向量![]() ,有
,有![]() ;
;
② 若![]()
![]() ,则
,则![]() ;
;
③ 若![]()
![]() ,则
,则![]() ;
;
④ 若![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 时成立.
时成立.
其中真命题的个数为 ( )
A.1 B.2 C.3 D.4
2.若![]() ,
,![]() ,则
,则![]() 的数量积为 ( )
的数量积为 ( )
A.10![]() B.-10
B.-10![]() C.10
C.10![]() D.10
D.10
3.若将向量![]() 围绕原点按逆时针方向旋转
围绕原点按逆时针方向旋转![]() 得到向量
得到向量![]() ,则向量
,则向量![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.在矩形ABCD中,![]() ,当
,当![]() 时,
时,
![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.2 D.3
C.2 D.3
5.已知A(5,7),B(2,3),将![]() =(4,1)平移后的坐标为 ( )
=(4,1)平移后的坐标为 ( )
A.(-3,-4) B.(-4,-3) C.(1,-3) D.(-3,1)
6.将函数![]() 图象上的点P(1,0)平移至P′(2,0),则经过这种平移后得到的新
图象上的点P(1,0)平移至P′(2,0),则经过这种平移后得到的新
函数的解析式为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.为了得到![]() 的图象,可以把函数
的图象,可以把函数![]() 的图象按向量
的图象按向量![]() 进行平移,则
进行平移,则![]()
等于 ( )
A.(1,0) B.(-1,0) C.(![]() ) D.(
) D.(![]() )
)
8.已知![]() ,则△ABC一定是 ( )
,则△ABC一定是 ( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
9.若非零向量![]() 互相垂直,则下列各式中一定成立的是 ( )
互相垂直,则下列各式中一定成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.已知![]() ,且
,且![]() ,则
,则![]() 的夹角为 ( )
的夹角为 ( )
A.60° B.120° C.135° D.150°
11.已知O为原点,点A、B的坐标分别为(a,0),(0,a)其中常数a>0,点P在线段AB上,且![]() ,则
,则![]() 的最大值为 ( )
的最大值为 ( )
A.a B.2 a C.3 a D.a2
12.将椭圆![]() 按向量
按向量![]() 平移,使中心与原点重合,则
平移,使中心与原点重合,则![]() 的坐标为 ( )
的坐标为 ( )
A.(2,1) B.(-1,-2) C.(-1,2) D.(1,-2)
二、填空题(每小题4分,共16分,答案填在横线上)
13.将直线![]() 向右平移3个单位,再向下平移2个单位,所得直线与原来直线重合,则k=
.
向右平移3个单位,再向下平移2个单位,所得直线与原来直线重合,则k=
.
14.已知![]() 为单位向量,
为单位向量,![]() =4,
=4,![]() 的夹角为
的夹角为![]() ,则
,则![]() 方向上的投影为
.
方向上的投影为
.
15.已知![]() 的夹角为120°,且
的夹角为120°,且![]() ,
,![]() ,当
,当![]() 时,
时,
k= .
16.已知点A(-2,-3),B(-1,-6),C(19,4),则△ABC的形状是 .
三、解答题(本大题共74分,17—21题每题12分,22题14分)
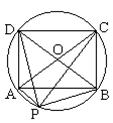
17.如图,矩形ABCD内接于半径为r的圆O,点P是圆周上任意一点,
|
18.平面内有向量![]() ,
,![]() ,点M为直线OP上一个动点.
,点M为直线OP上一个动点.
(1)当![]() 取最小值,求
取最小值,求![]() 的坐标;
的坐标;
(2)当点M满足(1)的条件和结论时,求![]() 的值.
的值.
19.设向量![]() 与向量
与向量![]() 的夹角为钝角,求实数t的取值范围.
的夹角为钝角,求实数t的取值范围.
20.已知△ABC的顶点坐标为A(1,2),B(2,3),C(3,1),把△ABC按向量![]() 平移后得到
平移后得到![]() ,若
,若![]() 的重心为G′(3,4)求△ABC的对应点A′、B′、C′以及
的重心为G′(3,4)求△ABC的对应点A′、B′、C′以及![]() 的坐标.
的坐标.
21.已知△ABC中,![]() ,若
,若![]() ,求证:△ABC为正三角形.
,求证:△ABC为正三角形.
22.已知抛物线C: ![]() .
.
(1)求抛物线顶点A的坐标;
(2)把A按![]() 平移,求对应点A′的坐标(
平移,求对应点A′的坐标(![]() );
);
(3)将已知抛物线C按![]() =(2,3)平移,得到抛物线C′,求C′的解析式;
=(2,3)平移,得到抛物线C′,求C′的解析式;
参考答案(11)
一、1.A 2.A 3.B 4.A 5.A 6.A 7.D 8.B 9.B 10.B 11.D 12.B
二、13.![]() 14.-2 15.
14.-2 15.![]() 16.直角三角形
16.直角三角形
三、17.![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
以上各式相加可证.
18.(1)设M(x,y),当y=2时,![]() 取最小值-8,此时
取最小值-8,此时![]() .
.
(2)![]() .
.
19.∵![]() ,故
,故![]() ,
,
解之![]() . 另有
. 另有![]() ,解之
,解之![]() ,
,
∴![]() .
.
20.![]() , A′=(2,4) , B′=(3,5) , C′=(4,3).
, A′=(2,4) , B′=(3,5) , C′=(4,3).
21.![]() ,
∴
,
∴![]() , 又∵
, 又∵![]() ,
, ![]() ,
,
故![]() , 知a=b, 同理可知b=c , 故a=b=c , 得证.
, 知a=b, 同理可知b=c , 故a=b=c , 得证.
22.(1)A(-1,2);
(2)A′(2,4);
(3)y=x2-2x+6.