高一三角同步练习6（化简与证明）

 高一三角同步练习6（化简与证明）

一、选择题

1、已知cosα= － ，α∈（π，2π），则tanα的值是　　　　（　）

A．　　B．　　C．　　D．±

2、化简的结果为　　　　　　 （　 ）

　 A．－cos160°　　B．cos160°　　C．±cos160°　　D．－sec160°

3、若是第二象限角，则化简的结果是　　 （　）

　 A．1　　 B．－1　　C．tan²α　　 D．－tan²α

4、若，则不可能是　　  （　 ）

　 A．第一、第二、第三象限角　　　 B．第一、第二、第四象限角

C．第一、第三、第四象限角　　　 D．第二、第三、第四象限角

5、如果角满足，那么的值是　　　　 （　）

　 A．　　  B．0　　　C．1　　　D．不存在

6、若为二象限角，且，那么是

  A．第一象限角 　B．第二象限角　　　　 C．第三象限角　　　　　　D．第四象限角

7、若, 则的值为：

  A．　　　　　　　　　　B．　　　　　　　　 C．　　　　　　　　　　　　　D．

8、函数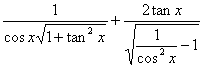值域中元素的个数是（　　）

A．1个　　　　　　　　　　　　　 B．2个　　　　　　　　 C．3个　　　　　　　　　　　 D．4个

二、填空题

1、化简sin²α＋sin²β－sin²αsin²β＋cos²αcos²β=　　　　　　　　　．

2、化简=　　　　　　　　　．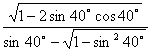

3、若是第四象限角，化简=________________．

4、若 = －2 tanα，则角的取值范围是　　　　　　　　 ．

三、解答题

1、化简：tanα（cosα－sinα）＋．

2、求证：．

3、求证：．

4、已知cosB = cosθsinA , cosC = sinθsinA ，求证：sin²A＋sin²B＋sin²C = 2．

参考答案

一、选择题

　　BABB　　DCDD

二、填空题

1、1；

2、-1；

3、；

4、

三、解答题

1、

2、左边

　　　 右边．

3、

∵

∴．

4、

∵，，

∴，

即：，

∴．