![]()
 高一年级第二学期数学期终考试试卷
高一年级第二学期数学期终考试试卷
一、填空题:(本大题共10小题,每小题4分,共40分)
1、函数![]() 的定义域为____________________(用区间表示)。
的定义域为____________________(用区间表示)。
2、函数![]() 的反函数是__________________。
的反函数是__________________。
3、方程![]() 的解是_____________________________。
的解是_____________________________。
4、化简: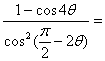 ____________________。
____________________。
5、函数![]() 的最小正周期是________________。
的最小正周期是________________。
6、等腰三角形ABC中,AB=AC,若![]() ,则cosA=__________________。
,则cosA=__________________。
7、关于x方程![]() 的解集为__________________。
的解集为__________________。
8、函数![]() 的单调递增区间是______________________。
的单调递增区间是______________________。
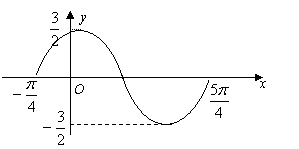 9、函数
9、函数![]() 其中
其中![]() 在一个周期内的图象如图所示,请根据图象,写出该函数的一个解析式:___________________。
在一个周期内的图象如图所示,请根据图象,写出该函数的一个解析式:___________________。
10、已知![]() ,则函数
,则函数![]() 的值域是_______。
的值域是_______。
二、选择题:(本大题共4小题,每小题4分,共16分)
11、已知![]() 的值是………………( )
的值是………………( )
![]()
![]()
![]()
![]()
12、要得到函数![]() 的图象,只要将函数
的图象,只要将函数![]() 的图象( )
的图象( )
A、向左平移![]() 个单位;
B、向右平移
个单位;
B、向右平移![]() 个单位;
个单位;
C、向左平移![]() 个单位;
D、向右平移
个单位;
D、向右平移![]() 个单位;
个单位;
13、方程![]() 的实根个数是………………………………( )
的实根个数是………………………………( )
A、0个; B、1个; C、2个; D、3个
14、已知函数![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 的值为……………………………( )
的值为……………………………( )
A、2 ; B、-2 ; C、3 ; D、-3
三、简答题:(本大题共4小题,每小题6分,共24分)
要求:写出解题过程,没有解题过程不得分。
15、指数函数![]() 在R上是增函数,求
在R上是增函数,求![]() 的取值范围。
的取值范围。
16、若![]() ,用a表示
,用a表示![]() 。
。
17、解关于![]() 的方程:
的方程:![]() 。
。
18、计算:已知![]() 是方程
是方程![]() 的两根,求
的两根,求![]() 的值。
的值。
四、解答题:(要求写出解题过程)
19、(本小题满分10分)
已知函数![]()
(1)将函数化为![]()
![]() 的形式;
的形式;
(2)当函数y取得最大值时,求自变量![]() 的集合。
的集合。
![]() 20、(本小题满分10分)
20、(本小题满分10分)
 三角形ABC中,三个内角A、B、C的对边分别为
三角形ABC中,三个内角A、B、C的对边分别为![]() ,若
,若![]() ,求角C的大小。
,求角C的大小。
高一数学期终考试试卷答案及评分标准
一、填空题:(本大题共10小题,每小题4分,共40分)
1、![]() ;
2、
;
2、![]() ;
;
3、![]() ;
4、2;
;
4、2;
5、![]() ;
6、
;
6、![]() ;
;
7、 ![]() ,
,
(也可以写成![]() );
);
8、![]() ;
;
9、![]() ;
10、
;
10、![]()
二、选择题:(本大题共4小题,每小题4分,共16分)
11、C; 12、A; 13、C; 14、A
三、简答题:(本大题共4小题,每小题6分,共24分)
要求:写出解题过程,没有解题过程不得分。
15、[解] ∵指数函数![]() 在R上是增函数,
在R上是增函数,
∴![]() ………………………………………………………(3分)
………………………………………………………(3分)
∴![]() 或
或![]() ……………………………………………(3分)
……………………………………………(3分)
16、〔解〕![]() ………………………………………(2分)
………………………………………(2分)
![]() ……………………………………………………(1分)
……………………………………………………(1分)
![]() ………………………………………………(1分)
………………………………………………(1分)
![]() …………………………………………………………(2分)
…………………………………………………………(2分)
17、〔解〕设![]() ,
,
则方程![]() 可以化为
可以化为![]() ,…………(2分)
,…………(2分)
∴![]() 。…………………………………………………(2分)
。…………………………………………………(2分)
∵y>0, ∴![]() 。…………………(2分)
。…………………(2分)
18、〔解〕∵![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ……………………………………(2分)
……………………………………(2分)
∴![]() …………………………………(2分)
…………………………………(2分)
∴![]() 。…………………………(2分)
。…………………………(2分)
四、解答题:(要求写出解题过程,本大题共20分)
19、(本小题满分10分)
〔解〕![]()
![]() ……………………………………(3分)
……………………………………(3分)
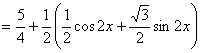
![]() …………………………………………………(3分)
…………………………………………………(3分)
当![]() ,即
,即![]() 时,…(2分)
时,…(2分)
![]() 。…………………………………………………(2分)
。…………………………………………………(2分)
20、(本小题满分10分)
[解]∵△ABC中,
![]()
∴由余弦定理:![]() 。…………………(2分)
。…………………(2分)
∴![]() ,∴
,∴![]() ,………………………………………(1分)
,………………………………………(1分)
∵![]() ,
,
∴由正弦定理:![]() ,…………………(2分)
,…………………(2分)
∴![]() ,……………………………………(1分)
,……………………………………(1分)
∴![]() ,…………………………………(2分)
,…………………………………(2分)
∴![]() 。…………………………………………………(2
。…………………………………………………(2