逻辑联结词·典型例题
能力素质
例1 下列语句中不是命题的是
[ ]
A.台湾是中国的
B.两军相遇勇者胜
C.上海是中国最大的城市
D.连接A、B两点
分析 “D”是描述性语句.
答 D.
例2 命题“方程x2-4=0的解是x=±2”中,使用的逻辑联结词的情况是
[ ]
A.没有使用联结词
B.使用了逻辑联结词“或”
C.使用了逻辑联结词“且”
D.使用了逻辑联结词“非”
分析 注意到x=±2是x=2或x=-2.
答 选B.
例3 命题①梯形不是平行四边形;②等腰三角形的底角相等;③有两个内角互补的四边形是梯形或圆内接四边形或是平行四边形;④60是5或2的公倍数,其中复合命题有
[ ]
A.①③④ B.③④
C.③ D.①③
分析 ②是简单命题,其余的均为复合命题.
解 选A.
![]()
作是“p或q”形式,p为________,q为________.
分析 “不超过”用“≤”表示,其否定是“>”,“≤”可以看作为“<”或“=”的复合形式.
![]()
说明:对命题的否定要“全面”,比如“>”的否定不是“<”.
例5 分别指出下列复合命题的形式及构成它的简单命题:
(1)4既是8的约数,也是12的约数;
(2)张明是数学课代表或英语课代数;
(3)江苏省不是中国面积最大的省.
分析 先寻找逻辑联结词,再确定被联结的简单命题.
解 (1)p且q,p:4是8的约数,q:4是12的约数;
(2)p或q,p:张明是数学课代表,q:张明是英语课代表;
(3)非p、p:江苏省是中国面积最大的省.
例6 以下判断正确的是
[ ]
A.若p是真命题,则“p且q”一定是真命题
B.命题“p且q”是真命题,则命题p一定是真命题
C.命题“p且q”是假命题时,命题p一定是假命题
D.命题p是假命题时,命题“p且q”不一定是假命题
解 根据真值表.选B.
说明:在记忆真值表的时候,要体会它的合理性.
例7 如果命题“p或q”与命题“非p”都是真命题,那么
[ ]
A.命题p不一定是假命题
B.命题q一定是真命题
C.命题q不一定是真命题
D.命题p与命题q的真值相同
分析 p为假,从而q为真.
解 选B.
例8 若p、q是两个简单命题,且“p或q”的否定是真命题,则必有
[ ]
A.p真q真 B.p假q假
C.p真q假 D.p假q真
分析 利用逆否命题与原命题的等价性,结合真值表确定结论.
解 ∵“p或q”的否定是“非p且非q”,这是一个真命题,所以由真值表.非p、非q都是真命题,那么p假q假.选B.
点击思维
例9 有下列五个命题
(1)40能被3或5整除;
(2)不存在实数x,使x2+x+1<0;
(3)对任意实数x,均有x+1>x;
(4)方程x2-2x+3=0有两个不等的实根;
![]()
其中假命题为________.(只填序号)
分析 使用不同的方法分别验证.
答 填写(4).
例10 p:菱形的对角线互相垂直.q:菱形的对角线互相平分.求下列复合命题:
(1)p或q (2)p且q (3)非p
分析 一般的问题都是“拆”复合命题,这儿是“造”复合命题,关键在于“合”.
解 (1)菱形的对角线互相垂直或平分;
(2)菱形的对角线互相垂直且平分;
(3)菱形的对角线互相不垂直.
例11 以1表示真,以0表示假,填写下面的真值表.
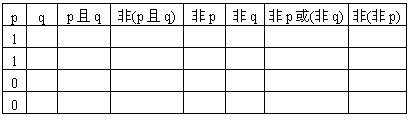
分析 将q的可能取值与p对应,然后依真值表逐格填写.
解
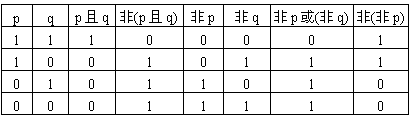
说明:有时需要我们综合应用真值表.
例12 分别指出下列各组命题构成的“p或q”、“p且q”、“非p”形式的复合命题的真假.
![]()
(2)p:4>6.q:4+6≠10.
分析 利用真值表.
解 (1)p或q:真;p且q:真;非p:假.
(2)p或q:假;p且q:假;非p:真.
说明:本题是要求先“造”命题,然后判定其真假.
例13 如果命题“p或q”是真命题,“非p”是假命题,那么
[ ]
A.命题p一定是假命题
B.命题q一定是假命题
C.命题q一定是真命题
D.命题q是真命题或者假命题
分析 利用真值表回推.
答 选D.
说明:解题过程中注意发挥逆向思维的作用.
学科渗透
例14 命题“非空集合A∩B中的元素既是A中的元素也是B中元素”是________形式.命题“非空集合A∪B中的元素是A的元素或是B的元素”是________形式.
分析 x∈A∩B则x∈A且x∈B,填p且q.
x∈A∪B则x∈A或x∈B.填p或q.
答 填p且q;p或q.
说明:本题是集合问题与命题概念的结合.
例15 分别指出下列各命题的形式及构
成它的简单命题,并指出复合命题的真假.
(1)8或6是30的约数;
(2)矩形的对角线垂直平分;
(3)方程x2-2x+3=0没有实数根.
分析 分清形式结构,判断简单命题真假,利用真值表再判断原复合命题真假.
解 (1)p或q,p:8是30的约数(假),q:6是30的约数(真).“q或q”为真.
(2)p且q,p:矩形的对角线互相垂直(假),q:矩形的对角线互相平分(真).“p且q”为假.
(3)非p、p:x2-2x+3=0有实根(假).非p为真.
说明:将简易逻辑知识负载在其他知识之上