北大附中高一年级下学期数学期中考试
班级:______ 姓名:______ 成绩:_______
一、选择题:
在下列各题的四个被选答案中,只有一个是正确的,请你将正确答案前的字母添在答题卡中。(每题3分,共36分)
1.求值![]() ( )
( )
(A) ![]()
(B) ![]()
(C) ![]()
(D)![]()
2.把曲线y=sinx向右平移![]() 个单位,再把各点横坐标缩短到原来的
个单位,再把各点横坐标缩短到原来的![]() ,所得的图像的函数式是( )
,所得的图像的函数式是( )
(A)![]()
(B)![]()
(C) ![]()
(D)![]()
3.函数y=Asin (ωx+φ)在同一周期内,
当![]() 时,有最大值
时,有最大值![]() ,
,
当![]() 时,有最小值-
时,有最小值-![]() ,
,
则函数的解析式为( )。
(A)![]()
(B)![]()
(C)![]()
(D)![]()
4. 当![]() 时,使函数
时,使函数![]() 取得最大值的x的集合是( )
取得最大值的x的集合是( )
(A)![]()
(B)![]()
(C)![]()
(D)以上答案都不正确
5. 已知![]() ,则
,则![]() 的值是( )
的值是( )
(A)![]() 和
和 ![]()
(B) ![]() 和
和![]()
(C)![]()
(D)![]()
6.如果![]() 成立,则a的取值范围是( )
成立,则a的取值范围是( )
(A)a=10 (B) a>1
(C)0<a<1 (D)a>2
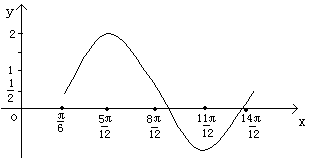
7. 如图,是周期为2π的三角函数y=f(x)的图象,那么f(x)可以写成( )。
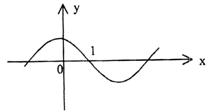
(A)sin (1-x) (B)cos (1-x)
(C)sin (x-1) (D)cos (x-1)
8.已知正四棱柱![]() 底面边长为1,侧棱长为2,E为
底面边长为1,侧棱长为2,E为![]() 的中点,则异面直线
的中点,则异面直线![]() 与
与![]() 所成角的余弦值为
( )
所成角的余弦值为
( )
(A)![]() (B)
(B)
![]()
(C)![]() (D)0
(D)0
9.正四棱台的上底面面积为2,中截面面积为4,则下底边长为( )
(A)![]() (B)
(B) ![]()
(C)![]() (D)
(D)![]()
10. 正四棱台的两个相邻侧面所成的二面角的平面角一定是( )
(A)锐角 (B)直角
(C)钝角 (D)不能确定
11.正六棱柱底面边长为2,最长的一条对角线长为![]() ,则它的全面积为( )
,则它的全面积为( )
(A)![]()
(B)![]()
(C)![]()
(D)![]()
12 . 正四面体ABCD 的棱长为a, E、F、G分别是棱AB、AC、CD的中点,截面EFG交棱BD于H,则点A到截面EFGH的距离是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
二、填空题(每空3分,共12分)
13.一个正六棱台的斜高为![]() ,两底面边长差为10cm,它的全面积为
,两底面边长差为10cm,它的全面积为![]() ,那么它的两底面边长分别为_________。
,那么它的两底面边长分别为_________。
14.若函数f(x)是周期为5的偶数,且f(2)=-3,则![]() 的值是_________,
的值是_________,![]() 的值是_________.
的值是_________.
15.函数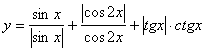 的定义域是_______,值域是__________。
的定义域是_______,值域是__________。
16. 如图所示的几何体,是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的,现用一个平面去截这个几何体,若这个平面垂直于圆柱底面所在的平面,那么截得的图形可能是图①②③④中的________(把可能的图的序号都填号)
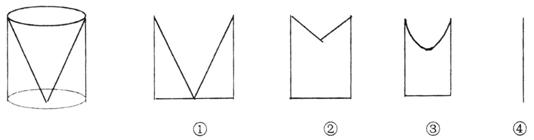
三、解答题:
17.已知![]() ,求
,求![]() 的值。
的值。
18.求证:![]()
19 . 已知![]() ,
,
求证:![]()
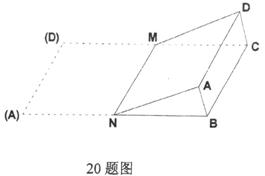
20.平行四边形ABCD中,∠A=60°,AD=a,AB=2a,,M、N分别是CD、AB的中点,以MN为轴,将四边形ADMN沿MN翻折,当二面角A—MN—B为60°时,求三棱柱ABN—CDM的侧面积。
21.作出函数![]() 的简图,并说明它是由正弦曲线y=sinx经过怎样的变化而得到的。
的简图,并说明它是由正弦曲线y=sinx经过怎样的变化而得到的。
22.已知关于x的方程![]() 的两根为
的两根为![]() 和
和![]() ,
,![]() 。
。
求(1)![]() 的值;
的值;
(2)m的值;
(3)方程的两个根及此时的θ值。
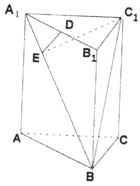
23.如图,在直三棱柱![]() 中,AC=BC=1,∠ACB=90°,
中,AC=BC=1,∠ACB=90°,![]() ,D是
,D是![]() 中点,过D作
中点,过D作![]() ,垂足为E。
,垂足为E。
(1)求证:![]() ;
;
(2)平面ABC与平面![]() 所成二面角的正切值;
所成二面角的正切值;
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。
北大附中高一年级下学期数学期中考试
参考答案
一、
1.B 2.A 3.C 4.B 5.A 6.C 7.A 8.C 9.C 10.C 11.B 12.D
二、
13.4,14
14.![]() ,
,![]() 。
。
15.![]()
![]()
16.①、③、④
三、
17.
解∵![]()
∴![]()
∴原式![]()
![]()
![]()
![]()
18.
证:左边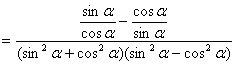

∴原等式成立
19.
证:由![]()
得![]()
两边同除以![]() (
(![]() ,
,![]() 时此题不考虑)得
时此题不考虑)得
![]() ,
,
∴![]()
![]() ,
,
∴![]()
∴![]()
原等式成立。
20.
解:在平行四边形ABCD中,
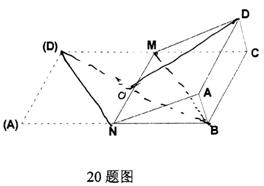
连结BD交MN于O。
连接DN,BM,∵AB=2AD, ∴AD=AN。
又∠A=60°∴△AND为正三角形
∴DN=AD=BN, ∴BNDM为菱形。
∴BD⊥MN,折叠后,必有BO⊥MN,
DO⊥MN,∴∠DOB为二面角A-MN-B的平面角,
∴∠BOD=60°
在△ODM中∠DOM=90°,DM=a,∠DMO=60°
∴![]() 。
。
∴在正三角形OBD中,![]()
又MN⊥平面OBD,∴MN⊥BD,
而![]() ,∴BC⊥BD,∠DBC=90°。
,∴BC⊥BD,∠DBC=90°。
BC=a ∴![]() ,
,
∴![]() 。
。
∴![]()
∴![]()
21.
| x |
|
|
|
|
|
|
| 0 |
| π |
| 2π |
| y |
| 2 |
| -1 |
|
把曲线y=sinx上各点的横坐标压缩到原来的![]() ,
,
然后把曲线向右平移![]() ,再把各点的纵坐标扩大到原来的
,再把各点的纵坐标扩大到原来的![]() 倍,
倍,
最后把曲线向上平移![]() 个单位,得
个单位,得![]() 图象
图象
22.
解:由已知得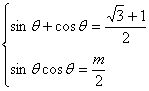
(1)原式![]()
![]()
(2)∵![]() ,
,
∴![]()
即![]()
∴ ![]() 。
。
(3)当![]() 时,原方程为
时,原方程为![]()
即![]() ,即
,即![]() 或
或![]()
∴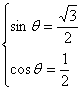 或
或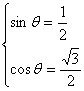
∵θ∈(0,2π)
∴![]() 或
或![]()
23.(1)证:在直棱柱![]() 中,∵AC=BC,
中,∵AC=BC,
∴![]() ,连
,连![]() ,∵D是
,∵D是![]() 中点。
中点。
∴![]() ,又∵平面
,又∵平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,于是DE是
,于是DE是![]() 在平面
在平面![]() 上的射影,
上的射影,
又∵![]() ,∴
,∴![]() 。
。
(2)∵上、下底面平行,
∴平面ABC与平面![]() 所成的二面角就是二面角
所成的二面角就是二面角![]()
∵![]() 底面
底面![]() ,
,![]() 。
。
∴![]() ,于是
,于是![]() 即为所求二面角的平面角。
即为所求二面角的平面角。
在![]() 中,
中,![]() 。
。
(3)作![]() 垂足为F,∵
垂足为F,∵![]() 平面
平面![]() ,∴
,∴![]() 。
。
又∵![]() ,∴
,∴![]() 平面
平面![]()
∴![]() 的长,即为点
的长,即为点![]() 到平面
到平面![]() 的距离。
的距离。
在![]() 中,
中,![]() ,∴
,∴![]() ,
,
∴点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。