邵阳市一中2005年下学期期末复习
高一数学测试试题卷
时量 120分钟 满分 120分
一、选择题(将唯一正确的答案代号填到答题卷上,每题4分,共40分)
1.设集合![]() ,则下列关系式中正确的是
,则下列关系式中正确的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.集合 M=![]() ,
,![]() ,则
,则![]() =
=
A.Φ![]() B.(0,+∞) C.[0,+∞) D.R
B.(0,+∞) C.[0,+∞) D.R
3.定义![]() ,若
,若![]() ,
,![]() ,
,
则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.一元二次方程![]() 有一个正根和一个负根的一个充分不必要条件是
有一个正根和一个负根的一个充分不必要条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知命题甲:![]() 或
或![]() ,命题乙:
,命题乙:![]() 。则甲是乙的
。则甲是乙的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.函数![]() 的递减区间为
的递减区间为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.等差数列共有![]() 项,所有奇数项之和为132,所有偶数项之和为121,
项,所有奇数项之和为132,所有偶数项之和为121,
则n=
A.9 B.10 C.11 D.12
8.各项均为正数的等比数列![]() 中,若
中,若![]() 0,则
0,则![]()
A.9 B.10 C.11 D.12
9.数列![]() 的前
的前![]() 项之和为
项之和为![]() ,则
,则![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.要得到函数![]() +2的图象,只须将函数
+2的图象,只须将函数![]() 的图象
的图象
A.向左移动1个单位再向下移动2个单位
B.向左移动1个单位再向上移动2个单位
C.向右移动1个单位再向下移动2个单位
D.向右移动1个单位再向上移动2个单位
二、填空题(每题4分,共20分)
11.已知数列![]() 的前n项和
的前n项和![]() ,若
,若![]() 是等比数列,则
是等比数列,则![]() = .
= .
12.设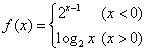 ,则
,则![]() =________
=________
13.设函数![]() ,
,
则![]() _______.
_______.
14.电子技术飞速发展,计算机的成本不断降低,若每隔3年计算机的价格降低![]() ,则现在价格为6750元的计算机经过9年后价格应为_________元.
,则现在价格为6750元的计算机经过9年后价格应为_________元.
15.设等比数列![]() 的公比为q,前n项和为Sn,若
的公比为q,前n项和为Sn,若![]() 、
、![]() 、
、![]() 成等差数列,则q的值为 .
成等差数列,则q的值为 .
三、解答题(每题10分,共60分)
16.已知函数![]()
(Ⅰ) 证明f(x)是减函数;
(Ⅱ) 求函数![]() 的反函数
的反函数![]() .
.
17.已知不等式 ![]() ≤1对
≤1对![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
18.有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q
(万元),它们与投入资金![]() (万元)的关系为:
(万元)的关系为:
![]() , Q
, Q![]() 。今有3万元资金投入经营甲、乙两种商品,对甲、乙
。今有3万元资金投入经营甲、乙两种商品,对甲、乙
两种商品的资金投入分别为多少时,所获利润最大?最大利润是多少?
19.函数![]() 在区间
在区间![]() 上递减,求
上递减,求![]() 的取值范围。
的取值范围。
20.已知各项均为正数的等比数列![]() 的项数为偶数,它的所有项之和等于
的项数为偶数,它的所有项之和等于
它的偶数项之和的4倍,且![]() .
.
(Ⅰ) 求首项![]() 和公比
和公比![]() ;
;
(Ⅱ) 若数列![]() 的前
的前![]() 项之和最大,求
项之和最大,求![]() .
.
21.数列{an}的前n项和为Sn,且a1=1,![]() ,n=1,2,3,……,求
,n=1,2,3,……,求
(Ⅰ) a2,a3,a4的值及数列{an}的通项公式;
(Ⅱ) ![]() 的值.
的值.
高一数学参考答案
一、CBBCB,ADCAD
二、11.![]() 12.
12.![]() 13.100
14.2000
15.
13.100
14.2000
15.![]()
三、16. (Ⅰ) 设![]() ,则
,则![]() ………………………2分
………………………2分
∴![]()
![]() …………4分
…………4分
即 ![]() ,所以
,所以![]() 是减函数。
…………………………5分
是减函数。
…………………………5分
(Ⅱ) ∵![]() …………………………………………6分
…………………………………………6分
∴![]() ………………………………………………8分
………………………………………………8分
所以函数![]() 的反函数
的反函数![]() =
=![]() ………………10分
………………10分
17.∵![]() 恒成立,……………………………………………2分
恒成立,……………………………………………2分
∴![]() ≤1恒成立
≤1恒成立![]() 恒成立…3分
恒成立…3分
![]() ……………………………………………5分
……………………………………………5分
![]() …………………………………………8分
…………………………………………8分
即![]() ,解得
,解得![]() ………………………………………10分
………………………………………10分
18. 设投入经营乙种商品![]() 万元,则投入甲种商品的资金为
万元,则投入甲种商品的资金为![]() 万元,
万元,
经营两种商品的利润总额为![]() (万元),……………………………3分
(万元),……………………………3分
则 ![]()
![]()
![]() ………………………………………………5分
………………………………………………5分
=![]() ……………………………………………………7分
……………………………………………………7分
∴当![]() ,即
,即![]() 时,
时,![]() 有最大值
有最大值![]() (万元 ………8分
(万元 ………8分
故对甲乙两种商品的资金分别投入0.75万元和2.25万元时,
所获利润最大,最大利润为1.05万元。………………………………10分
19. 设![]() ,则
,则![]() 在区间
在区间![]() 上递减
上递减
![]()
![]() 在区间
在区间![]() 上递增,且
上递增,且![]() 在区间
在区间![]() 上恒为正 ……5分
上恒为正 ……5分
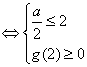 ………………………………………………………………8分
………………………………………………………………8分
解得 ![]() ……………………………………………………………10分
……………………………………………………………10分
20. (Ⅰ)设数列共有![]() 项,由已知条件可得
项,由已知条件可得

解得 ![]() ……………………………………………………5分
……………………………………………………5分
(Ⅱ) 由(Ⅰ)可知:![]() ,
,
令![]() ,则数列
,则数列![]() 是首项为
是首项为![]()
公差为![]() 的等差数列. …………………………………………7分
的等差数列. …………………………………………7分
要使其前![]() 项之和最大,必须且只须
项之和最大,必须且只须
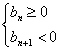
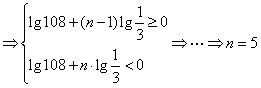 ………………………10分
………………………10分
21. (I)由a1=1,![]() ,n=1,2,3,……,得
,n=1,2,3,……,得
![]() ,
,![]() ,
,
![]() ,…………………………………………3分
,…………………………………………3分
由![]() (n≥2),得
(n≥2),得![]() (n≥2),…………5分
(n≥2),…………5分
又a2=![]() ,所以an=
,所以an=![]() (n≥2),
(n≥2),
∴ 数列{an}的通项公式为![]() ;………………………7分
;………………………7分
(II)由(I)可知![]() 是首项为3,公比为16,项数为n的等比数列,∴
是首项为3,公比为16,项数为n的等比数列,∴ ![]() =
=![]() .………………………………10分
.………………………………10分