徽州一中2002—2003学年度高一数学单元测验（集合与函数）
班级 姓名 得分
一、选择题（每小题3分，共36分）
1．
若A=
，则集合A中元素个数为
（A）1个， （B）2个， （C）3个， （D）4个。
2．设
全集U=R，则[UA等于
（A）
（B）
（C）
（D）
3．若集合P
则满足条件的集合P的个数为 （ ）
(A) 6； (B) 7； (C) 8； (D) 1。
4．下列命题：（1）3≥3；（2）∣x∣≤x；(3)－2≤－2；(4) ∣x∣≥－x；其中真命题的个数为（ ）
（A）1； （B）2； （C）3； （D）4
5．已知P：∣2x－3∣>1；q:
；则﹁p是﹁q的（ ）条件。
（A）充分不必要条件； （B）必要不充分条件；
（C）充分必要条件； （D）既非充分条件又非必要条件。
6．函数f(x)
是偶函数，则下列各点中必在y=f(x)图象上的是
（A）
（B）
（C）
（D）
。
7．
的一个必要不充分条件是（ ）
（A）
；（B）
； （C）
（D）
8．如果命题“P或Q”是真命题，命题“P且Q”是假命题，，那么
(A) 命题P和命题Q都是假命题； (B) 命题P和命题Q都是真命题；
(C) 命题P和命题“非Q”真值不同； (D) 命题Q和命题“非P”真值相同；
9．函数
的单调递减区间是
(A) 
；(B) 
； (C) 
； (D) 
10．函数
是定义在R上的增函数，且
，则下列三个值：
，
，
的大小关系是
A．
； B．
； C．
； D．
.
11．若函数满足
，且
，则
的值为
（A）
；（B）
；（C）
；（D）
12．定义在区间
的奇函数f(x)为增函数，偶函数g(x)在
的图像与f(x)的图像重合，设
，给出下列不等式
①
②
③
④
其中成立的是
（A) ①与④ ； (B) ②与 ③ ； (C) ① 与 ③ ； (D) ②与 ④。
答 题 栏
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二．填空题（每小题4分，共16分）
13．设f(x)=5-g(x)，且g(x)为奇函数，已知f（-5)=-5,则f(5)的值为 。
14．函数
（x≤1）反函数为
。
15．函数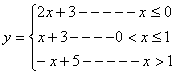
；的最大值是
。
16．对于定义在R上的函数f(x)，若实数
满足f()=，则称是函数f(x)的一个不动点.若函数f(x)=
没有不动点，则实数a的取值范围是
。
三．解答题（共48分）
17．一次函数f(x)=
(1)若f(x)是减函数，且f(1)=0,求m的值；
(2)若f(x)是奇函数，求m的值。
18．已知函数y=f(x)在定义域
内存在反函数，且
，求
的值。
19．已知
，且
其中k是常数，求证：①
；②
。
20．已知
。
。
21．如图。以墙为一边，用篱笆围成长方形的场地，并用平行于一边的篱笆隔开，已知篱笆的总长为定值L，这块场地的长和宽各为多少时，场地的面积最大？最大面积是多少？
