扬州大学附属中学
高一数学练习(十二月)
班级____ 姓名____ 学号____ 成绩____
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
1.
如果三点(3,5),(m,7),(-1,2)在一条直线上,则![]() = ( )
= ( )
A.![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 如果把两条异面直线看成“一对”,那么六棱锥的棱所在的12条直线中,异面直线共有( )
A.12对 B.24对 C.36对 D.48对
3. 长方体的三个面的面积分别为2、6和9,则长方体的体积为( D )
A.7
B.8 C.![]() D.
D.![]()
4. 函数![]() 的图象关于
( )对称
的图象关于
( )对称
A. ![]() 轴 B.
轴 B.![]() 轴 C. 原点 D.直线
轴 C. 原点 D.直线![]()
5. 设正三棱柱的外接圆柱体体积为V1,内切圆柱体积为V2,则( )
A.V1∶V2=1∶1 B.V1∶V2=2∶1
C.V1∶V2=4∶1 D.V1∶V2=8∶1
6. 过点![]() 的直线中,被
的直线中,被![]() 截得的最长弦所在的直线方程是( )
截得的最长弦所在的直线方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7. 下列函数中,值域是![]() 的是
( )
的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. 如果直线![]() 将圆
将圆![]() 平分,且不通过第四象限,则直线
平分,且不通过第四象限,则直线![]() 的斜率的取值范围是( )
的斜率的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
9. 已知![]() 是四条不重合的直线,其中
是四条不重合的直线,其中![]() 为
为![]() 在平面
在平面![]() 上的射影,
上的射影,![]() 为
为![]() 在平面
在平面![]() 上的射影,则(
)
上的射影,则(
)
A.![]()
![]()
![]() B.
B.![]()
![]()
![]()
C.![]()
![]()
![]() D.
D.![]()
![]()
![]()
10. 已知函数 ![]() ,
, ![]() 且
且 ![]() 则
( )
则
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11. 设点![]() 是函数
是函数![]() 图象上任一点,则
图象上任一点,则![]() 的取值范围是( )
的取值范围是( )
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
![]() .
.![]()
12. 直线![]() :
:![]() 与圆C:
与圆C:![]() 有两个交点A、B,且以AB为直径的圆过坐标原点, 则
有两个交点A、B,且以AB为直径的圆过坐标原点, 则![]() 的值是 ( )
的值是 ( )
A.2
B.3
C.-1
D.![]()
二、填空题:
13. 直线l过原点且与直线![]() x-y-4=0的夹角是
x-y-4=0的夹角是![]() , 则直线l的方程是_____.
, 则直线l的方程是_____.
14. 若实数![]() 满足
满足![]() ,则
,则![]() 的最小值是______.
的最小值是______.
15. 异面直线![]() 所成的角为
所成的角为![]() ,直线
,直线![]() 与
与![]() 所成的角都等于
所成的角都等于![]() ,则
,则![]() 的取值范围是___________.
的取值范围是___________.
16. 已知直线![]() :
:![]() ,曲线C:
,曲线C:![]() 有两个公共点,则
有两个公共点,则![]() 的取值范围是___________.
的取值范围是___________.
三、解答题:
17. 如图是一个有盖圆台形储油桶,其上底半径是30cm,下底半径是60cm,大约能储存264(约为![]() )升油,问造这样的油桶约需多少平方米材料(接缝忽略不计,精确到0.01平方米)?
)升油,问造这样的油桶约需多少平方米材料(接缝忽略不计,精确到0.01平方米)?
18. 已知△ABC的顶点为A(2,4),B(1,-2),C(-2,3)。
(Ⅰ)求BC边上的中线AM所在直线的方程;
(Ⅱ)求△ABC的面积。
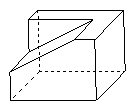
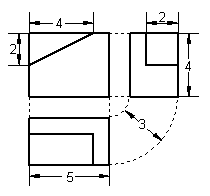
19. 一个几何体的直观图和三视图如图所示,求此几何体的表面积和体积.
20. 已知圆C:![]() ,直线
,直线![]() :
:![]() 。
。
(Ⅰ)求证:对![]() ,直线
,直线![]() 与圆C总有两个不同交点;
与圆C总有两个不同交点;
(Ⅱ)设![]() 与圆C交于不同两点A、B,若
与圆C交于不同两点A、B,若![]() ,求
,求![]() 的倾斜角;
的倾斜角;
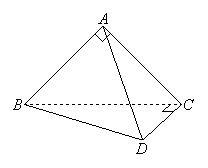
21. 如图,△ABC与△BCD是一副三角板,它们所在的两个平面互相垂直.若AB=AC,∠BAC=∠BCD=90°,∠CBD=30°。
(Ⅰ)求证:三棱锥A-BCD的四个面都是直角三角形;
(Ⅱ)求二面角A-BD-C的正切值。
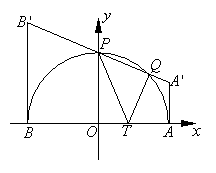
22. 已知点T是半圆O的直径AB上一点,AB=2、OT![]() ,以AB为直腰作直角梯形
,以AB为直腰作直角梯形![]() ,使
,使![]() 垂直且等于AT,使
垂直且等于AT,使![]() 垂直且等于BT,
垂直且等于BT,![]() 交半圆于P、Q两点,建立如图所示的直角坐标系 .
交半圆于P、Q两点,建立如图所示的直角坐标系 .
(Ⅰ)写出直线![]() 的方程;
的方程;
(Ⅱ)计算出点P、Q的坐标;
(Ⅲ)证明:沿PT射出的光线,经AB反射后,反射光线通过点Q.