南昌市2001—2002学年度第一学期期末终结性测试卷
高一数学
一、选择题(本大题共10小题,每小题3分,共30分)
1、计算![]() 的结果为( )
的结果为( )![]()
(A)![]() (B)-
(B)-![]() (C)
(C)![]() (D)-
(D)-![]()
2、若![]() 等于( )
等于( )
(A)1 (B)2 (C)3 (D)6
3、在等差数列![]() 中,已知
中,已知![]() ,则前5项之和等于( )
,则前5项之和等于( )
(A)32 (B)20 (C)16 (D)10
4、数列![]() 的通项公式
的通项公式![]() ,则其前n项和的公式为( )
,则其前n项和的公式为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
5、若函数![]() 的定义域是(-∞,0),则a的取值范围是( )
的定义域是(-∞,0),则a的取值范围是( )
(A)(-∞,0) (B)(1,+∞) (C)(0,1) (D)(0,1)∪(1,+∞)
6、已知公差不为零的等差数列第4,7,16项,恰是等比数列的4,6,8项,则该等比数列的公比是( )
(A)![]() (B)
(B)![]() (C)±
(C)±
![]() (D)±
(D)±![]()
7、已知等比数列的公比为2,且前4项和为1,那么前8项之和等于( )
(A)15 (B)17 (C)19 (D)21
8、在各项为正数的等比数列![]() 中,若
中,若![]() ( )
( )
(A)12 (B)11 (C)8 (D)10
9、函数![]() 的值域是( )
的值域是( )
(A)![]() (B)R (C)
(B)R (C)![]() (D)
(D)![]()
10、各项均为实数的等比数列![]() 的前n项和记为
的前n项和记为![]() 等于( )
等于( )
(A)150 (B)-200 (C)150或-50 (D)100
二、填空题(本题共5小题,每小题4分,共20分)
11、方程![]() 的根的个数是
个.
的根的个数是
个.
12、在等比数列![]() 中,若
中,若![]() ,
,![]() 则
则![]() =
.
=
.
13、![]() = .
= .
14、已知函数![]() 的值域为
的值域为![]() ,那么函数f(x)的定义域是
.
,那么函数f(x)的定义域是
.
15、已知等差数列{![]() }中,
}中,![]() 若m>1,且
若m>1,且![]() ,则m= .
,则m= .
三、解答题(本题共5小题,共50分),解答应写出文字说明、演算步骤或证明过程
16、(本题分2小题,每小题5分,共10分)
(1)![]()
(2)已知:![]() ,试用a、b表示
,试用a、b表示![]() .
.
17、(本题8分)已知数列![]() 的前3项依次为1,2,3.它的前n项和为
的前3项依次为1,2,3.它的前n项和为![]() ,试求数列的通项
,试求数列的通项![]() .
.
18、(本题10分)设数列![]() 为等差数列,
为等差数列,![]() 为数列
为数列![]() 的前n项和,已知
的前n项和,已知![]() 为数列
为数列![]() 的前n项和,求
的前n项和,求![]() .
.
19、(本题10分)已知函数![]()
![]()
(1)求函数![]() 的定义域和值域;
的定义域和值域;
(2)求函数![]() 的反函数.
的反函数.
20、(本题12分)已知等差数列![]() ,满足
,满足![]() 且
且
(1)求数列![]() 的通项公式.
的通项公式.
(2)把数列![]() 的第1项、第4项、第7项、……、第3n-2项……分别作为数列
的第1项、第4项、第7项、……、第3n-2项……分别作为数列![]() 的第1项、第2项、第3项、……、第n项……,求数列
的第1项、第2项、第3项、……、第n项……,求数列![]() 的前n项和
的前n项和![]() .
.
参考答案及评分意见:
一、C B D D C C B D A A
二、11、0; 12、![]() ;
;
13、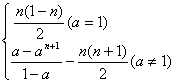
14、[-4,-2]∪[2,4]; 15、10.
三、16、(1)解:原式=![]() ……2分
……2分
![]() ………………5分
………………5分
(2)解:由已知可得![]() .……………………2分
.……………………2分
![]() ………………5分
………………5分
17、解:
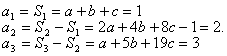
解得 ![]() ………………4分
………………4分
![]() ………………5分
………………5分
![]() ……………………8分
……………………8分
18、解:设等差数列![]() 的公差为d,则
的公差为d,则![]() ………2分
………2分
![]()
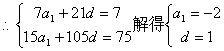 ………………5分
………………5分
![]()
![]() ∴数列
∴数列![]() 是等差数列,
是等差数列,
其首项为-2,公差为![]() ………………8分
………………8分
![]() ………………10分
………………10分
19、解:(1)![]() …………2分
…………2分
当0<a<1时,由![]() ∴x>0
∴x>0
由![]() 得
得
![]()
∴当0<a<1时,函数f(x)的定义域是(0,+∞),值域是(0,+∞)…………4分
当a>1时,由![]() 得x<0
得x<0
由![]()
∴当a>1时,函数f(x)的定义域是(-∞,0),值域是(-∞,0)…………6分
(2)设![]()
![]() …………8分
…………8分
∴![]() ………………10分
………………10分
20、(1)![]() 为等差数列
为等差数列![]() ,又
,又![]()
解方程![]()
![]() ………………3分
………………3分
公差![]() ………………6分
………………6分
(2)![]() ……………9分
……………9分
![]()
![]() 是首项为2,公比为
是首项为2,公比为![]() 的等比数列.
的等比数列.
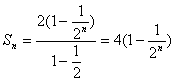 …………………………12分
…………………………12分