高2008第一学期期末数学模拟试卷(四)
一、选择题(本大题共12小题,每小题5分,共60分)
1、由实数![]() 所组成的集合中,元素的个数为( )
所组成的集合中,元素的个数为( )
A、1个或2个 B、1个或3个 C、2个或3个 D、1个,2个或3个
2、设全集![]() ,则
,则![]() 的值为( )
的值为( )
A、3
B、9
C、![]() D、3或9
D、3或9
3、![]() 是
是![]() 的( )
的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
4、已知![]() 是一个等比数列的前三项,则第四项是( )
是一个等比数列的前三项,则第四项是( )
A、
![]() B、
B、![]() C、13.5
D、12
C、13.5
D、12
5、数列![]() 的一个通项公式是( )
的一个通项公式是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6、设![]() 是函数
是函数![]() 的反函数,则以下不等式中恒成立的是( )
的反函数,则以下不等式中恒成立的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
7、已知![]() ,则
,则![]() =( )
=( )
A、4 B、5 C、6 D、7
8、在等比数列![]() 中,
中,![]() ,则
,则![]() ( )
( )
A、![]() B、
B、 ![]() C、
C、![]() D、
D、![]()
9、![]() ,命题
,命题![]() ,若“q”是真命题且“p且q”是假命题,则满足条件的
,若“q”是真命题且“p且q”是假命题,则满足条件的![]() 是( )
是( )
A、![]() B、
B、![]() C、x=-2,-1-0,1,2。 D、x=-1,0,1
C、x=-2,-1-0,1,2。 D、x=-1,0,1
10、不等式![]() 的解集是( )
的解集是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、已知函数![]() 是R上的增函数,A(0,-1)、B(3,1)是其图象上的两点,则
是R上的增函数,A(0,-1)、B(3,1)是其图象上的两点,则![]() 的解集是( )
的解集是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
12、和是![]() ,则当n>2时,下列不等式中的是( )
,则当n>2时,下列不等式中的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
二、填空题(本大题共4小题,每小题4分,共16分)
13、函数![]() 的单调递减区间是
。
的单调递减区间是
。
14、
已知数列![]() 中,
中,![]() 又是数列
又是数列![]() 等比数列则
等比数列则![]() 。
。
15、要使函数![]() 有反函数,则a的最大值是
。
有反函数,则a的最大值是
。
16、 给出下列函数:
①
函数![]() 与函数
与函数![]() 的定义域相同;
的定义域相同;
②
函数![]() 与函数
与函数![]() 值域相同;
值域相同;
③
函数![]() 与函数
与函数![]() 在
在![]() 上都是增函数;
上都是增函数;
④
函数![]() 的定义域是
的定义域是![]() 。其中错误的序号是
。
。其中错误的序号是
。
三、解答题(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤)
17、(本小题12分)已知全集U=R,集合A=![]() ,集合B=
,集合B=![]() ,求
,求![]() 和
和![]() 。
。
18、
本小题12分)已知函数![]() 。(1)若不等式
。(1)若不等式![]() 的解集是
(1,3),求不等式
的解集是
(1,3),求不等式![]() 的解集;(2)若
的解集;(2)若![]() ,证明
,证明![]() 在(0,
在(0,![]() 上是单调递减函数。
上是单调递减函数。
19、(本小题12分)等比数列![]() 同时满足下列三个条件:①
同时满足下列三个条件:①![]() ;②
;②![]() ;③三个数
;③三个数![]() 依次成等差数列,求数列
依次成等差数列,求数列![]() 的通项公式及前n项和
的通项公式及前n项和![]() 。
。
20、(本小题12分)已知函数![]() 的图象过点
的图象过点![]() 和
和![]() ,
,
①
求函数![]() 的解析式;② 函数
的解析式;② 函数![]() 的反函数;③设
的反函数;③设![]() 是正整数,是数列的前项和
是正整数,是数列的前项和![]() ,解关于的不等式
,解关于的不等式![]() 。
。
21、(本小题满分12分)某市2003年共有1万两燃油型公交车,有关部门计划于2004年投入128辆电力公交车,随后电力公交车每年的投入比上年增加,试问:
(1)该市在2010年应该投入多少辆电力公交车;(2)哪一年底,电力公交车的数量开始超过该市公交车总量的![]() ? (参考数据:
? (参考数据:![]() )
)
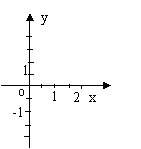 22、(本小题满分14分)已知函数
22、(本小题满分14分)已知函数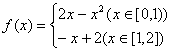 。(1)在所给坐标系中,画出
。(1)在所给坐标系中,画出![]() 的图象;(2)设
的图象;(2)设![]() ,
,![]() 的反函数为
的反函数为![]() ,设
,设![]() ,求数列
,求数列![]() 的通项公式;(3)若
的通项公式;(3)若![]() ,求
,求![]() 和
和![]() 的值。
的值。
参考答案
一、1.A ;2.D;3.A;4.B;5.D;6.B;7.C;8.C;9.D;10.D;11.A;12.C
二、13. ![]() ;14.
;14.![]() ;15.
;15.![]() ;16.①②③.
;16.①②③.
三、17.![]() ;
;![]()
18.(1)![]() ;(2)略
;(2)略
19.(1) ![]() ;
;![]()
20.(1)![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]()
21.(1)1458辆;(2)2011
22.(1)略;(2)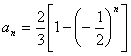 ;(3)
;(3)![]()