苏州十中2005-2006学年第一学期高一必修一模块考试试卷
数 学 (B)
2005.11.26
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设S={1,2,3},M={1,2},N={1,3},那么(![]() )∩(
)∩(![]() )等于
)等于
A. ![]() B.{1,3}
C.{1} D.{2,3}
B.{1,3}
C.{1} D.{2,3}
2. 对于函数![]() ,以下说法不正确的是
,以下说法不正确的是
A. ![]() 是
是![]() 的函数
B. 对于不同的
的函数
B. 对于不同的![]() 的值可以不同
的值可以不同
C. ![]() 表示当
表示当![]() 时函数
时函数![]() 的值 D.
的值 D. ![]() 一定可用一个具体的式子表示出来
一定可用一个具体的式子表示出来
3. 已知集合![]() ,
,![]() ,
,![]() 为集合
为集合![]() 到集合
到集合![]() 的一个函数,那么该函数的值域
的一个函数,那么该函数的值域![]() 的不同情况有( )种
的不同情况有( )种
A.6 B. 7 C. 8 D. 27
4. 已知![]() ,
,![]() ,则
,则![]() 用
用![]() 表示为
表示为
A.![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
5. 函数![]() 的图象必经过点
的图象必经过点
A. (0,1)
B. (1,1)
C. (2,0)
D. (2,2) ![]()
6. 已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() 表达式是
表达式是
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
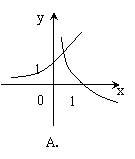
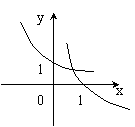
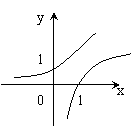
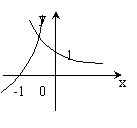
7. 函数![]() 与
与![]() 在同一坐标系中的图象只可能是
在同一坐标系中的图象只可能是
 |  |  | |||||
 | |||||||
|
|
|
8. 三个数![]() ,
,![]() ,
,![]() 的大小关系式是
的大小关系式是
A. ![]() <
<![]() <
<![]() B.
B. ![]() <
<![]() <
<![]() C.
C. ![]() <
<![]() <
<![]() D.
D. ![]() <
<![]() <
<![]()
9. 若![]()
A. 1 B. 3 C. 15 D. 30
10. 某人2003年1月1日到银行存入一年期存款a元,若按年利率为x,并按复利计算,到2008年1月1日可取回款
A. a(1+x)5元 B. a(1+x)6元 C. a(1+x5)元 D. a(1+x6)元
11. 如果函数![]() 在区间
在区间![]() 上递减,那么实数
上递减,那么实数![]() 的取值范围是
的取值范围是
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
12. 设![]() 是区间
是区间![]() 上的单调函数,且
上的单调函数,且![]() ,则方程
,则方程![]() 在区间
在区间![]()
A. 至少有一实根 B. 至多有一实根 C. 没有实根 D. 必有唯一实根
二、填空题(本大题6个小题,每小题3分,共18分,只填结果,不要过程)
13. 函数![]() 的值域是_________.
的值域是_________.
14. ![]() = _________.
= _________.
15. 已知![]() ,则
,则![]() _________.
_________.
16. 设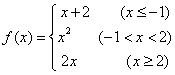 ,若
,若![]() ,则
,则![]() _________.
_________.
|
那么现在成本价格为8100元的计算机, 年后该计算机
的成本价格为1600元.
18. 如图所示的流程图是将一系列指令和问题用框图排列而成,
箭头将告诉你下一步到哪一个框图. 阅读右边的流程图,
并回答下面问题:若![]() ,则输出的数是
;
,则输出的数是
;
若![]() 则输出的数是 .
则输出的数是 .
(用字母a,b,c填空)
苏州十中2005-2006学年第一学期高一必修一模块考试试卷
数学答卷纸
2005.11.
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题(本大题6个小题,每小题3分,共18分,只填结果,不要过程)
13. 14.
15. 16.
17. 18.
.三、解答题:本大题6个小题,共46分.解答需写出必要的文字说明、推理过程或计算步骤
19. 设集合![]() ,若
,若![]() ,求实数
,求实数![]() 的值.
的值.
20. 已知函数![]() ,试作出函数的图象,并指出它的单调增区间,求出函数在
,试作出函数的图象,并指出它的单调增区间,求出函数在![]() 时的最大值.
时的最大值.
21. 已知函数![]() ,
,
(1)若![]() ,且函数
,且函数![]() 在区间(2,+∞)上是减函数,求
在区间(2,+∞)上是减函数,求![]() 的值;
的值;
(2)若![]() R, 且函数
R, 且函数![]() 恰有一根落在区间(-2,-1)内,求
恰有一根落在区间(-2,-1)内,求![]() 的取值范围.
的取值范围.
22. 设函数![]() 是定义在(0,+∞)上的减函数,并且满足
是定义在(0,+∞)上的减函数,并且满足![]() ,
,![]() .
.
(1)求![]() 的值;
的值;
(2)若存在实数m,使得![]() =2,求
=2,求![]() 的值;
的值;
(3)如果![]() ,求
,求![]() 的取值范围.
的取值范围.
23. 对于函数![]() ,若存在
,若存在![]() ,使
,使![]() 成立,则称点
成立,则称点![]() 为函数的不动点.
为函数的不动点.
(1)已知函数![]() 有不动点
有不动点![]() 和
和![]() ,求
,求![]() 、
、![]() 的值.
的值.
(2)若对于任意实数![]() ,函数
,函数![]() 总有两个相异的不动点,求实数
总有两个相异的不动点,求实数![]() 的取值范围.
的取值范围.
24. 设![]() 为奇函数,
为奇函数,![]() 为常数.
为常数.
(1) 求![]() 的值;
的值;
(2) 证明![]() 在区间(1,+∞)内单调递增;
在区间(1,+∞)内单调递增;
(3) 若对于区间[3,4]上的每一个![]() 的值,不等式
的值,不等式![]() >
>![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
苏州十中2005-2006学年第一学期高一必修一模块考试答案
数 学 (B)
一、选择题:本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的.
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | D | B | C | D | D | A | B | C | A | C | B |
二、填空题(本大题6个小题,每小题3分,共18分,只填结果,不要过程)
13. ![]() 14. 2 15. 2 16.
14. 2 15. 2 16. ![]() 17. 8 18.
17. 8 18.
![]() .
.
三、解答题:本大题6个小题,共46分.解答必需写出必要的文字说明、推理过程或计算步骤
19. 设集合![]() ,若
,若![]() ,求实数
,求实数![]() 的值.
的值.
解:由于,![]() ,且
,且![]() ,所以
,所以 
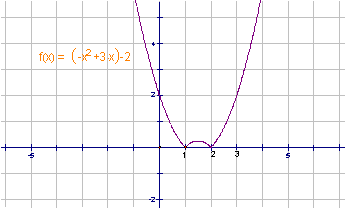
20.函数![]() 的单调增区间为〔1,1.5〕和〔2,∞〕;函数在
的单调增区间为〔1,1.5〕和〔2,∞〕;函数在![]() 时的最大值2.
时的最大值2.
21. 解:(1)![]() ,由于函数在(2,+∞)上递减,所以
,由于函数在(2,+∞)上递减,所以![]() 即
即![]() ,又
,又![]() ,所以
,所以![]() 或者
或者![]()
![]() 时,
时,![]() ;
;![]() 时,
时,![]()
(2)令![]()
![]()
![]()
![]()
当![]() 时,
时,
即![]() ,
,![]() 时函数可能有一根在所给区间中。
时函数可能有一根在所给区间中。
(或用根与系数的关系)
22. 解:(1)令![]() ,则
,则![]() ,∴
,∴![]()
(2)∵![]() ∴
∴![]()
∴m=2
(3)∴![]() ,
,
又由![]() 是定义在R+上的减函数,得:
是定义在R+上的减函数,得:
 解之得:
解之得: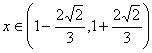 .
.
23. 解:(1)![]()
(2)由![]()
![]()
24.解:(1)∵ f(-x)=-f(x),∴![]() .
.
∴ ![]() ,即
,即![]() ,∴a=-1.
,∴a=-1.
(2)由(1)可知f(x)=![]()
![]() (x>1)
(x>1)
记u(x)=1+,由定义可证明u(x)在(1,+∞)上为减函数,
∴ f(x)=![]() 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
(3)设g(x)=![]() -
-![]() .则g(x)在[3,4]上为增函数.
.则g(x)在[3,4]上为增函数.
∴g(x)>m对x∈[3,4]恒成立,∴m<g(3)=-.