
2004-2005学年度上学期
高中学生学科素质训练
新课标高一数学同步测试(3)—第一单元(函数及其表示)
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确答案的代号填在题后的括号内(每小题5分,共50分).
1.下列四种说法正确的一个是 ( )
A.![]() 表示的是含有
表示的是含有![]() 的代数式 B.函数的值域也就是其定义中的数集B
的代数式 B.函数的值域也就是其定义中的数集B
C.函数是一种特殊的映射 D.映射是一种特殊的函数
2.已知f满足f(ab)=f(a)+
f(b),且f(2)=![]() ,
,![]() 那么
那么![]() 等于 ( )
等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列各组函数中,表示同一函数的是 ( )
A.![]() B.
B.![]()
C .![]() D.
D. ![]()
4.已知函数![]() 的定义域为 ( )
的定义域为 ( )
A.![]() B.
B.![]()
C .![]() D.
D. ![]()
5.设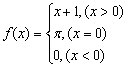 ,则
,则![]() ( )
( )
A.![]() B.0
C.
B.0
C.![]() D.
D.![]()
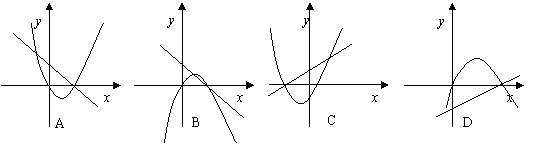
6.下列图中,画在同一坐标系中,函数![]() 与
与![]() 函数的图象只可能是 ( )
函数的图象只可能是 ( )
 |
7.设函数![]() ,则
,则![]() 的表达式为 ( )
的表达式为 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
8.已知二次函数![]() ,若
,若![]() ,则
,则![]() 的值为 ( )
的值为 ( )
A.正数 B.负数 C.0 D.符号与a有关
9.已知在![]() 克
克![]() 的盐水中,加入
的盐水中,加入![]() 克
克![]() 的盐水,浓度变为
的盐水,浓度变为![]() ,将y表示成x的函数关系式 ( )
,将y表示成x的函数关系式 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知![]() 的定义域为
的定义域为![]() ,则
,则![]() 的定义域为 ( )
的定义域为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:请把答案填在题中横线上(每小题6分,共24分).
11.已知![]() ,则
,则![]() =
.
=
.
12.若记号“*”表示的是![]() ,则用两边含有“*”和“+”的运算对于任意三个实数“a,b,c”成立一个恒等式
.
,则用两边含有“*”和“+”的运算对于任意三个实数“a,b,c”成立一个恒等式
.
13.集合A 中含有2个元素,集合A到集合A可构成 个不同的映射.
14.从盛满20升纯酒精的容器里倒出1升,然后用水加满,再倒出1升混合溶液,再用水加满. 这样继续下去,建立所倒次数![]() 和酒精残留量
和酒精残留量![]() 之间的函数关系式
.
之间的函数关系式
.
三、解答题:解答应写出文字说明、证明过程或演算步骤(共76分).
15.(12分)①.求函数![]() 的定义域;
的定义域;
②求函数![]() 的值域;
的值域;
③求函数![]() 的值域.
的值域.
16.(12分)在同一坐标系中绘制函数![]() ,
,![]() 得图象.
得图象.
17.(12分)已知函数![]() ,其中
,其中![]() ,求函数解析式.
,求函数解析式.
18.(12分)设![]() 是抛物线,并且当点
是抛物线,并且当点![]() 在抛物线图象上时,点
在抛物线图象上时,点![]() 在函数
在函数![]() 的图象上,求
的图象上,求![]() 的解析式.
的解析式.
19.(14分)动点P从边长为1的正方形ABCD的顶点出发顺次经过B、C、D再回到A;设![]() 表示P点的行程,
表示P点的行程,![]() 表示PA的长,求
表示PA的长,求![]() 关于
关于![]() 的函数解析式.
的函数解析式.
20.(14分)
已知函数![]() ,
,![]() 同时满足:
同时满足:![]() ;
;![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
参考答案(3)
一、CBCDA BCABC
二、11.-1; 12.![]() ; 13.4; 14.
; 13.4; 14.![]() ;
;
三、15. 解:①.因为![]() 的函数值一定大于0,且
的函数值一定大于0,且![]() 无论取什么数三次方根一定有意义,故其值域为R;
无论取什么数三次方根一定有意义,故其值域为R;
②.令![]() ,
,![]() ,
,![]() ,原式等于
,原式等于![]() ,故
,故![]() 。
。
③.把原式化为以![]() 为未知数的方程
为未知数的方程![]() ,
,
当![]() 时,
时,![]() ,得
,得![]() ;
;
当![]() 时,方程无解;所以函数的值域为
时,方程无解;所以函数的值域为![]() .
.
16.题示:对于第一个函数可以依据初中学习的知识借助顶点坐标,开口方向,与坐标轴交点坐标可得;第二个函数的图象,一种方法是将其化归成分段函数处理,另一种方法是该函数图象关于![]() 轴对称,先画好
轴对称,先画好![]() 轴右边的图象.
轴右边的图象.
17.题示:分别取![]() 和
和![]() ,可得
,可得
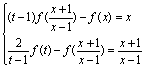 ,联立求解可得结果.
,联立求解可得结果.
18.解:令![]()
![]() ,也即
,也即![]() .同时
.同时
![]() =
=![]() =
=![]() .
.
通过比较对应系数相等,可得![]() ,也即
,也即![]() ,
,![]() 。
。
19.解:显然当P在AB上时,PA=![]() ;当P在BC上时,PA=
;当P在BC上时,PA=![]() ;当P在CD上时,
;当P在CD上时,
PA=![]() ;当P在DA上时,PA=
;当P在DA上时,PA=![]() ,再写成分段函数的形式.
,再写成分段函数的形式.
20.解:令![]() 得:
得:![]() . 再令
. 再令![]() ,即得
,即得![]() . 若
. 若![]() ,令
,令![]() 时,得
时,得![]() 不合题意,故
不合题意,故![]() ;
;![]() ,即
,即![]() ,所以
,所以![]() ;那么
;那么![]() ,
,![]() .
.