高一期未课本基础知识回顾
广州市第八十六中学 贾国富
一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确的答案填在答题卡中.
(1)若![]() 则使
则使![]() 和
和![]() 同时成立的
同时成立的![]() 的取值范围是 ( )
的取值范围是 ( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
![]()
![]()
(2)把函数![]() 的图象向左平移
的图象向左平移![]() 个单位,所得的图象
个单位,所得的图象![]() 轴对称,则
轴对称,则
![]() 的最小正值是
( )
的最小正值是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(3)要得到![]() 的图象,只需将
的图象,只需将![]() 的图象 ( )
的图象 ( )
(A)向左平移![]() 个单位 (B)向右平移
个单位 (B)向右平移![]() 个单位
个单位
(C) 向左平移![]() 个单位
(D)向右平移
个单位
(D)向右平移![]() 个单位
个单位
(4)已知![]() 点
点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() 则点
则点![]() 分
分![]() 所成的比是( )
所成的比是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)
![]()
(5)若命题:![]()
![]() 命题
命题![]() 则命题
则命题![]() 是命题
是命题![]() 的
( )
的
( )
(A)充分不必要条件(B)必要不充分条件(C)充要条件(D)即不必要也不充分条件
(6)下列命题是假命题的是 ( )
(A)对于两个非零向量![]() ,若存在一个实数
,若存在一个实数![]() 满足
满足![]() 则
则![]() 共线
共线
(B) 若![]() ,则
,则![]()
(C)若![]() 为两个非零向量,则
为两个非零向量,则![]()
(D) 若![]() 为两个方向相同的向量,则
为两个方向相同的向量,则![]()
(7)已知向量![]() 如果
如果![]() 与
与![]() 垂直,则
垂直,则![]() 的值为
( )
的值为
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(8)△ABC满足下列条件之一:①![]() ②
②![]()
③![]() ④
④![]()
其中有两个解的是 ( )
(A)①② (B)①④ (C)①②③ (D)③④
(9)设![]() 且
且![]() 则下列结论正确的是
( )
则下列结论正确的是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
(10)已知函数![]() 构造函数
构造函数![]() 定义如下:当
定义如下:当![]()
时,![]() 当
当![]() 时,
时,![]() 那么
那么![]() ( )
( )
(A) 有最小值![]() ,无最大值
(B)有最小值
,无最大值
(B)有最小值![]() ,无最大值
,无最大值
(C)有最大值![]() ,无最小值 (D)无最小值,也无最大值
,无最小值 (D)无最小值,也无最大值
(11)不等式组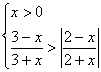 的解集是
( )
的解集是
( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
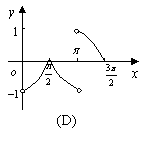
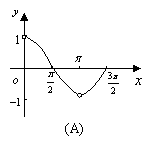
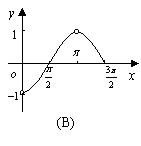
 (12)函数
(12)函数![]() 且
且![]() 的图象是
( )
的图象是
( )
请把选择题的答案填在下面的表格内:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、 填空题(每小题4分,共16分)
(13) 函数![]() 的定义域为 .
的定义域为 .
(14) 函数![]() 的图象按向量
的图象按向量![]() 平移后,图象的解析式为
平移后,图象的解析式为![]() ,则向量
,则向量![]()
![]() .
.
(15) 函数![]() 的单调增区间是
.
的单调增区间是
.
(16)给出下列命题:①存在实数![]() 使
使![]() ②存在实数
②存在实数![]() 使
使![]() ③
③![]() 是偶函数④
是偶函数④![]() 是
是![]() 的一条对称方程⑤若
的一条对称方程⑤若![]() 是第一象限角,则
是第一象限角,则![]() .其中正确命题的序号是
.(注:把你认为正确命题的序号都填上)
.其中正确命题的序号是
.(注:把你认为正确命题的序号都填上)
三、解答题(请写出详细的推演过程)
(17)(本小题满分12分)
已知函数![]()
①求![]() 的定义域;
的定义域;
②用定义判断![]() 的奇偶性;
的奇偶性;
③在![]() 上作出函数
上作出函数 ![]() 的图象;
的图象;
④指出![]() 的最小正周期及单调递增区间.
的最小正周期及单调递增区间.
(18)(本小题满分12分)
解关于![]() 的不等式:
的不等式:![]()
 (19)(本小题满分12分)
(19)(本小题满分12分)
如图为余弦函数![]() 在一个周期内的图象.
在一个周期内的图象.
①写出![]() 的解析式;
的解析式;
②若![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,写出
对称,写出![]() 的解析式;
的解析式;
③求![]() 的单调区间.
的单调区间.
(20)(本小题满分12分)
设两个非零向量![]() 不共线.
不共线.
(1)如果![]()
![]()
![]()
![]()
![]()
![]()
求证:![]() 三点共线;
三点共线;
(2)试确定实数![]() 使
使![]()
![]() 共线;
共线;
(3)若![]()
![]() 夹角为
夹角为![]() ,试确定
,试确定![]() ,使
,使![]()
![]() 垂直.
垂直.
(21)(本小题满分12分)
若![]() 且
且![]() 求证:
求证:![]()
(22)(本小题满分14分)
如图所示,某校把一块边长为![]() 的等边
的等边![]() 的边角辟为生物园,图中
的边角辟为生物园,图中![]() 把生物园分成面
把生物园分成面
积相等的两部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.
(1)设![]() 求用
求用![]() 表示
表示![]() 的函数关系式.
的函数关系式.
(2)
|
|
|
| ||||
| ||||
