金乡高级中学第三次月考高一数学试题
一、选择题(本大题共10小题,每小题5分,满分50分)
1、已知全集![]() ,集合
,集合![]() ,
,![]() ,则集合
,则集合![]() (
(![]() U
U![]() )等于( )
)等于( )
![]()
![]() 或
或![]()
![]()
![]() 或
或![]()
![]()
![]() 或
或![]()
![]()
![]() 或
或![]()
2、若函数![]() 的反函数的图象过
的反函数的图象过![]() 点,则
点,则![]() 点坐标可能是 ( )
点坐标可能是 ( )
A、(2,5) B、(1,3) C、(5,2) D、(3,1)
3、已知![]() 是第三象限角,
是第三象限角,![]() 且
且![]() ,则
,则![]() 等于 ( )
等于 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、已4知sin![]() cos
cos![]() =
=![]() ,且
,且![]()
![]()
![]() ,则cos
,则cos![]() -sin
-sin![]() 的值为( )
的值为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5、若数列![]() 的前
的前![]() 项之和
项之和![]() ,那么这个数列的通项公式为( )
,那么这个数列的通项公式为( )
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6、不等式![]() 的解集是 ( )
的解集是 ( )
A、![]() B、[-1,3] C、
B、[-1,3] C、![]() D、
D、![]()
7、已知数列![]() 中,
中,![]() ,则
,则![]() 等于( )
等于( )
![]() 445
445 ![]() 765
765 ![]() 1080
1080
![]() 3105
3105
8、将函数y=f(x)sinx的图象向右平移![]() 个单位后,再作关于x轴对称的曲线,得到函数y=1-2sin2x,
则f(x)是
( )
个单位后,再作关于x轴对称的曲线,得到函数y=1-2sin2x,
则f(x)是
( )
A.cosx B.2cosx C.sinx D.2sinx
9、若![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为 ( )
的夹角为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
10、已知函数![]() 为偶函数,其图象与直线
为偶函数,其图象与直线![]() 的某两个交点横坐标为
的某两个交点横坐标为![]() ,
,![]() 的最小值为
的最小值为![]() ,则 ( )
,则 ( )
A、![]() ,
,![]() B、
B、![]() ,
,![]() C、
C、![]() ,
,![]() D、
D、![]() ,
,![]()
二、填空题(本大题共4小题,每小题4分,满分16分)
11、若![]() ,
,![]() ,则
,则![]() =__________。
=__________。
12、已知![]() ,
,![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,要使
,要使![]()
![]()
![]() 与
与![]() 垂直,则
垂直,则![]() =
。
=
。
13、在“ + ![]() ”中的“
”处分别填上一个自然数,并使它们的和最小;
”中的“
”处分别填上一个自然数,并使它们的和最小;
14、定义运算![]() 为:
为:![]() 例如,
例如,![]() ,则函数f(x)=
,则函数f(x)=![]() 的值域为 .
的值域为 .
金乡高级中学第三次月考答题纸
一、选择题(本大题共10小题,每小题5分,满分50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题(本大题共4小题,每小题4分,满分16分)
11、 12、 13、 14、
三、解答题(本大题共6小题,满分84分)
15、(本题满分14分)已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,
,
⑴求函数![]() ;⑵解不等式
;⑵解不等式![]() 。
。
16、(本题满分14分)已知函数![]() 、
、![]() 为 常数,且
为 常数,且![]() )的图象过点(0,
)的图象过点(0,![]() ),且函数
),且函数![]() 的最大值为2。
的最大值为2。
⑴求函数![]() 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
⑵若函数![]() 的图象按向量
的图象按向量![]() 作移动距离最小的平移后,使所得图象关于
作移动距离最小的平移后,使所得图象关于![]() 轴对称,求出向量
轴对称,求出向量![]() 的坐标及平移后的图象对应的函数解析式。
的坐标及平移后的图象对应的函数解析式。
17、(本题满分14分)设![]() 、
、![]() 是两个不共线的非零向量(
是两个不共线的非零向量(![]() )
)
⑴设![]() ,
,![]() ,
,![]() 那么当实数
那么当实数![]() 为何值时,
为何值时,![]() 、
、![]() 、
、![]() 三点共线?
三点共线?
⑵若![]()
![]() 且
且![]() 与
与![]() 夹角为120°,那么实数
夹角为120°,那么实数![]() 为何值时
为何值时![]() 的值最小?
的值最小?
18、(本题满分14分)某造纸厂拟建一座平面图形为矩形且面积为200平方米的二级污水处理池(平面图如图所示),池的深度一定,池的外圈周壁建造单价为每米400元,中间一条隔壁建造单价为每米100元,池底建造单价每平方米60元(池壁厚忽略不计)
⑴污水处理池的长设计为多少米时,可使总造价最低;
⑵如果受地形限制,污水处理池的长、宽都不能超过14.5米,那么此时污水处理池的长设计为多少米时,可使总造价最低。
19、(本小题满分14分)已知函数![]()
![]() 、
、![]() 为常数,且
为常数,且![]() ,若
,若![]() ,且方程
,且方程![]() 有两个相等的实根。(1)求函数
有两个相等的实根。(1)求函数![]() 的表达式;(2)设数列
的表达式;(2)设数列![]() 满足条件:
满足条件:![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式。
的通项公式。
20.(本题满分14分) 已知数列{an}中,a1>0, 且an+1=![]() ,
,
(Ⅰ)试求a1的值,使得数列{an}是一个常数数列;
(Ⅱ)试求a1的取值范围,使得an+1>an对任何自然数n都成立;
(Ⅲ)若a1 = 2,设bn = an+1-an (n = 1,2,3,…),并以Sn表示数列{bn}的前n项的和,求证:Sn<![]() .
.
金乡高级中学第三次月考答题纸
四、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | C | D | B | D | C | B | B | C | A |
五、填空题
11、-![]() 12、2 13、10 15 14、[-1,
12、2 13、10 15 14、[-1,![]() ]
]
六、解答题
15、(本题满分14分)已知![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,![]() ,
,
⑴求函数![]() ;⑵解不等式
;⑵解不等式![]() 。
。
f(x)=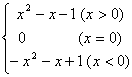 x=0显然成立
x=0显然成立 ![]() 得 0<x<2
得 0<x<2 ![]()
![]() 得 x<-1 综述(-
得 x<-1 综述(-![]() -1)
-1)![]()
![]()
16、(本题满分14分)已知函数![]() 、
、![]() 为 常数,且
为 常数,且![]() )的图象过点(0,
)的图象过点(0,![]() ),且函数
),且函数![]() 的最大值为2。
的最大值为2。
⑴求函数![]() 的解析式,并写出其单调递增区间;
的解析式,并写出其单调递增区间;
⑵若函数![]() 的图象按向量
的图象按向量![]() 作移动距离最小的平移后,使所得图象关于
作移动距离最小的平移后,使所得图象关于![]() 轴对称,求出向量
轴对称,求出向量![]() 的坐标及平移后的图象对应的函数解析式。
的坐标及平移后的图象对应的函数解析式。
解:(1)![]()
![]()
所以函数![]() 的解析式是
的解析式是![]()
![]() 的单调递增区间是
的单调递增区间是![]()
(2)∵平移后的图象对应的函数解析式是![]()
图象关于y轴对称,即![]() 为偶函数,
为偶函数,
![]()
![]() 恒成立
恒成立
![]()
![]() ,
, ![]()
故![]()
![]() ,图象对应的函数解析式为
,图象对应的函数解析式为![]()
17、(本题满分14分)设![]() 、
、![]() 是两个不共线的非零向量(
是两个不共线的非零向量(![]() )
)
⑴设![]() ,
,![]() ,
,![]() 那么当实数
那么当实数![]() 为何值时,
为何值时,![]() 、
、![]() 、
、![]() 三点共线?
三点共线?
⑵若![]()
![]() 且
且![]() 与
与![]() 夹角为120°,那么实数
夹角为120°,那么实数![]() 为何值时
为何值时![]() 的值最小?
的值最小?
(1)
![]() ,
,![]()
![]()
![]()
(2)![]()
![]()
![]()
18、(本题满分14分)某造纸厂拟建一座平面图形为矩形且面积为200平方米的二级污水处理池(平面图如图所示),池的深度一定,池的外圈周壁建造单价为每米400元,中间一条隔壁建造单价为每米100元,池底建造单价每平方米60元(池壁厚忽略不计)
⑴污水处理池的长设计为多少米时,可使总造价最低;
⑵如果受地形限制,污水处理池的长、宽都不能超过14.5米,那么此时污水处理池的长设计为多少米时,可使总造价最低。
解:设污水处理池的长为x米,则宽为![]() 米。
米。
总造价![]() 。
。
![]()
![]()
=36000(元)
当且仅当![]() 时,即x=15等号成立。
时,即x=15等号成立。
记g(x)=x+![]() ,显然是减函数,
,显然是减函数,
![]() 有最小值,相应造价f(x)有最小值。此时宽也不超过14.5
有最小值,相应造价f(x)有最小值。此时宽也不超过14.5
19、(本小题满分14分)已知函数![]()
![]() 、
、![]() 为常数,且
为常数,且![]() ,若
,若![]() ,且方程
,且方程![]() 有两个相等的实根。(1)求函数
有两个相等的实根。(1)求函数![]() 的表达式;(2)设数列
的表达式;(2)设数列![]() 满足条件:
满足条件:![]() ,且
,且![]() ,求数列
,求数列![]() 的通项公式。
的通项公式。
解 :(1)∵f(2)=1,∴![]() ① 又f(x)=x,即
① 又f(x)=x,即![]() ,化简得ax2+(b—1)x=0(a≠0),
,化简得ax2+(b—1)x=0(a≠0),
又因为方程f(x)=x有两个相等的实根,∴△=(b—1)2=0,
解得b=1,把它带入①式解得a=![]() ,∴ f(x)=
,∴ f(x)=![]()
(2)∵由(1)知f(x)=
![]() ,则
,则![]()
由Xn+1=f(Xn),X1=2,则![]()
![]() ,
,![]()
所以![]() 故数列{
故数列{![]() }是以
}是以![]() 为首项,以
为首项,以![]() 为公差的等差数列
为公差的等差数列
∴![]() =
=![]() +(n—1)
+(n—1)![]() =
=![]() ,∴数列
,∴数列![]() 的通项公式为
的通项公式为![]() 。
。
20.(本题满分14分) 已知数列{an}中,a1>0, 且an+1=![]() ,
,
(Ⅰ)试求a1的值,使得数列{an}是一个常数数列;
(Ⅱ)试求a1的取值范围,使得an+1>an对任何自然数n都成立;
(Ⅲ)若a1 = 2,设bn = an+1-an (n = 1,2,3,…),并以Sn表示数列{bn}的前n项的和,求证:Sn<![]() .
.
解:(Ⅰ)欲使数列{an}是一个常数数列,则an+1=![]() = an ……………………
= an ……………………
又依a1>0,可得an>0并解出:an=![]() ,即a1 = an =
,即a1 = an =![]() ……………………
……………………
(Ⅱ)研究an+1-an=![]() -
-![]() =
=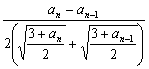 (n≥2)
(n≥2)
注意到![]() >0
>0
因此,可以得出:an+1-an,an-an-1,an-1-an-2,…,a2-a1有相同的符号
要使an+1>an对任意自然数都成立,只须a2-a1>0即可.
由![]() >0,解得:0<a1<
>0,解得:0<a1<![]() ……………………………………………
……………………………………………
(Ⅲ)用与(Ⅱ)中相同的方法,可得
当a1>![]() 时,an+1<an对任何自然数n都成立.
时,an+1<an对任何自然数n都成立.
因此当a1=2时,an+1-an<0 ……………………………………………
∴ Sn= b1+b2+…bn
=a2-a1 + a3-a2 +…+ an+1-an
=a1-a2+a2-a3+…+an-an+1
=a1-an+1=2-an+1 ………………………………………………………
又:an+2=![]() < an+1,可解得an+1>
< an+1,可解得an+1>![]() ,
,
故Sn<2-![]() =
=![]() ………………………………………………………………
………………………………………………………………