高二数学下学期期末模拟试题
本试卷满分150分,答题时间 120分钟
姓名 班级 分数
一.选择题:(每小题5分,共50分)
1.设a、b、c是三个实数,那么“a>b”是“![]() ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.设向量![]() 不共面,则下列集合可作为空间的一个基底的是( )
不共面,则下列集合可作为空间的一个基底的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.将一个骰子连续抛掷三次,它落地时向上的点数依次成等差数列的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.当x∈![]() 时,可得到不 等
式x+
时,可得到不 等
式x+![]()
![]() 2,x+
2,x+![]()
![]() 3,由
此可推广为x+
3,由
此可推广为x+![]()
![]() n+1,其中P等于( )
n+1,其中P等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知两定点![]() ,如果动点
,如果动点![]() 满足
满足![]() ,则点
,则点![]() 的轨迹所包围的图形的面积等于( )
的轨迹所包围的图形的面积等于( )
| 3 | ||
| 4 | ||
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.将1,2,3,…,9这9个数字填在如图中的9个空格中,要求每一行从左到右,每一列从上到下依次增大.当3,4固定在图中位置时,填写空格的方法种数是( )
A.6
B.
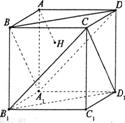 7.如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,错误的命题是( )
7.如图,正方体AC1的棱长为1,过点A作平面A1BD的垂线,垂足为点H.则以下命题中,错误的命题是( )
A.点H是△A1BD的垂心
B.AH垂直平面CB1D1
C.AH的延长线经过点C1
D.直线AH和BB1所成角为45°
8.已知集合![]() ,直线
,直线![]() 与双曲线
与双曲线![]() 有且只有一个公共点,其中
有且只有一个公共点,其中![]() ,则满足上述条件的双曲线共有( )
,则满足上述条件的双曲线共有( )
A.2条 B.3条 C.4条 D.以上答案都不对
9.如果![]() ∥
∥![]() ,AB与AC是夹在平面
,AB与AC是夹在平面![]() 与
与![]() 之间的两条线段,
之间的两条线段,![]() 且
且![]() ,直线AB与平面
,直线AB与平面![]() 所成的角为
所成的角为![]() ,那么线段AC长的取值范围是( )
,那么线段AC长的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.设椭圆![]() 的离心率为e=
的离心率为e=![]() ,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P (x1,x2) 的位置( )
,右焦点为F(c,0),方程ax2+bx-c=0的两个实根分别为x1和x2,则点P (x1,x2) 的位置( )
A.必在圆x2+y2=2内 B.必在圆x2+y2=2上
C.必在圆x2+y2=2外 D.以上三种情形都有可能
答 题 卡
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
二.填空题:(每小题5分,共25分)
11.用一张长宽分别为
为___ _ cm
12.已知点P(x, y)的坐标满足条件 ,点O为坐标原点,那么PO的最小值等于_________,最大值等于____________。
,点O为坐标原点,那么PO的最小值等于_________,最大值等于____________。
13.过抛物线![]() 的焦点
的焦点![]() 作倾角为
作倾角为![]() 的直线,与抛物线分别交于
的直线,与抛物线分别交于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 轴左侧),则
轴左侧),则![]() 。
。
14.一个类似于杨辉三角的三角形数组(如下图)满足:(1)第1行只有1个数1;
(2)当n≥2时,第n行首尾两数均为n; (3)当n>2时,中间各数都等于它肩上两数之和,则第n行(n≥2)第2个数是______________ _。
1
2 2
3 4 3
4 7 7 4
…………………………………………………………
15.已知O为异面直线a、b外任一点,给出下列命题:
①过点O可以作一条直线与a、b都相交; ②过点O可以作一个平面与a、b都平行;③过点O可以作一条直线与a、b都垂直; ④过点O可以作一个平面与a、b都垂直。
其中真命题的编号是 (写出所有正确命题的编号)。
三.解答题:
16.(本小题满分12分)已知函数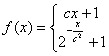
![]() ,且
,且![]() .
.
(1)求常数![]() 的值;(2)解不等式
的值;(2)解不等式![]() 。
。
17.(本小题满分12分)在1,2,3,,…,30,这30个数中。(1)每次取互不相等的2个数,使其积为7的倍数,有多少种取法?(2)每次取互不相等的3个数,使其和是4的倍数,有多少种取法?
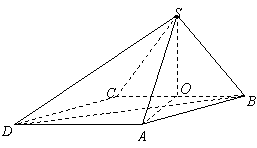
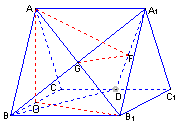
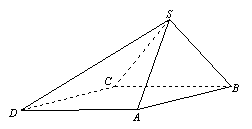 18.(本小题满分12分)四棱锥
18.(本小题满分12分)四棱锥![]() 中,底面
中,底面![]() 为平行四边形,侧面
为平行四边形,侧面![]() 底面
底面![]() .已知
.已知![]() ,
,![]() ,
,![]() ,
,![]() .(Ⅰ)证明
.(Ⅰ)证明![]() ;(Ⅱ)求直线
;(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的大小.
所成角的大小.

19.(本小题满分12分)如图,设ABCDEF为正六边形,一只青蛙从顶点A开始随机跳动,每次随机地跳到与它所在顶点相邻的两顶点之一,每次按顺时针方向跳动的概率为![]() .
.
(1)求青蛙从A点开始经过3次跳动所处的位置为D点概率;
(2)求青蛙从A点开始经过4次跳动所处的位置为E点概率.
 20.(本小题满分13分)如图,正三棱柱
20.(本小题满分13分)如图,正三棱柱![]() 的所有棱长都为
的所有棱长都为![]() ,
,![]() 为
为![]() 中点
中点![]() (Ⅰ)求证:
(Ⅰ)求证:![]() 平面
平面![]() ;(Ⅱ)求二面角
;(Ⅱ)求二面角![]() 的大小;(Ⅲ)求点
的大小;(Ⅲ)求点![]() 到平面
到平面![]() 的距离
的距离![]()
21.(本小题满分14分)已知椭圆![]() 的离心率为
的离心率为![]() ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为![]() .(Ⅰ)求椭圆
.(Ⅰ)求椭圆![]() 的方程;(Ⅱ)设直线
的方程;(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,坐标原点
两点,坐标原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 面积的最大值.
面积的最大值.
湖北省安陆一中高二下学期期末模拟试题参考答案
一.选择题:(每小题5分,共50分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | C | B | A | B | A | D | C | D | A |
二.填空题:(每小题5分,共25分)
11.![]() 12.
12.![]() 13.
13.![]() 14.
14.![]() 15.③
15.③
三.解答题:
16.解:(1)因为![]() 所以
所以![]() 又由于
又由于![]() 。所以
。所以![]() 可得
可得![]()
(2)由(1)知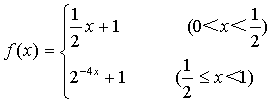
当![]() 时,
时,![]() ,因为
,因为![]() ,所以
,所以![]()
当![]() 时,
时,![]() ,所以
,所以![]()
综上得不等式的解集为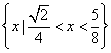
17.解:(1)被7整除的数有7,14,21,28四个,不被7整除的有26个,满足题意的取法共有![]() =6+104=110
=6+104=110
(2)记![]() 表示被4除余
表示被4除余![]() 的数组成的集合(
的数组成的集合(![]() =0,1,2,3)
=0,1,2,3)
![]() 共有7个元素,
共有7个元素, ![]() 共有8个元素
共有8个元素
![]() 共有8个元素,
共有8个元素,![]() 共有7个元素
共有7个元素
满足题意的取法:1、在![]() 中取3个,有
中取3个,有![]() =35种。
=35种。
2、在![]() 中取1个、
中取1个、![]() 中取2个,有
中取2个,有![]() =196种。
=196种。
3、在![]() 中取1个、
中取1个、![]() 和
和![]() 中各取1个,有
中各取1个,有![]() =392种。
=392种。
4、在![]() 中取2个、
中取2个、![]() 中取1个,有
中取1个,有![]() =224种
=224种
5、在![]() 中取1个、
中取1个、![]() 中取2个,有
中取2个,有![]() =168种。故共有1015种取法。
=168种。故共有1015种取法。
18.解:(Ⅰ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 底面
底面![]() .因为
.因为![]() ,所以
,所以![]() ,又
,又![]() ,故
,故![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,由三垂线定理,得
,由三垂线定理,得![]() .
.
(Ⅱ)由(Ⅰ)知![]() ,依题设
,依题设![]() ,
,
故![]() ,由
,由![]() ,
,![]() ,
,![]() ,得
,得![]() ,
,![]() .
.
![]() 的面积
的面积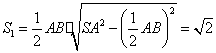 .连结
.连结![]() ,得
,得![]() 的面积
的面积![]()
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由于
,由于![]() ,得
,得
![]() ,解得
,解得![]() .
.
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,则
,则
![]() .所以,直线
.所以,直线![]() 与平面
与平面![]() 所成的我为
所成的我为![]() .
.
解法二:(Ⅰ)作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() ,由侧面
,由侧面![]() 底面
底面![]() ,得
,得![]() 平面
平面![]() .因为
.因为![]() ,所以
,所以![]() .又
.又![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.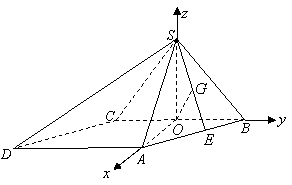 如图,以
如图,以![]() 为坐标原点,
为坐标原点,![]() 为
为![]() 轴正向,建立直角坐标系
轴正向,建立直角坐标系![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
(Ⅱ)取![]() 中点
中点![]() ,
,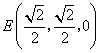 ,连结
,连结![]() ,取
,取![]() 中点
中点![]() ,连结
,连结![]() ,
,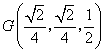 .
.
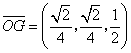 ,
,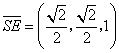 ,
,![]() .
.![]() ,
,![]() ,
,![]() 与平面
与平面![]() 内两条相交直线
内两条相交直线![]() ,
,![]() 垂直.所以
垂直.所以![]() 平面
平面![]() ,
,![]() 与
与![]() 的夹角记为
的夹角记为![]() ,
,![]() 与平面
与平面![]() 所成的角记为
所成的角记为![]() ,则
,则![]() 与
与![]() 互余.
互余.![]() ,
,![]() .
.
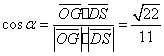 ,
,![]() ,
,
所以,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
19.解:设青蛙顺时针跳动1次为事件A,逆时针跳动1次为事件B,则, P(A)=![]() ,P(B)=1-P(A)=
,P(B)=1-P(A)=![]() 。
。
青蛙从A点开始经过3次跳动到达D点有两种方式:顺时针跳动3次或逆时针跳动3次,故所求概率为P(A·A·A)+P(B·B·B)=![]()
(2)青蛙从A点开始经过4次跳动到达E点有两种方式:逆时针跳动4次,或顺时针跳动3次而逆时针跳动1次,逆时针跳动4次的概率为![]() ,顺时针跳动3次而逆时针跳动1次的概率为
,顺时针跳动3次而逆时针跳动1次的概率为![]() 。故所求概率为
。故所求概率为![]() .
.
 20.解法一:(Ⅰ)取
20.解法一:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]()
![]()
![]() 为正三角形,
为正三角形,![]()
![]()
![]() 正三棱柱
正三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,
![]() 平面
平面![]()
![]() 连结
连结![]() ,在正方形
,在正方形![]() 中,
中,![]() 分别为
分别为![]() 的中点,
的中点,![]() ,
,![]()
![]()
在正方形![]() 中,
中,![]() ,
,![]() 平面
平面![]()
![]()
(Ⅱ)设![]() 与
与![]() 交于点
交于点![]() ,在平面
,在平面![]() 中,作
中,作![]() 于
于![]() ,连结
,连结![]() ,由(Ⅰ)得
,由(Ⅰ)得![]() 平面
平面![]()
![]()
![]() ,
,![]() 为二面角
为二面角![]() 的平面角
的平面角![]()
在![]() 中,由等面积法可求得
中,由等面积法可求得![]() ,又
,又![]() ,
,
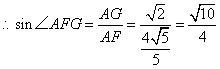
![]() 所以二面角
所以二面角![]() 的大小为
的大小为![]()
![]()
(Ⅲ)![]() 中,
中,![]() ,
,![]()
![]() 在正三棱柱中,
在正三棱柱中,![]() 到平面
到平面![]() 的距离为
的距离为![]()
![]() 设点
设点![]() 到平面
到平面![]() 的距离为
的距离为![]()
![]()
 由
由![]() 得
得![]() ,
,
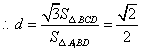
![]()
![]() 点
点![]() 到平面
到平面![]() 的距离为
的距离为![]()
![]()
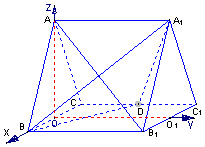
解法二:(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]()
![]()
![]() 为正三角形,
为正三角形,![]()
![]()
![]() 在正三棱柱
在正三棱柱![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 取
取![]() 中点
中点![]() ,以
,以![]() 为原点,
为原点,![]() ,
,![]() ,
,![]() 的方向为
的方向为![]() 轴的正方向建立空间直角坐标系,则
轴的正方向建立空间直角坐标系,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() 平面
平面![]()
![]()
(Ⅱ)设平面![]() 的法向量为
的法向量为![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,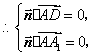
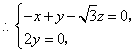
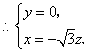
令![]() 得
得![]() 为平面
为平面![]() 的一个法向量
的一个法向量![]() 由(Ⅰ)知
由(Ⅰ)知![]() 平面
平面![]() ,
,
![]() 为平面
为平面![]() 的法向量
的法向量![]()
![]() ,
,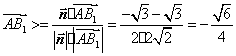
![]()
![]() 二面角
二面角![]() 的大小为
的大小为![]()
![]()
(Ⅲ)由(Ⅱ),![]() 为平面
为平面![]() 法向量,
法向量, ![]()
![]()
![]() 点
点![]() 到平面
到平面![]() 的距离
的距离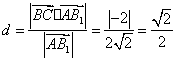
21.解:(Ⅰ)设椭圆的半焦距为![]() ,依题意
,依题意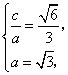 ,
,![]() ,
,![]() 所求椭圆方程为
所求椭圆方程为![]() .
.
(Ⅱ)设![]() ,
,![]() .(1)当
.(1)当![]() 轴时,
轴时,![]() .
.
(2)当![]() 与
与![]() 轴不垂直时,设直线
轴不垂直时,设直线![]() 的方程为
的方程为![]() .
.
由已知![]() ,得
,得![]() .把
.把![]() 代入椭圆方程,整理得
代入椭圆方程,整理得![]() ,
,![]() ,
,![]() .
.
![]()

![]()
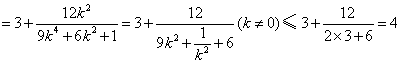 .
.
当且仅当![]() ,即
,即![]() 时等号成立.当
时等号成立.当![]() 时,
时,![]() ,
,
综上所述![]() .
.![]() 当
当![]() 最大时,
最大时,![]() 面积取最大值
面积取最大值![]() .
.