高二数学下期末考试综合练习(1)
高二 班 学号 姓名 成绩
一、填空题
1、![]()
![]() 。
。
2、若![]() ,
,![]() ,则
,则![]() 与
与![]() 的位置关系为
的位置关系为![]() 。
。
3、设正三棱椎![]() 的底边长为
的底边长为![]() ,高为
,高为![]() ,则侧棱与底面所成角的大小为
,则侧棱与底面所成角的大小为![]() 。
。
4、在等比数列![]() 中,公比为
中,公比为![]() 且
且![]() ,若
,若![]() ,
,![]() ,则
,则![]()
![]() 。
。
解:![]() ,
,![]() ,
,![]()
![]() 。
。
因为![]() ,解得
,解得![]() ,
,![]() ,所以
,所以![]() 。
。
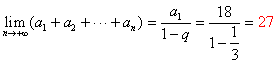 。
。
5、已知![]() ,
,![]() ,
,![]() ,则当
,则当![]() 最大时
最大时![]() 与
与![]() 的夹角
的夹角![]()
![]() 。
。
解:![]()
![]() ,当
,当![]() 时,
时,![]() 最大。
最大。
此时![]() ,代入得
,代入得![]() ,
,![]() 。
。
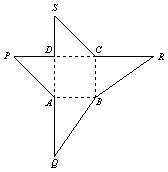 因为
因为![]() ,所以
,所以![]() 与
与![]() 的夹角
的夹角![]()
![]() 。
。
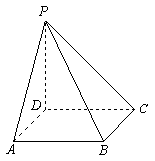
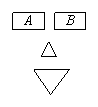
6、如图为一几何体的展开图,其中![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() ,
,![]() ,
,![]() ,点
,点![]() 及
及![]() 共线,沿图中虚线将它们折叠起来,使
共线,沿图中虚线将它们折叠起来,使![]() 四点重合,则需要
四点重合,则需要![]() 个这样的几何体,可以拼成一个棱长为
个这样的几何体,可以拼成一个棱长为![]() 的正方体。
的正方体。
解: 折叠后的样子 三个四棱锥的拼法
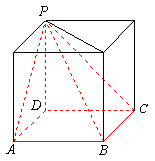
 7、 用
7、 用![]() 种不同的颜色给图中的“笑脸”涂色,要求“眼睛”(即图中
种不同的颜色给图中的“笑脸”涂色,要求“眼睛”(即图中![]() 所示区域)用相同颜色,则不同的涂法共有
所示区域)用相同颜色,则不同的涂法共有![]() 种。(用数字作答)
种。(用数字作答)
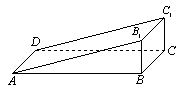 8、 如图,直三棱柱
8、 如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 上有一动点
上有一动点![]() ,则
,则![]() 周长的最小值是
周长的最小值是![]() 。
。
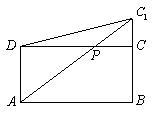 解:
解:![]() ,
,
要使![]() 最小,须将图展开,连接
最小,须将图展开,连接![]() 交
交![]() 于
于![]() ,此时
,此时![]() 。
。
所以![]() 周长的最小值是
周长的最小值是![]() 。
。
9、 ![]() 件产品,其中
件产品,其中![]() 件是正品,
件是正品,![]() 件是次品,从中任抽
件是次品,从中任抽![]() 两件最多
两件最多![]() 件是次品的概率等于
件是次品的概率等于![]() 。
。
10、若在从![]() 到
到![]() 这
这![]() 个整数中任取
个整数中任取![]() 个数 ,则所取的两数和为偶数的概率为
个数 ,则所取的两数和为偶数的概率为![]() 。
。
11、已知数列![]() 是由正整数组成的数列,
是由正整数组成的数列,![]() ,且满足
,且满足![]() ,其中
,其中![]() ,
,![]() ,且
,且![]() ,则
,则![]()
![]() 。
。
解:当![]() 时,
时,![]()
![]() ,
,![]() (
(![]() )。
)。
所以![]() 。
。
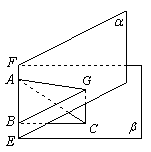 12、在锐角的二面角
12、在锐角的二面角![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() 与
与![]() 所成角为
所成角为![]() ,则二面角
,则二面角![]() 为
为![]() 。
。
解:如图,作![]() ,交
,交![]() 于
于![]() 。过
。过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() 。
。
设![]() ,则
,则![]() ,
,![]() 。
。
因为![]() ,所以
,所以![]() ,则
,则![]() 。
。
二、选择题
13、从单词“![]() ”选取
”选取![]() 个不同的字母排成一排,含有“
个不同的字母排成一排,含有“![]() ”(其中“
”(其中“![]() ”相连且顺序不变)的不同排列共有个数为(
”相连且顺序不变)的不同排列共有个数为(![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
解:![]() 。
。
14、探索以下的规律: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
则根据规律,从![]() 到
到![]() ,箭头的方向依次为(
,箭头的方向依次为(![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
解:以4为周期,故从![]() 到
到![]() 相当于从2到4。
相当于从2到4。
15、若![]() 是直三棱柱,
是直三棱柱,![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,且
的中点,且![]() ,则
,则![]() 与
与![]() 所成角的余弦值是(
所成角的余弦值是(![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
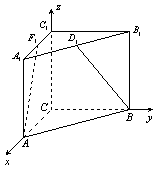 解:建立空间直角坐标系如图,设
解:建立空间直角坐标系如图,设![]() ,
,![]() ,
,![]() ,
,![]() 。
。
于是![]() ,
,![]() ,则
,则![]() 。
。
 所以
所以![]() 与
与![]() 所成角的余弦值是
所成角的余弦值是![]() 。
。
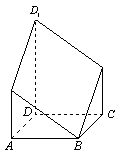
*16、图中多面体是经过正四棱柱底面顶点![]() 作截面
作截面![]() 而截得的。已知
而截得的。已知![]() ,截面
,截面![]() 与底面
与底面![]() 成
成![]() 的二面角,
的二面角,![]() ,则这个多面体的体积为(
,则这个多面体的体积为(![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
 解:过
解:过![]() 作
作![]() ,
,![]() ,联结
,联结![]() 、
、![]() 。
。
取![]() 中点
中点![]() ,联结
,联结![]() 、
、![]() 。
。
![]() 平面
平面![]() ,所以截面
,所以截面![]() 与平面
与平面![]() 所成的二面角为
所成的二面角为![]() 。
。
![]() ,
,![]() 为
为![]() 中点,
中点,![]() 。
。
![]() ,
,![]() ,即
,即![]() ,则
,则![]() 。
。
![]() 。
。
![]() ,同理得
,同理得![]() 。
。
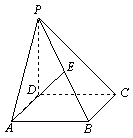 于是多面体体积
于是多面体体积![]() 。
。
三、解答题
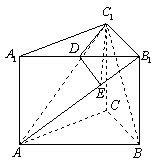
17、如图,![]() 垂直正方形
垂直正方形![]() 所在平面,
所在平面,![]() ,
,![]() 是
是![]() 的中点,向量
的中点,向量![]() 、
、![]() 的夹角为
的夹角为![]() 。
。
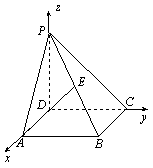 (1)建立适当的坐标系,求点
(1)建立适当的坐标系,求点![]() 的坐标;
的坐标;
(2)在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() 。
。
解:(1)以![]() 、
、![]() 、
、![]() 所在的直线分别为
所在的直线分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴建立空间直角坐标系如图,则
轴建立空间直角坐标系如图,则![]() ,
,![]() 。设
。设![]() (
(![]() ),
),![]() 。
。
于是![]() ,
,![]() 。
。
由题意得,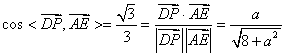 ,
,
解得![]() 或
或![]() (舍)。
(舍)。
所以点![]() 的坐标为
的坐标为![]() 。
。
(2)设点![]() 的坐标为
的坐标为![]() ,则
,则![]() 。
。
要使![]() 平面
平面![]()
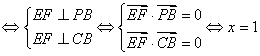 。
。
所以点![]() 的坐标为
的坐标为![]() ,即点
,即点![]() 为
为![]() 的中点。
的中点。
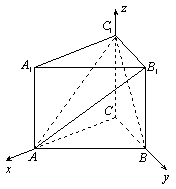
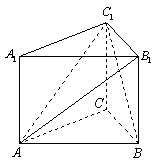 18、直三棱柱
18、直三棱柱![]() 中,
中,![]() ,
,![]() 。
。
(1)证明:![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离;
的距离;
(3)求二面角![]() 的大小。
的大小。
解:(1)![]()
![]()
![]() ,
,![]() 。
。
(2)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
因为![]() ,
,![]() ,又
,又![]() 平面
平面![]() ,则
,则![]() ,
,
![]() 平面
平面![]() 。
。
同理得![]() 平面
平面![]() ,所以
,所以![]() 。
。
于是![]() 。
。
因为![]() ,
,![]() ,
,
所以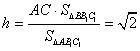 。
。
 故点
故点![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
(3)取![]() 中点
中点![]() ,联结
,联结![]() ,过
,过![]() 作
作![]() 交于
交于![]() ,联结
,联结![]() 。
。
![]() 是等腰三角形,
是等腰三角形,![]() 。
。
又![]() 平面
平面![]() ,
,![]() ,所以
,所以![]() 平面
平面![]() 。
。
于是![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,得
,得![]() 。
。
因此,![]() 为二面角
为二面角![]() 的平面角。
的平面角。
![]() ,
,![]() ,
,
![]() ,即
,即![]() 。
。
所以二面角![]() 的大小为
的大小为![]() 。
。
 另解:(空间向量)
另解:(空间向量)
(1)建立空间直角坐标系如图,则![]() ,
,![]() ,
,![]() ,
,![]() 。
。
于是![]() ,
,![]() 。
。
则![]() ,所以
,所以![]() 。
。
(2)设![]() 是平面
是平面![]() 的法向量,
的法向量,
由![]() ,
,![]() ,得
,得
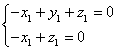 ,所以
,所以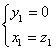 。
。
令![]() ,则
,则![]() 。
。
又![]() ,所以
,所以![]() 到平面
到平面![]() 的距离
的距离 。
。
(3)设![]() 是平面
是平面![]() 的法向量,
的法向量,
由![]() ,
,![]() 得
得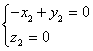 ,所以
,所以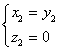 。
。
令![]() ,则
,则![]() 。
。
因为![]() ,
,
所以,二面角![]() 的平面角的大小为
的平面角的大小为![]() 。
。
19、已知数列![]() 满足
满足![]() (
(![]() ,且
,且![]() ),其前
),其前![]() 项和
项和![]() 。
。
(1)求证:![]() 为等比数列;
为等比数列;
(2)记![]() (
(![]() ),
),![]() 为数列
为数列![]() 的前
的前![]() 项和。当
项和。当![]() 时,求
时,求![]() 。
。
证明:(1)当![]() 时,
时,![]() ,
,
整理得![]() ,
,![]() ,所以
,所以![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列。
为公比的等比数列。
于是![]() 。
。
(2)因为![]() ,
,![]() 。
。
当![]() 时,
时,![]() ,
,
![]() ,
,
两式相减得,![]()
![]()
![]() ,又
,又![]() ,
,
所以,![]()
![]() 。
。
20、已知数列![]() 满足
满足![]() ,其中
,其中![]() 为其前
为其前![]() 项的和,
项的和,![]() 。
。
(1)证明:数列![]() 的通项公式为
的通项公式为![]() ;
;
(2)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)是否存在无限集合![]() 为正整数}, 总有
为正整数}, 总有![]() <
<![]() 成立;若存在,请找出一个这样的集合;若不存在,请说明理由。
成立;若存在,请找出一个这样的集合;若不存在,请说明理由。
证明(1)当![]() 时,
时,![]() ,
,
整理得![]() 。
。
于是![]() ,
,
![]()
![]() 。
。
(2)![]() ,
,
![]() 。
。
(3)要使![]() ,即
,即![]() ,只需
,只需![]() 即可。
即可。
所以, ![]() 。
。