高二数学第二学期六校联考试卷
命题学校:掘港高级中学 命题人:高二数学备课组
一、填空题(共14题,每题5分合计70分)
1.命题:“若![]() 不为零,则
不为零,则![]() 都不为零”的逆否命题是 ▲ 。
都不为零”的逆否命题是 ▲ 。
2.命题“对一切非零实数![]() ,总有
,总有![]() ”的否定是 ▲ 它是 ▲ 命题
”的否定是 ▲ 它是 ▲ 命题
3. 有下列四个命题:
①、命题“若![]() ,则
,则![]() ,
,![]() 互为倒数”的逆命题; ②、命题“面积相等的三角形全等”的否命题;
互为倒数”的逆命题; ②、命题“面积相等的三角形全等”的否命题;
③、命题“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④、命题“若![]() ,则
,则![]() ”的逆否命题。
”的逆否命题。
其中是真命题的是 ▲ (填上你认为正确的命题的序号)。
4. 下列四个命题中
①“![]() ”是“函数
”是“函数![]() 的最小正周期为
的最小正周期为![]() ”的充要条件;
”的充要条件;
②“![]() ”是“直线
”是“直线![]() 与直线
与直线![]() 相互垂直”的充要条件;
相互垂直”的充要条件;
③ 函数![]() 的最小值为
的最小值为![]()
其中假命题的为 ▲(将你认为是假命题的序号都填上)
5. 曲线![]() 在点
在点![]() 处的切线倾斜角为 ▲ ;
处的切线倾斜角为 ▲ ;
6.设函数![]() ,若
,若![]() 为奇函数,则
为奇函数,则![]() = ▲
= ▲
7.已知![]() 有极大值和极小值,则
有极大值和极小值,则![]() 的取值范围为 ▲
的取值范围为 ▲
8.已知函数![]() 的图象与
的图象与![]() 轴切于点
轴切于点![]() ,则
,则![]() 的极大值、极小值依次为 ▲
的极大值、极小值依次为 ▲
9.已知函数![]() 在
在![]() 处分别取得最大值与最小值,又数列
处分别取得最大值与最小值,又数列
![]() 为等差数列,则
为等差数列,则![]() 的值为 ▲
的值为 ▲
10.物体运动方程为![]() ,则
,则![]() 时的瞬时速度为 ▲
时的瞬时速度为 ▲
11.直线![]() 与函数
与函数![]() 的图像有相异的三个公共点,则
的图像有相异的三个公共点,则![]() 的取值范围是__ ▲
的取值范围是__ ▲
12.“![]() ”是“
”是“![]() 有且仅有整数解”的____▲______条件。
有且仅有整数解”的____▲______条件。
13.已知![]() 、
、![]() 是不同的两个平面,直线
是不同的两个平面,直线![]() ,命题
,命题![]() 无公共点;命题
无公共点;命题![]() , 则
, 则![]() 的 ▲ 条件
的 ▲ 条件
14.函数![]() 的导数为___ ▲ .
的导数为___ ▲ .
二、解答题
15.(本题14分)
设函数![]() 的定义域为A,若命题
的定义域为A,若命题![]() 有且只有一个为真命题,求实数a的取值范围.
有且只有一个为真命题,求实数a的取值范围.
16. (本题14分)
已知下列三个方程:![]() 至少有一个方程有实数根,求实数
至少有一个方程有实数根,求实数![]() 的取值范围。
的取值范围。
17.(本题15分)
如图,一矩形铁皮的长为
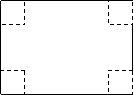 |
18.(本题15分)
命题![]() 方程
方程![]() 有两个不等的正实数根,命题
有两个不等的正实数根,命题![]() 方程
方程![]() 无实数根。若“
无实数根。若“![]() 或
或![]() ”为真命题,求
”为真命题,求![]() 的取值范围。
的取值范围。
19.( 本小题满分16分)
已知函数![]() 。
。
(1)求函数![]() 的图像在
的图像在![]() 处的切线方程;
处的切线方程;
(2)求![]() 的最大值;
的最大值;
(3) 设实数![]() ,求函数
,求函数![]() 在
在![]() 上的最小值
上的最小值
20.(本小题满分16分)
已知![]() ,点
,点![]() .
.
(Ⅰ)若![]() ,求函数
,求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)若函数![]() 的导函数
的导函数![]() 满足:当
满足:当![]() 时,有
时,有![]()
![]() 恒成立,求函数
恒成立,求函数![]() 的解析表达式;
的解析表达式;
(Ⅲ)若![]() ,函数
,函数![]() 在
在![]() 和
和![]() 处取得极值,且
处取得极值,且![]() ,证明:
,证明:![]() 与
与![]() 不可能垂直。
不可能垂直。
(答案)
一、填空题
1、若![]() 至少有一个为零,则
至少有一个为零,则![]() 为零
为零
2、存在![]() 且
且![]() 使得
使得![]() 真
真
3、①,②,③ 4、①,②,③ 5、![]() 6、
6、![]()
7、![]() 8、
8、![]() ;
;![]() 9、
9、![]() 10、
10、![]()
11、(-2,2) 12、必要条件 13、必要
14、![]()
二、解答题
15、解:![]() …………1分
…………1分
若![]() …………3分
…………3分
若![]() …………5分
…………5分
若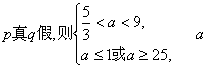 无解; …………8分
无解; …………8分
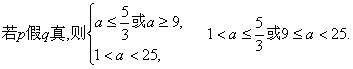 …………12分
…………12分
综上,![]() …………14分
…………14分
16、解:假设三个方程:![]() 都没有实数根,
都没有实数根,
3分
则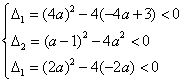 ,
6分
,
6分
即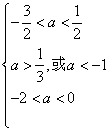 , 9分
, 9分
得![]() 12分
12分
![]() 。 14分
。 14分
17、
解:设小正方形的边长为![]() 厘米,(0<x<5)
2分
厘米,(0<x<5)
2分
则盒子底面长为![]() ,宽为
,宽为![]() (5-2x>0)
4分
(5-2x>0)
4分
![]() 6分
6分
![]() ,
9分
,
9分
![]() (舍去)
11分
(舍去)
11分
![]() ,在定义域内仅有一个极大值,
14分
,在定义域内仅有一个极大值,
14分
![]() 15分
15分
18、
解:“![]() 或
或![]() ”为真命题,则
”为真命题,则![]() 为真命题,或
为真命题,或![]() 为真命题,或
为真命题,或![]() 和
和![]() 都是真命题 3分
都是真命题 3分
当![]() 为真命题时,则
为真命题时,则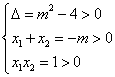 ,得
,得![]() ; 6分
; 6分
当![]() 为真命题时,则
为真命题时,则![]() 9分
9分
当![]() 和
和![]() 都是真命题时,得
都是真命题时,得![]() 12分
12分
![]() 15分
15分
19、解(1)![]() 定义域为
定义域为![]() 1分
1分
![]() 3分
3分
![]() 4分
4分
又
![]() 5分
5分
![]() 函数
函数![]() 的在
的在![]() 处的切线方程为:
处的切线方程为:
![]() ,即
,即![]() 6分
6分
(2)令![]() 得
得![]()
![]() 当
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数
8分
上为增函数
8分
当![]() 时,
时,![]() ,在
,在![]() 上为减函数
10分
上为减函数
10分
![]() 12分
12分
(3)![]()
![]() ,由(2)知:
,由(2)知:
![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
![]()
![]() 在
在![]() 上的最小值
上的最小值![]() 13分
13分
![]() 14分
14分
![]() 当
当![]() 时,
时,![]()
![]()
![]() 15分
15分
当![]() 时
时![]() ,
,![]()
![]() 16分
16分
20、
解:(Ⅰ) ![]() ,
, ![]()
令![]() 得
得![]() ,解得
,解得![]()
故![]() 的增区间
的增区间![]() 和
和![]() 4分
4分
(Ⅱ)![]() (x)=
(x)=![]()
当x∈[-1,1]时,恒有![]() (x)≤
(x)≤![]() . 5分
. 5分
故有![]() ≤
≤![]() (1)≤
(1)≤![]() ,
,![]() ≤
≤![]() (-1)≤
(-1)≤![]() ,
,
及![]() ≤
≤![]() (0)≤
(0)≤![]() ,
6分
,
6分
即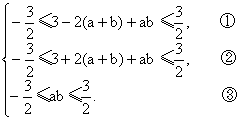 ………………………8分
………………………8分
①+②,得![]() ≤
≤![]() ≤
≤![]() ,………8分 又由③,得
,………8分 又由③,得![]() =
=![]() ,将上式代回①和②,得
,将上式代回①和②,得![]() 故
故![]()
![]() .
10分
.
10分
(Ⅲ)假设![]() ⊥
⊥![]() ,即
,即![]()
![]() =
=![]() 11分
11分
故(s-a)(s-b)(t-a)(t-b)=-1 [st-(s+t)a+a2][st-(s+t)b+b2]=-1,……………11分
由s,t为![]() (x)=0的两根可得,s+t=
(x)=0的两根可得,s+t=![]() (a+b), st=
(a+b), st=![]() , (0<a<b)
, (0<a<b)
从而有ab(a-b)2=9.………12分
这样![]()
即 ![]() ≥2
≥2![]() ,这与
,这与![]() <2
<2![]() 矛盾. ………………………14分
矛盾. ………………………14分
故![]() 与
与![]() 不可能垂直. ………………………16分
不可能垂直. ………………………16分