高二数学第二学期末考试模拟2
班级 姓名 学号 20062
一,选择题(共10个小题,共计50分)
1. (![]() )6+(
)6+(![]() )6 的值为
( )
)6 的值为
( )
A.2i B.-2i C.0 D.i
2,在所有的两位数(10~99)中,任取一个数,则这个数能被2或3整除的概率是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 直线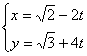 (t为参数)的斜率K的值是勤
( )
(t为参数)的斜率K的值是勤
( )
A. ![]() B.
-
B.
-![]() C. 2
D. -2
C. 2
D. -2
4. 5个人站成一排,其中甲不在左端也不和乙相邻的排法种数是 ( )
A.
48
B
5. 设(2x+![]() )
)![]() =
=![]() 则
则![]() 值为 (
)
值为 (
)
A. 16
B. -
6. 长方体ABCD—A1B
AA1=2AB,则CE与BF所成角的余弦值是 ( )![]()
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
7. 极坐标方程4![]() sin2
sin2![]() =1所表示的曲线是
(
)
=1所表示的曲线是
(
)
(A)圆 (B)椭圆 (C)双曲线的一支 (D)抛物线
8, 设P(x,y)是曲线C:x2+y2+4x+3=0上任意一点,则![]() 的取值范围是
( )
的取值范围是
( )
A.[-![]() ] B.(-∞,-
] B.(-∞,-![]() )∪[
)∪[![]() ,+∞)
,+∞)
C.[-![]() ] D.(-∞,-
] D.(-∞,-![]() )∪[
)∪[![]() ,+∞)
,+∞)
9, 设随机变量![]() ~B(n,p),且E
~B(n,p),且E![]() =1.6,D
=1.6,D![]() =1.28, 则有
( )
=1.28, 则有
( )
A,n=8, p=0.2 , B,n=4, p=
10. 设随机变量![]() 服从正态分布
服从正态分布![]() ,则下列结论不正确的是:
( )
,则下列结论不正确的是:
( )
A.![]() B,
B,![]()
C,![]() D,
D,![]()
二,填空题(共5个小题,共计25分)
11.实数x、y满足(1-i)x+(1+i)y=2,则 xy 的值是 __________.
12. 设![]() 是一个离散型随机变量,其分布列如下:
是一个离散型随机变量,其分布列如下: ![]()
| ξ | -1 | 0 | 1 |
| P | 0.5 | 1 | q2 |
则q= ![]()
13. 不等式![]() <1的解集为(-∞ ,1)∪(2,+∞),则a= .
<1的解集为(-∞ ,1)∪(2,+∞),则a= .
14,在极坐标系中,直线![]() 的方程为ρsinθ=3,则点(2,
的方程为ρsinθ=3,则点(2,![]() )到直线
)到直线![]() 的距离为___________.
的距离为___________.
15,实验测得四组(x,y)的值是 (2,3),(3,4),(4,5),(5,6),则y与x之间的回归直线的方程
是_____ _
(参考公式:![]() =
=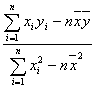 ,â=
,â=![]() -
-![]()
![]() , 其中
, 其中 ![]() ,
,![]() )
)
三,解答题(共6个大题,共计75分)
16. (12分)椭圆的参数方程为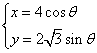 (
(![]() ----参数),在椭圆上找一点P,使P点到直
----参数),在椭圆上找一点P,使P点到直
线![]() 的距离d最小, 求点P的坐标和d的最小值,
的距离d最小, 求点P的坐标和d的最小值,
17. (12分)二项式![]() 展开式中第五项的二项式系数是第三项系数的4倍.
展开式中第五项的二项式系数是第三项系数的4倍.
求:(1)n ; (2)展开式中的所有的有理项。
18. (13分)男运动员6名,女运动员4名,其中男女队长各1人,从中选5人外出比赛,下列情形各
有多少种选派方法,
⑴男3名,女2名 ⑵队长至少有1人参加
⑶至少1名女运动员 ⑷既要有队长,又要有女运动员
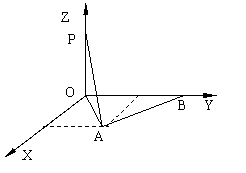
19.(12分)已知点![]() ,对于
,对于![]() 轴正半轴上任意一点
轴正半轴上任意一点![]() ,在
,在![]() 轴上是否存在一点
轴上是否存在一点![]() ,
,
使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 点的坐标;若不存在,说明理由。
点的坐标;若不存在,说明理由。
 |
20, (12分)2008年北京奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌,保守估计中国乒乓球男队获得每枚金牌的概率均为![]() ,中国乒乓球女队一枚金牌的概率均为
,中国乒乓球女队一枚金牌的概率均为![]() ;(1)求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;
;(1)求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率;
(2)记中国乒乓球队获得金牌的数为![]() ,按此估计
,按此估计![]() 的分布列和数学期望
的分布列和数学期望![]() 。
。
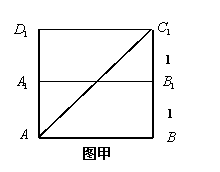
21, (14分)如图,在长方体![]() 中,
中,![]() ,点
,点![]() 在棱
在棱![]() 上移动,小蚂蚁从点
上移动,小蚂蚁从点![]() 沿长方体的表面爬到点
沿长方体的表面爬到点![]() ,所爬的最短路程为
,所爬的最短路程为![]() 。
。
(Ⅰ)求证:![]() ⊥
⊥![]() ;
;
(Ⅱ)求![]() 的长度;
的长度;
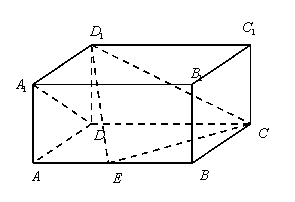 (Ⅲ)在线段
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() 。若存在,确定点
。若存在,确定点![]() 的
的
位置;若不存在,请说明理由。
2007—2008高二第二学期期末考试模拟2
参考解答
一, C C D B A D D C A C
二, 11; 1 12; ![]() 13;
13;![]()
14; 2 15; ![]() = x+1
= x+1
三,解答题:
16. (12分)设椭圆上的动点P(4cos![]() , 2
, 2![]() sin
sin![]() ), 由点线距离公式得,
), 由点线距离公式得,
则 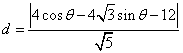
![]()
当![]() ,即
,即![]() = -
= -![]() 时
时
![]() , 此时所求点为 P
, 此时所求点为 P![]() 。
。
17. (12分)
解:(1)二项式的通项
![]() ………2分
………2分
依题意,![]() ………4分
………4分
解得 n=6 ……….7分
(2)由(1)得![]() ,当r=0,3,6时为有理项,…………10分
,当r=0,3,6时为有理项,…………10分
故有理项有![]() ,
,![]() ,
,![]() ……………..12分
……………..12分
18. (13分)
解: ⑴从10名运动员中选5人参加比赛,其中男3人,女2人的选法有C![]() C
C![]() =120 (种)
=120 (种)
⑵从10名运动员中选5人参加比赛,其中队长至少有1人参加的选法有
C![]() C
C![]() +C
+C![]() C
C![]() =140+56=196 (种)
=140+56=196 (种)
⑶从10名运动员中选5人参加比赛,其中至少有1名女运动员参加的选法有
C![]() -C
-C![]() =2461 (种)
=2461 (种)
⑷从10名运动员中选5人参加比赛,既要有队长又要有女运动员的选法有
C![]() -C
-C![]() -C
-C![]() =191 (种)
=191 (种)
19.(12分)解:如图,若![]() 恒成立,则
恒成立,则![]() 平面
平面![]() ,所以
,所以![]() ,
,
设![]() ,则有
,则有![]() ,
,
由![]() ,得
,得![]() ,解得
,解得![]() ,
,
所以存在这样的点![]() ,当点
,当点![]() 为
为![]() 时,
时,![]() 恒成立。
恒成立。
20, (12分)
(1)设中国乒乓球男队获0枚金牌,女队获1枚金牌为事件![]() ,中国乒乓球男队获1枚金牌,
,中国乒乓球男队获1枚金牌,
女队获2枚金牌为事件![]() ,那么,
,那么,
![]() ==
==![]()
![]() …(4分)
…(4分)
(2)根据题意中国乒乓球队获得金牌数是一随机变量![]() ,它的所有可能取值为0,1,2,3,4
,它的所有可能取值为0,1,2,3,4
(单位:枚)那么![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ……………………………………………………(8分)
……………………………………………………(8分)
则概率分布为:
|
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
|
………………………………………………………………………………………(10分)
那么,所获金牌的数学期望![]() (枚)
(枚)
答:中国乒乓球队获得金牌数的期望为![]() 枚。…….(12分)
枚。…….(12分)
21, (14分) 解法一 (传统法)
(Ⅰ)证明:连结![]() ,由长方体的性质可知:
,由长方体的性质可知:![]() ⊥平面
⊥平面![]() ,
,
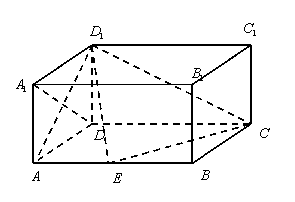 ∵
∵![]() 平面
平面![]() , ∴
, ∴![]() ⊥
⊥![]() ,
2分
,
2分
又∵![]() ,∴
,∴![]() ⊥
⊥![]() ,
,
![]() , ∴
, ∴![]() ⊥平面
⊥平面![]() , 4分
, 4分
![]() 平面
平面![]() ,∴
,∴![]() ⊥
⊥![]() 。 5分
。 5分
(Ⅱ)设![]() ,∵四边形
,∵四边形![]() 是正方形,∴小蚂蚁从点
是正方形,∴小蚂蚁从点![]() 沿长方体的表面爬到点
沿长方体的表面爬到点![]() 可能有
可能有
两种途径。
如图甲的最短路程为![]() ,
,
如图乙的最短路程为![]() ,
7分
,
7分
![]()
![]() ,
,
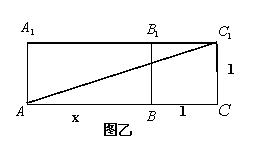
![]() 。
9分
。
9分
(Ⅲ)假设存在连结![]() ,设
,设![]() ,
,
过点![]() 在平面
在平面![]() 内作
内作![]() ⊥
⊥![]() ,连结
,连结![]() ,
,
则![]() 为二面角
为二面角![]() 的平面角,
的平面角,![]() ,
11分
,
11分
![]() 在
在![]() 内,
内,![]() ,而
,而![]() ,
,
 即
即![]() ,解得
,解得![]() ,
,
即存在![]() 点,且与点
点,且与点![]() 距离为
距离为![]() 时,
时,
二面角![]() 的大小为
的大小为![]() 。
14分
。
14分
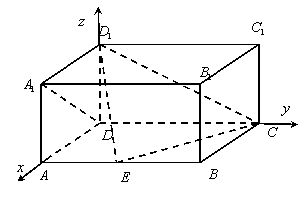
解法二:(向量法)
(Ⅰ)如图以D为原点建立空间坐标系,如图; 1分
设![]() ,则
,则![]() ,
,![]() ,
,![]() 。
2分
。
2分
![]() ,
,![]() 。
4分
。
4分
(Ⅱ)同解法一 9分
(Ⅲ)假设存在,平面![]() 的法向量
的法向量![]() ,
,![]() ,
10分
,
10分
设平面![]() 的法向量
的法向量![]() ,
,
则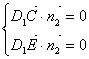 即
即![]() ,
,
取![]() ,解得:
,解得:![]()
![]() ,
12分
,
12分
由题意得: ,
,
解得:![]() (舍去),
(舍去),
即存在![]() 点,且与点
点,且与点![]() 距离为
距离为![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() 。 14分
。 14分