高二第一学期（理科）数学期末考试卷

高二第一学期（理科）数学期末考试卷

一、选择题（本大题共11小题，每小题3分，共33分）

1、与向量平行的一个向量的坐标是（　　）

　　　 A．（，1，1）　 　　　　　　　　　　　　　　　　 B．（－1，－3，2）　

　　　 C．（－，，－1）　 　　　　　　　　　　　 D．（，－3，－2）

2、设命题：方程的两根符号不同；命题：方程的两根之和为3，判断命题“”、“”、“”、“”为假命题的个数为( 　 )

A．0　　　　　B．1  　　　　　C．2　 　　　　D．3

3、“a＞b＞0”是“ab＜”的 （　　　 ）

A．充分而不必要条件　　　 　　　B．必要而不充分条件

C．充要条件　　　　　　　　　　 D．既不充分也不必要条件

4、椭圆的焦距为2，则的值等于　（ 　　 ）.

A．5　　　 B．8  　　 C．5或3　　　　 D．5或8

5、已知空间四边形OABC中，，点M在OA上，且OM=2MA，N为BC中点，则=（　　）

　　　 A．　　 　　　　　　　　　　　　　B．　　　　　　　　　　　

　　　 C．　　 　　　　　　 　　 D．

6、抛物线上的一点M到焦点的距离为1，则点M的纵坐标为（　　）

A．　　　　　　  B．　　　　　　 C．　　　　　　 D．0

7、已知对称轴为坐标轴的双曲线有一条渐近线平行于直线x＋2y－3＝0，则该双曲线的离心率为（　　　）

 A.5或　　　  B.或　　   C. 或 　　D.5或

8、若不等式x－1 <a成立的充分条件是0<x<4,则实数a的取值范围是 (　　　)

　 A．a1　　　 B．a3　　　　  C．a1　　　　 D．a3

9、已知，则的最小值为　 （　　）

　　　 A．　　　　　B．　　　 　　　C．　 　　　　D．

10、已知动点P(x、y)满足10＝3x＋4y＋2，则动点P的轨迹是　　 （  ）

　　A．椭圆　　　　　　　 B．双曲线　　C．抛物线　　　　　　　　 D．无法确定

11、已知P是椭圆上的一点，O是坐标原点，F是椭圆的左焦点且，则点P到该椭圆左准线的距离为（　　　 ）

A.6　　　　  B.4　　　　  C.3　　　　　  D.

安庆一中2007——2008学年度第一学期高二（理科）

数学期末考试卷

一、选择题（本大题共11小题，每小题3分，共33分）

题号	1	2	3	4	5	6	7	8	9	10	11
答案

二、填空题（本大题共4小题，每小题3分，共12分）

12、命题：的否定是　　　　　　　　　　　　　 

13、若双曲线 的左、右焦点是、，过的直线交左支于A、B两点，若AB=5，则△AF₂B的周长是　　　　　　  .

14、若，，则为邻边的平行四边形的面积为　　　　　　　 ．

15、以下四个关于圆锥曲线的命题中：

　　①设A、B为两个定点，k为正常数，，则动点P的轨迹为椭圆；

　　②双曲线与椭圆有相同的焦点；

　　③方程的两根可分别作为椭圆和双曲线的离心率；

　　④和定点及定直线的距离之比为的点的轨迹方程为．

其中真命题的序号为　　　　_________．

三、解答题（本大题共6小题，共55分）

16、（本题满分8分）已知命题p：方程表示焦点在y轴上的椭圆，命题q：双曲线的离心率，若只有一个为真，求实数的取值范围．

17、（本题满分8分）已知棱长为1的正方体ABCD－A₁B₁C₁D₁，试用向量法求平面A₁BC₁与平面ABCD所成的锐二面角的余弦值。

18、（本题满分8分）

（1）已知双曲线的一条渐近线方程是，焦距为，求此双曲线的标准方程；

（2）求以双曲线的焦点为顶点，顶点为焦点的椭圆标准方程。

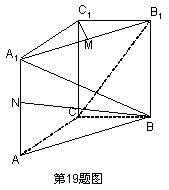19、（本题满分10分）如图所示，直三棱柱ABC—A₁B₁C₁中，CA=CB=1，∠BCA=90°，棱AA₁=2，M、N分别是A₁B₁、A₁A的中点.

（1）求的长；

（2）求cos< >的值；

（3）求证：A₁B⊥C₁M.

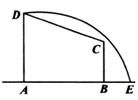20、（本题满分10分）如图所示，在直角梯形ABCD中，AD＝3，AB＝4，BC＝，曲线段DE上任一点到A、B两点的距离之和都相等．

（1）建立适当的直角坐标系，求曲线段DE的方程；

（2）过C能否作一条直线与曲线段DE相交，且所

得弦以C为中点，如果能，求该弦所在的直线

的方程；若不能，说明理由．

21、（本题满分11分）若直线l：与抛物线交于A、B两点，O点是坐标原点。

(1)当m=－1,c=－2时，求证：OA⊥OB；

 (2)若OA⊥OB，求证：直线l恒过定点；并求出这个定点坐标。

(3)当OA⊥OB时，试问△OAB的外接圆与抛物线的准线位置关系如何？证明你的结论。

高二数学（理科）参考答案：

1、C　2、C 　3、A　  4、C　5、B　 6、B  7、B 　8、D 　9、C　 10、A　

11、D

12、　　  13、18　　　　14、　　　 15、②③

16、p:0<m<　　 q:0< m <15　　 p真q假，则空集；p假q真，则　

故m的取值范围为　　

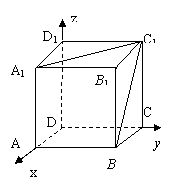
17、如图建立空间直角坐标系，＝（－1，1，0），＝（0，1，－1）

　　设、分别是平面A₁BC₁与平面ABCD的法向量，

 由　　　　　可解得＝（1，1，1）

易知＝（0，0，1），

所以，＝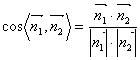

所以平面A₁BC₁与平面ABCD所成的锐二面角的余弦值为。

18、（1）或；（2）.

19、如图，建立空间直角坐标系O—xyz.

（1）依题意得B（0，1，0）、N（1，0，1）

∴ =.

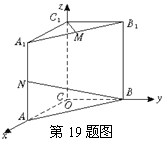（2）依题意得A₁（1，0，2）、B（0，1，0）、C（0，0，0）、B₁（0，1，2）

∴=（1，－1，2），=（0，1，2），·=3，=，=

∴cos<，>=.

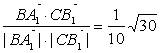（3）证明：依题意，得C₁（0，0，2）、M（，2），=（－1，1，－2），

=（，0）.∴·=－+0=0，∴⊥，

∴A₁B⊥C₁M.

20、（1）以直线AB为x轴，线段AB的中点为原点建立直角坐标系，

则A（－2，0），B（2，0），C（2， ），D（－2，3）．

依题意，曲线段DE是以A、B为焦点的椭圆的一部分．

∴所求方程为

　 （2）设这样的弦存在，其方程为：

　　

得

设弦的端点为M（x₁，y₁），N（x₂，y₂），则由

∴弦MN所在直线方程为验证得知，

这时适合条件．

故这样的直线存在，其方程为

21、解：设A(x₁,y₁)、B(x₂,y₂)，由得

可知y₁+y₂=－2m　y₁y₂=2c　 ∴x₁+x₂=2m²—2c　x₁x₂= c²,

(1)　　当m=－1,c=－2时，x₁x₂ +y₁y₂=0 所以OA⊥OB.

(2)　　当OA⊥OB时，x₁x₂ +y₁y₂=0 于是c²+2c=0 ∴c=－2(c=0不合题意),此时，直线l：过定点(2,0).

(3)　　由题意AB的中点D(就是△OAB外接圆圆心)到原点的距离就是外接圆的半径。

而(m²—c+)²－[(m²—c)²+m² ]=　由(2)知c=－2　

∴圆心到准线的距离大于半径,故△OAB的外接圆与抛物线的准线相离。