高二数学下学期期末复习题（二） 08年07月
班级 学号 得分
一、填空题（每题5分，共14题，计70分）
1.已知集合
，则
。
2. 定义运算
，则符合条件
=0的复数z的共轭复数所对
应的点在第 象限。
3.已知
、
的取值如下表所示：
|
| 0 | 1 | 3 | 4 |
|
| 2.2 | 4.3 | 4.8 | 6.7 |
从散点图分析，与线性相关，且
，则
。
4. 偶函数
单调递减，若A、B是锐角三角形的两个内角，则
与
的大小关系为 。
5. 设函数
的最大值为M ，最小值为m，则M+m=
。
6. 若不等式
有解，则实数a的范围是 。
7. 已知
，则
.
8. 已知命题p: 函数
的值域为R。命题q：函数
是减函数。若p或q为真命题，p且q为假命题，则实数a的取值范围是
。
9. 已知函数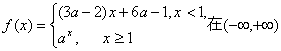
上单调递减，那么实数a的取值范围是
。
10. 函数
在（0，2
）内的单调增区间为
．
11.定义运算a*b为：a*b=
，例如，1*2=1，则函数
的值域为 .
12.若
为整数，则整数
的个数为
。
13. 函数f(x)=
(
) 的值域是 。
14. 已知定义域为
的函数
，对任意
，存在正数
，都有
成立，则称函数是上的“有
界函数”。已知下列函数：①
；②
；③
；
④
，其中是“有界函数”的是
（写出所有满足要求的函数的符号）．
二、解答题（共6小题，计90分）
15.已知复数
，
满足
，
，其中
是虚数单位，
，若
，求
的取值范围。
16. 已知函数
。
（1）当
时，求函数f(x)的最大值和最小值；
（2）求
的取值范围，使y=f(x)在区间
上是单调函数。
17. 已知函数
的图象关于直线
对称，且
若
时，求
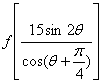的值.
18. 若
，若函数
的图象与直线
(
为常数)相切，并且切点的横坐标依次成公差为
的等差数列。
（1）求
的值；
（2）将
的图象向左平移
个单位，再将得到的图象的横坐标变为原来的2倍（纵坐标不变）后得到
的图象；若函数
的图象与
的图象的交点的横坐标成等比数列，试求的值。
19. 已知函数
，存在正数
，使得的定义域和值域相同．
（1）求非零实数的值；
（2）若函数
有零点，求的最小值．
20. 已知
.
⑴ 求函数在
上的最小值；
⑵ 对一切
，
恒成立，求实数的取值范围；
⑶ 证明对一切，都有
成立.
答案 08年06月
1. {-1，1} 2.一 
5.2
6. （0，1）
7. 
8. 1＜a＜2
9. 
10. 
11.
12.
3
13. [-1,0] 14. ①②④
15.
16. （1）
，
；（2）
17. 解：∵
又∵
∴
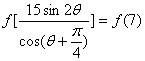
由题意关于直线x=3对称
∴
即：
18. （1）
；（2）
19. 解：（1）若
，对于正数，的定义域为
，但 的值域
，故
，不合要求． --------------------------2分
若
，对于正数，的定义域为
． -----------------3分
由于此时
，
故函数的值域
．
------------------------------------6分
由题意，有
，由于
，所以
．------------------8分
(2) 方程变形为
，有解，即
的极小值小于等于0，得
。
20. 解答：⑴ 
，当
，
，单调递减，当
，
，单调递增.
① 
，t无解；
② 
，即
时，
；
③ 
，即
时，在
上单调递增，
；
所以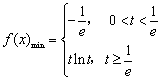
.
⑵ 
，则
，设
，则
，
，
，
单调递增，
，
，单调递减，所以
，因为对一切，恒成立，所以
；
⑶ 问题等价于证明
，由⑴可知
的最小值是
，当且仅当
时取到，设
，则
，易得
，当且仅当
时取到，从而对一切，都有成立.