高二数学下学期期末复习题（三） 08年07月
班级 学号 得分
一、填空题
1．（江西卷1）在复平面内，复数
对应的点位于第 象限．
2．（山东卷2）设z的共轭复数是
，或z+=4,z·＝8，则
等于 ．
3.（福建卷4)函数
,若
,则
的值为 ．
4．集合
，
则
．
5．(山东文)给出命题：若函数
是幂函数，则函数的图象不过第四象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是 ．
6.（重庆卷13)已知
(a>0) ，则
.
7．（广东卷7）设
，若函数
，
有大于零的极值点，则
的取值范围是
．
8．（广东卷12）已知函数
，，则
的最小正周期是
．
9．（全国一9）设奇函数在
上为增函数，且
，则不等式
的解集为
．
10.（四川卷11）设定义在
上的函数
满足
，若
，则
．
11．（全国二8）若动直线
与函数
和
的图像分别交于
两点，则
的最大值为 ．
12．（四川卷10）设
，其中
，则
是为偶函数的
条件．
13．（上海卷11）方程
的解可视为函数
的图像与函
的图像交点的横坐标，若
的各个实根
所对应的点
均在直线
的同侧，则实数的取值范围是 ．
14．（天津卷10）设
，若对于任意的
，都有
满足方程
，这时的取值集合为
．
二、解答题
15．已知集合
，集合
．
（1）若
，求实数
的取值范围；
（2）若
，求实数的取值范围．
16．（山东卷17）
已知函数f(x)＝
为偶函数，且函数
图象的两相邻对称轴间的距离为
（Ⅰ）求
的值；
（Ⅱ）将函数的图象向右平移
个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数
的图象，求
的单调递减区间
17．已知定义域为R的函数
是奇函数，若对任意的tÎR，不等式
恒成立，（1）求
的值；（2）求
的取值范围．
18．（湖北卷20）
水库的蓄水量随时间而变化，现用
表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于的近似函数关系式为
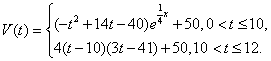
（Ⅰ）该水库的蓄求量小于50的时期称为枯水期.以
表示第1月份（
）,同一年内哪几个月份是枯水期？
（Ⅱ）求一年内该水库的最大蓄水量（取
计算）.
19．已知函数
（
），其中
．
（Ⅰ）当
时，讨论函数的单调性；
（Ⅱ）若函数仅在
处有极值，求的取值范围；
（Ⅲ）若对于任意的
，不等式
在
上恒成立，求
的取值范围．
20．（山东卷21）
已知函数
其中
为常数.
（Ⅰ）当
时，求函数
的极值；
（Ⅱ）当
时，证明：对任意的正整数
,当
时，有
.
复习题（三）答案
三、填空题
1．（江西卷1）在复平面内，复数对应的点位于第 象限四
2．（山东卷2）设z的共轭复数是，或z+=4,z·＝8，则等于 ±i
3.（福建卷4)函数,若,则的值为 0
4．集合，则
分析：
，
，又
∴ 
5．(山东文)给出命题：若函数是幂函数，则函数的图象不过第四象限．在它的逆命题、否命题、逆否命题三个命题中，真命题的个数是 1
6.（重庆卷13)已知(a>0) ，则 .3
7．（广东卷7）设，若函数，有大于零的极值点，则的取值范围是
8．（广东卷12）已知函数，，则的最小正周期是
．
9．（全国一9）设奇函数在上为增函数，且，则不等式的解集为
10.（四川卷11）设定义在上的函数满足，若，则 
11．（全国二8）若动直线与函数和的图像分别交于两点，则的最大值为
12．（四川卷10）设，其中，则是为偶函数的
条件。充要
13．（上海卷11）方程的解可视为函数的图像与函的图像交点的横坐标，若的各个实根所对应的点均在直线的同侧，则实数的取值范围是
(－∞, －6)∪(6,+∞)
14．（天津卷10）设，若对于任意的，都有满足方程，这时的取值集合为
四、解答题
15．已知集合
，集合 。
（1）若，求实数的取值范围；
（2）若，求实数的取值范围。
（１）
（２）
16．（山东卷17）
已知函数f(x)＝为偶函数，且函数图象的两相邻对称轴间的距离为
（Ⅰ）求的值；
（Ⅱ）将函数的图象向右平移个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数的图象，求的单调递减区间.
解：（Ⅰ）
＝
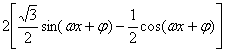
＝2sin(
-)
因为
为偶函数，所以对
恒成立，
因此 sin（--）＝sin(-).即
-sin
cos(
-)+cossin(-)=sincos(-)+cossin(-),
整理得 sincos(-)=0.因为 
＞0，且x∈R,所以 cos（-）＝0.
又因为 0＜＜π，故 -＝
.所以 f(x)＝2sin(+)=2cos.
由题意得 
故 f(x)=2cos2x.
因为 
（Ⅱ）将f(x)的图象向右平移个
个单位后，得到
的图象，再将所得图象横坐标伸长到原来的4倍，纵坐标不变，得到
的图象.
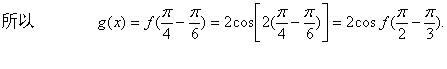
当 2kπ≤
≤2
kπ+ π (k∈Z),
即 4kπ＋≤
≤x≤4kπ+
(k∈Z)时，g(x)单调递减.
因此g(x)的单调递减区间为 
(k∈Z)
17．已知定义域为R的函数是奇函数，若对任意的tÎR，不等式恒成立，（1）求的值；（2）求的取值范围。
解：（Ⅰ）因为f（x）是定义在R上的奇函数，所以f（0）＝0，即
，解得b＝1，
从而有
．又由
知
，解得a＝2．
（Ⅱ）由（Ⅰ）知
，由上式易知f（x）在
上为减函数．由f（x）为奇函数，得：不等式
等价于
， 又f（x）为减函数，由上式推得：
，即对一切
有
，从而判别式
，解得
18．（湖北卷20）
水库的蓄水量随时间而变化，现用表示时间，以月为单位，年初为起点，根据历年数据，某水库的蓄水量（单位：亿立方米）关于的近似函数关系式为
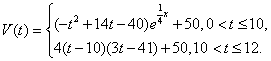
（Ⅰ）该水库的蓄求量小于50的时期称为枯水期.以表示第1月份（）,同一年内哪几个月份是枯水期？
（Ⅱ）求一年内该水库的最大蓄水量（取计算）.
解：（Ⅰ）①当0＜t
10时，V(t)=(-t2+14t-40)
化简得t2-14t+40>0,
解得t＜4，或t＞10，又0＜t10，故0＜t＜4.
②当10＜t12时，V（t）＝4（t-10）（3t-41）+50＜50,
化简得（t-10）（3t-41）＜0,
解得10＜t＜
，又10＜t12,故 10＜t12.
综合得0<t<4,或10<t12,
故知枯水期为1月，2月，，3月，4月，11月，12月共6个月.
(Ⅱ)(Ⅰ)知：V(t)的最大值只能在（4，10）内达到.
由V′（t）=
令V′(t)=0,解得t=8(t=-2舍去).
当t变化时，V′(t) 与V (t)的变化情况如下表：
| t | (4,8) | 8 | (8,10) |
| V′(t) | + | 0 | - |
| V(t) |
| 极大值 |
|
由上表，V(t)在t＝8时取得最大值V(8)＝8e2+50-108.52(亿立方米).
故知一年内该水库的最大蓄水量是108.32亿立方米
19．已知函数（），其中．
（Ⅰ）当时，讨论函数的单调性；
（Ⅱ）若函数仅在处有极值，求的取值范围；
（Ⅲ）若对于任意的，不等式在上恒成立，求的取值范围．
本小题主要考查利用导数研究函数的单调性、函数的最大值、解不等式等基础知识，考查综合分析和解决问题的能力．满分14分．
（Ⅰ）解：
．
当时，
．
令
，解得
，
，
．
当
变化时，
，的变化情况如下表：
|
|
| 0 |
|
|
| 2 |
|
|
| － | 0 | ＋ | 0 | － | 0 | ＋ |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以在
，
内是增函数，在
，
内是减函数．
（Ⅱ）解：
，显然不是方程
的根．
为使仅在处有极值，必须
成立，即有
．
解些不等式，得
．这时，
是唯一极值．
因此满足条件的的取值范围是
．
（Ⅲ）解：由条件，可知
，从而
恒成立．
当
时，
；当
时，
．
因此函数在上的最大值是
与
两者中的较大者．
为使对任意的，不等式
在上恒成立，当且仅当
，即
，在上恒成立．
所以
，因此满足条件的的取值范围是
．
20．（山东卷21）（本小题满分12分）
已知函数其中n∈N*,a为常数.
（Ⅰ）当n=2时，求函数f(x)的极值；
（Ⅱ）当a=1时，证明：对任意的正整数n,当x≥2时，有f(x)≤x-1.
解：（Ⅰ）由已知得函数f(x)的定义域为{xx＞1}，
当n=2时，
所以 
（1）当a＞0时，由f(x)=0得
＞1，
＜1，
此时 f′（x）=
.
当x∈（1，x1）时，f′（x）＜0,f(x)单调递减；
当x∈（x1+∞）时，f′（x）＞0, f(x)单调递增.
（2）当a≤0时，f′（x）＜0恒成立，所以f(x)无极值.
综上所述，n=2时，
当a＞0时，f(x)在
处取得极小值，极小值为
当a≤0时，f(x)无极值.
（Ⅱ）证法一：因为a=1,所以
当n为偶数时，
令
则 g′（x）=1+
＞0（x≥2）.
所以当x∈[2,+∞]时，g(x)单调递增，
又 g(2)=0
因此
≥g(2)=0恒成立，
所以f(x)≤x-1成立.
当n为奇数时，
要证≤x-1,由于
＜0，所以只需证ln(x-1) ≤x-1,
令 h(x)=x-1-ln(x-1),
则 h′（x）=1-
≥0（x≥2）,
所以 当x∈[2，+∞]时，
单调递增，又h(2)=1＞0，
所以当x≥2时，恒有h(x) ＞0,即ln（x-1）＜x-1命题成立.
综上所述，结论成立.
证法二：当a=1时，
当x≤2，时，对任意的正整数n，恒有≤1，
故只需证明1+ln(x-1) ≤x-1.
令
则
当x≥2时，
≥0，故h(x)在
上单调递增，
因此 当x≥2时，h(x)≥h(2)=0，即1+ln(x-1) ≤x-1成立.
故 当x≥2时，有
≤x-1.
即f（x）≤x-1