高二数学下学期期末复习题(四) 08年07月
班级 学号 得分
一、填空题
1.不等式![]() 的解集是_____________.
的解集是_____________.
2.若方程![]() 在区间(1,2]上有且仅有一个根,则实数a的取值范围是_____.
在区间(1,2]上有且仅有一个根,则实数a的取值范围是_____.
3.国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800 元而不超过4000
元的按超过800元部分的14%纳税;超过4000元的按全部稿酬的11%纳税.已知某人出
版一本书,共纳税420元时,这个人应得稿费(扣税前)为 元.
4.已知函数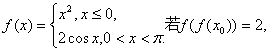 则x0=
.
则x0=
.
5.若对于任意a![]() [-1,1], 函数f(x) = x
[-1,1], 函数f(x) = x![]() + (a-4)x + 4-
+ (a-4)x + 4-
围是 .
6.如果函数f(x)的定义域为R,对于![]()
是不大于5的正整数,当x>-1时,f(x)>0. 那么具有这种性质的函数f(x)= .(注:
填上你认为正确的一个函数即可)
7.集合A、B各有2个元素,![]() 中有一个元素,若集合C同时满足①
中有一个元素,若集合C同时满足①![]() ,②
,②![]() ,则满足条件的集合C的个数是________.
,则满足条件的集合C的个数是________.
8. 若函数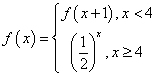 ,则
,则![]() =________.
=________.
9. 函数![]() 的定义域为[
的定义域为[![]() ],值域为[0,2],则
],值域为[0,2],则![]() 的最小值是________.
的最小值是________.
10. 一个由9辆轿车组成的车队,要通过一个长为8![]() 的隧道,若轿车的速度为
的隧道,若轿车的速度为![]()
![]() ,为了安全,两辆轿车的间距不得小于
,为了安全,两辆轿车的间距不得小于![]() (每辆轿车的长度忽略不计),那么车队全部通过隧道,至少需要_________分钟.
(每辆轿车的长度忽略不计),那么车队全部通过隧道,至少需要_________分钟.
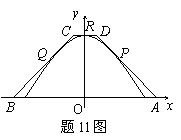
11. 如图,等腰梯形![]() 的三边
的三边![]() 分别与函数
分别与函数![]() ,
,![]() 的图象切于点
的图象切于点![]() ,则梯形
,则梯形![]() 面积的最小值是_________.
面积的最小值是_________.
 | |||
 | |||
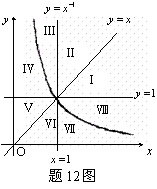
12. 幂函数![]() ,
,![]() 及直线
及直线![]() ,④
,④![]() 将直角坐标系第一象限分成八个“卦限”:Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ(如图所示),那么幂函数
将直角坐标系第一象限分成八个“卦限”:Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ,Ⅵ,Ⅶ,Ⅷ(如图所示),那么幂函数![]() 的图象在第一象限中经过的“卦限”是
的图象在第一象限中经过的“卦限”是
13.已知关于x的方程![]() 无实根,其中
无实根,其中![]() ,
,![]() 可能取的一
可能取的一
个值是
14. 函数f(x)=lg(ax-bx) (a >1>b>0),则f(x)>0的解集为(1,+∞) 的充要条件是
二、解答题
15.设f(x)=ax2+bx+c,且 f(1)=![]() ,如果不等式x2+
,如果不等式x2+![]() ≤f(x)≤2x2+2x+
≤f(x)≤2x2+2x+![]() 对一切实数x都成立.
对一切实数x都成立.
(1)求![]() ;
;
(2)求函数f(x)解析式.
16. 如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=
(I)要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(II)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
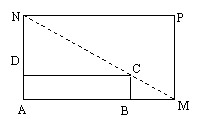 (Ⅲ)若AN的长度不少于6米,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
(Ⅲ)若AN的长度不少于6米,则当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
17.已知f(x)=xx-a+2x-3.
(I) 当a=4,2≤x≤5时,问x分别取何值时,函数f(x)取得最大值和最小值,并求出相应的最大值和最小值;
(II) 求a 的取值范围,使得f(x)在R上恒为增函数.
18. 函数f(x)=![]() (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+ f(m–x)= 4恒成立?为什么?
19.已知函数![]() ,(x>0).
,(x>0).
(I)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(II)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb]
(m≠0),求m的取值范围.
期末复习试卷
考试时间120分钟 本卷满分160分 命题人:王朝和
一、填空题(本大题共10小题,每题5分,合计50分,请将答案填入答题纸的相应位置)
1.不等式![]() 的解集是_____________.
的解集是_____________.
2.若方程![]() 在区间(1,2]上有且仅有一个根,则实数a的取值范围是_____.
在区间(1,2]上有且仅有一个根,则实数a的取值范围是_____.
3.. 13.国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800 元而不超过4000元的按超过800元部分的14%纳税;超过4000元的按全部稿酬的11%纳税.已知某人出版一本书,共纳税420元时,这个人应得稿费(扣税前)为 元.
4.已知函数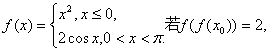 则x0=
.
则x0=
.
5.若对于任意a![]() [-1,1], 函数f(x) = x
[-1,1], 函数f(x) = x![]() + (a-4)x + 4-
+ (a-4)x + 4-
6.如果函数f(x)的定义域为R,对于![]() 是不大于5的正整数,当x>-1时,f(x)>0. 那么具有这种性质的函数f(x)= .(注:填上你认为正确的一个函数即可)
是不大于5的正整数,当x>-1时,f(x)>0. 那么具有这种性质的函数f(x)= .(注:填上你认为正确的一个函数即可)
7.. 集合A、B各有2个元素,![]() 中有一个元素,若集合C同时满足①
中有一个元素,若集合C同时满足①![]() ,②
,②![]() ,则满足条件的集合C的个数是________.
,则满足条件的集合C的个数是________.
8. 若函数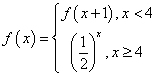 ,则
,则![]() =________.
=________.
9. 函数![]() 的定义域为[
的定义域为[![]() ],值域为[0,2],则
],值域为[0,2],则![]() 的最小值是________.
的最小值是________.
10. 一个由9辆轿车组成的车队,要通过一个长为8![]() 的隧道,若轿车的速度为
的隧道,若轿车的速度为![]()
![]() ,为了安全,两辆轿车的间距不得小于
,为了安全,两辆轿车的间距不得小于![]() (每辆轿车的长度忽略不计),那么车队全部通过隧道,至少需要_________分钟.
(每辆轿车的长度忽略不计),那么车队全部通过隧道,至少需要_________分钟.
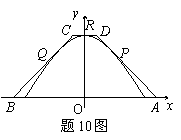 11. 如图,等腰梯形
11. 如图,等腰梯形![]() 的三边
的三边![]() 分别与函数
分别与函数![]() ,
,![]() 的图象切于点
的图象切于点![]() ,则梯形
,则梯形![]() 面积的最小值是_________.
面积的最小值是_________.
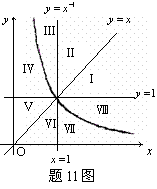 |
12. 幂函数![]() ,
,![]() 及直线
及直线![]() ,④
,④![]() 将直角
将直角
坐标系第一象限分成八个“卦限”:Ⅰ,Ⅱ,Ⅲ,Ⅳ,
Ⅴ,Ⅵ,Ⅶ,Ⅷ(如图所示),那么幂函数![]() 的
的
图象在第一象限中经过的“卦限”是
13.已知关于x的方程![]() 无实根,其中
无实根,其中![]() ,
,![]() 可能取的一个值是
可能取的一个值是
14. 函数f(x)=lg(ax-bx) (a >1>b>0),则f(x)>0的解集为(1,+∞) 的充要条件是
三、解答题(本大题共5题,合计80分,请将有关的解题过程写在答题纸的相应位置)
17.(本题14分) 设f(x)=ax2+bx+c,且 f(1)=![]() ,如果不等式x2+
,如果不等式x2+![]() ≤f(x)≤2x2+2x+
≤f(x)≤2x2+2x+![]() 对一切实数x都成立.
对一切实数x都成立.
(1)求![]() ;
;
(2)求函数f(x)解析式.
18. (本题16分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花园AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知AB=
(I)要使矩形AMPN的面积大于
(II)当AN的长度是多少时,矩形AMPN的面积最小?并求出最小面积.
 (Ⅲ)若AN的长度不少于
(Ⅲ)若AN的长度不少于
19.(本题16分) 已知f(x)=xx-a+2x-3.
(I) 当a=4,2≤x≤5时,问x分别取何值时,函数f(x)取得最大值和最小值,并求出相应的最大值和最小值;
(II) 求a 的取值范围,使得f(x)在R上恒为增函数.
20. (本题16分) 函数f(x)=![]() (a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(a,b是非零实常数),满足f(2)=1,且方程f(x)=x有且仅有一个解。
(1)求a、b的值;
(2)是否存在实常数m,使得对定义域中任意的x,f(x)+ f(m–x)= 4恒成立?为什么?
21. (本题18分) 已知函数![]() ,(x>0).
,(x>0).
(I)当0<a<b,且f(a)=f(b)时,求证:ab>1;
(II)是否存在实数a,b(a<b),使得函数y=f(x)的定义域、值域都是[a,b],若存在,则求出a,b的值,若不存在,请说明理由.
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为 [a,b]时,值域为 [ma,mb]
(m≠0),求m的取值范围.
参考答案及评分标准
一、填空题
1.![]() 2.
2.![]() 3.8 4.4 5.9 6.4 7.
3.8 4.4 5.9 6.4 7. ![]() 8.
8.![]()
9. 48 10.![]()
二、选择题
11.D 12.C 13.B 14.D 15. D 16. A
三、解答题
17. 解:(1) a+b+c=![]() ; …………………………2分
; …………………………2分
当x=-1时x2+![]() =2x2+2x+
=2x2+2x+![]() =
=![]() ,…………………………4分
,…………………………4分
所以f(-1)= ![]() …………………………………6分
…………………………………6分
(2)由(1)知a-b+c=![]() ∴c=
∴c=![]() -a,b=1
………………………………………8分
-a,b=1
………………………………………8分
∴x2+![]() ≤ax2+x+
≤ax2+x+![]() -a≤2x2+2x+
-a≤2x2+2x+![]() 恒成立, 即
恒成立, 即![]() 恒成立……10分
恒成立……10分
从而有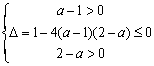 ,………………………12分
,………………………12分
∴a=![]() ∴存在f(x)=
∴存在f(x)= ![]() x2+x+1满足条件. ………………………14分
x2+x+1满足条件. ………………………14分
18. 解:设AN的长为x米(x >2), ∵![]() ,∴AM=
,∴AM=![]() ……2分
……2分
∴SAMPN=AN•AM=![]()
(I)由SAMPN > 32 得
![]() > 32 ,……………………………4分
> 32 ,……………………………4分
∵x >2,∴![]() ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴![]() ,即AN长的取值范围是
,即AN长的取值范围是![]() ………6分
………6分
(II)![]()
![]() ……………………………8分
……………………………8分
当且仅当![]() ,y=
,y=![]() 取得最小值.
取得最小值.
即SAMPN取得最小值24(平方米)…………………………………10分
(Ⅲ)令y=![]() ,则y′=
,则y′=![]() …………12分
…………12分
∴当x > 4,y′> 0,即函数y=![]() 在(4,+∞)上单调递增,
在(4,+∞)上单调递增,
∴函数y=![]() 在[6,+∞]上也单调递增……………………………14分
在[6,+∞]上也单调递增……………………………14分
∴当x=6时y=![]() 取得最小值,即SAMPN取得最小值27(平方米).………16分
取得最小值,即SAMPN取得最小值27(平方米).………16分
注:对于第(Ⅲ)问学生直接利用对勾函数单调性,而没有加以证明的,得2分.
19. 解:(Ⅰ)当![]() 时,
时,![]()
(1)![]() 时,
时,![]() ………2分
………2分
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() …………4分
…………4分
(2)当![]() 时,
时,![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() …………6分
…………6分
综上所述,当![]() 或4时,
或4时,![]() ;当
;当![]() 时,
时,![]() ……8分
……8分
(Ⅱ)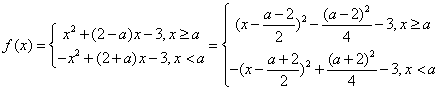 …12分
…12分
![]() 在
在![]() 上恒为增函数的充要条件是
上恒为增函数的充要条件是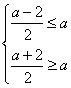 ,……………………14分
,……………………14分
解得![]()
即当![]() 时,
时,![]() 在
在![]() 上恒为增函数……………………………16分
上恒为增函数……………………………16分
20. 解(1)由f(2)=1得![]() =x的解,
=x的解,
所以![]() =1无解或有解为0,………………………………4分
=1无解或有解为0,………………………………4分
若无解,则ax+b=1无解,得a=0,矛盾;
若有解为0,则b=1,所以a=![]() . …………………………8分
. …………………………8分
(2)f(x)=![]() ,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
,设存在常数m,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,
取x=0,则f(0)+f(m–0)=4,即![]() =4,m= –4(必要性),………………12分
=4,m= –4(必要性),………………12分
又m= –4时,f(x)+f(–4–x)=![]() =……=4成立(充分性) ,
=……=4成立(充分性) ,
所以存在常数m= –4,使得对定义域中任意的x,f(x)+f(m–x)=4恒成立,………16分
21.解:(I) ∵x>0,∴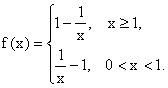
∴f(x)在(0,1)上为减函数,在![]() 上是增函数.
上是增函数.
由0<a<b,且f(a)=f(b),可得 0<a![]() 1<b和
1<b和![]() .
.
即![]() .∴2ab=a+b>
.∴2ab=a+b>![]() .……………………………………3分
.……………………………………3分
故![]() ,即ab>1.……………………………………4分
,即ab>1.……………………………………4分
(II)不存在满足条件的实数a,b.
若存在满足条件的实数a,b,使得函数y=![]() 的定义域、值域都是[a,b],
的定义域、值域都是[a,b],
则a>0. 而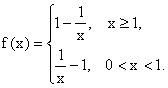
①当![]() 时,
时,![]() 在(0,1)上为减函数.
在(0,1)上为减函数.
故![]() 即
即 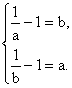 解得 a=b.
解得 a=b.
故此时不存在适合条件的实数a,b.………………………………6分
②当![]() 时,
时,![]() 在
在![]() 上是增函数.
上是增函数.
故![]() 即
即 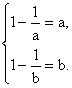
此时a,b是方程![]() 的根,此方程无实根.
的根,此方程无实根.
故此时不存在适合条件的实数a,b.………………………………8分
③当![]() ,
,![]() 时,由于
时,由于![]() ,而
,而![]() ,
,
故此时不存在适合条件的实数a,b.
综上可知,不存在适合条件的实数a,b.………………………………10分
(III)若存在实数a,b(a<b),使得函数y=f(x)的定义域为[a,b]时,值域为[ma,mb].
则a>0,m>0.
①
当![]() 时,由于f(x)在(0,1)上是减函数,故
时,由于f(x)在(0,1)上是减函数,故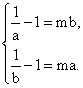 .此时刻得a,b异号,不符合题意,所以a,b不存在.
………………………………12分
.此时刻得a,b异号,不符合题意,所以a,b不存在.
………………………………12分
②
当![]() ,
,![]() 时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
时,由(II)知0在值域内,值域不可能是[ma,mb],所以a,b不存在.
故只有![]() .………………………………14分
.………………………………14分
∵![]() 在
在![]() 上是增函数,
上是增函数,
∴![]() 即
即 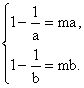 所以b是方程
所以b是方程![]() 的两个根.
的两个根.
即关于x的方程![]() 有两个大于1的实根.……………………16分
有两个大于1的实根.……………………16分
设这两个根为![]() ,
,![]() .则
.则![]() +
+![]() =
=![]() ,
,![]() ·
·![]() =
=![]() .
.
∴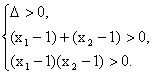 即
即 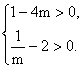 解得
解得 ![]() .
.
故m的取值范围是![]() .…………………………………………18分
.…………………………………………18分