典型例题一
例1 已知![]() ,求证
,求证![]()
证明:∵ ![]() ,
,
![]() ,
,
![]() , 三式相加,得
, 三式相加,得
![]() ,即
,即![]()
说明:这是一个重要的不等式,要熟练掌握.
典型例题二
例2 已知![]() 是互不相等的正数,
是互不相等的正数,
求证:![]()
证明:∵![]() ,
,
∴![]()
同理可得:![]() .
.
三个同向不等式相加,得
![]() ①
①
说明:此题中![]() 互不相等,故应用基本不等式时,等号不成立.特别地,
互不相等,故应用基本不等式时,等号不成立.特别地,![]() ,
,![]() 时,所得不等式①仍不取等号.
时,所得不等式①仍不取等号.
典型例题三
例3 求证![]() .
.
分析:此问题的关键是“灵活运用重要基本不等式![]() ,并能由
,并能由![]() 这一特征,思索如何将
这一特征,思索如何将![]() 进行变形,进行创造”.
进行变形,进行创造”.
证明:∵![]() ,
,
两边同加![]() 得
得![]() .
.
即![]() .
.
∴![]() .
.
同理可得:![]() ,
,
![]() .
.
三式相加即得![]() .
.
典型例题四
例4 若正数![]() 、
、![]() 满足
满足![]() ,则
,则![]() 的取值范围是 .
的取值范围是 .
解:∵![]() , ∴
, ∴![]() ,令
,令![]() ,得
,得![]() ,
,
∴![]() ,或
,或![]() (舍去).
(舍去).
∴![]() ,∴
,∴ ![]() 的取值范围是
的取值范围是![]()
说明:本题的常见错误有二.一是没有舍去![]() ;二是忘了还原,得出
;二是忘了还原,得出![]() .前者和后者的问题根源都是对
.前者和后者的问题根源都是对![]() 的理解,前者忽视了
的理解,前者忽视了![]() 后者错误地将
后者错误地将![]() 视为
视为![]() .
.
因此,解题过程中若用换元法,一定要对所设“元”的取值范围有所了解,并注意还原之.
典型例题五
例5 (1)求![]() 的最大值.
的最大值.
(2)求函数![]() 的最小值,并求出取得最小值时的
的最小值,并求出取得最小值时的![]() 值.
值.
(3)若![]() ,且
,且![]() ,求
,求![]() 的最小值.
的最小值.
解:(1)![]()
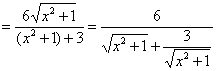
![]()
即![]() 的最大值为
的最大值为![]()
当且仅当![]() 时,即
时,即![]()
![]() 时,取得此最大值.
时,取得此最大值.
(2)![]()
![]()
∴ ![]() 的最小值为3,当且仅当
的最小值为3,当且仅当![]() ,即
,即![]() ,
,![]() ,
,![]() 时取得此最小值.
时取得此最小值.
(3)∴ ![]() ∴
∴![]() 即
即![]()
∵![]() ∴
∴![]() 即
即![]() 的最小值为2.
的最小值为2.
当且仅当![]() 时取得此最小值.
时取得此最小值.
说明:解这类最值,要选好常用不等式,特别注意等号成立的条件.
典型例题六
例6 求函数![]() 的最值.
的最值.
分析:本例的各小题都可用最值定理求函数的最值,但是应注意满足相应条件.如:![]() ,应分别对
,应分别对![]() 两种情况讨论,如果忽视
两种情况讨论,如果忽视![]() 的条件,就会发生如下错误:∵
的条件,就会发生如下错误:∵ ![]() ,
,![]()
解:当![]() 时,
时,![]() ,又
,又![]() ,
,
当且仅当![]() ,即
,即![]() 时,函数
时,函数![]() 有最小值
有最小值![]()
∴ ![]()
当![]() 时,
时,![]() ,又
,又![]() ,
,
当且仅当![]() ,即
,即![]() 时,函数
时,函数![]() 最小值
最小值![]()
∴ ![]()
典型例题七
例7 求函数![]() 的最值.
的最值.
分析:![]() .
.
但等号成立时![]() ,这是矛盾的!于是我们运用函数
,这是矛盾的!于是我们运用函数![]() 在
在![]() 时单调递增这一性质,求函数
时单调递增这一性质,求函数![]() 的最值.
的最值.
解:设![]() ,
,
∴![]() .
.
当![]() 时,函数
时,函数![]() 递增.
递增.
故原函数的最小值为![]() ,无最大值.
,无最大值.
典型例题八
例8 求函数![]() 的最小值.
的最小值.
分析:用换元法,设![]() ,原函数变形为
,原函数变形为![]() ,再利用函数
,再利用函数![]() 的单调性可得结果.或用函数方程思想求解.
的单调性可得结果.或用函数方程思想求解.
解:解法一:
设![]() ,故
,故![]()
![]() .
.
由![]() ,得:
,得:![]() ,故:
,故:![]() .
.
∴函数![]() 为增函数,从而
为增函数,从而![]() .
.
解法二:
设![]() ,知
,知![]() ,可得关于
,可得关于![]() 的二次方程
的二次方程![]() ,由根与系数的关系,得:
,由根与系数的关系,得:![]() .
.
又![]() ,故有一个根大于或等于2,
,故有一个根大于或等于2,
设函数![]() ,则
,则![]() ,即
,即![]() ,故
,故![]() .
.
说明:本题易出现如下错解:![]() .要知道,
.要知道,![]() 无实数解,即
无实数解,即![]() ,所以原函数的最小值不是2.错误原因是忽视了等号成立的条件.
,所以原函数的最小值不是2.错误原因是忽视了等号成立的条件.
当![]() 、
、![]() 为常数,且
为常数,且![]() 为定值,
为定值,![]() 时,
时,![]() ,不能直接求最大(小)值,可以利用恒等变形
,不能直接求最大(小)值,可以利用恒等变形![]() ,当
,当![]() 之差最小时,再求原函数的最大(小)值.
之差最小时,再求原函数的最大(小)值.
典型例题九
例9 ![]() 求
求![]() 的最小值.
的最小值.
分析:此题出现加的形式和平方,考虑利用重要不等式求最小值.
解:由![]() ,得
,得![]()
又![]() 得
得![]() ,即
,即![]() .
.
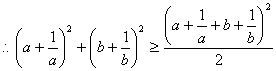
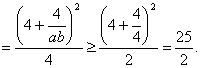
故![]() 的最小值是
的最小值是![]() .
.
说明:本题易出现如下错解:
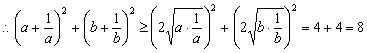 ,故
,故![]() 的最小值是8.
的最小值是8.
错误的原因是,在两次用到重要不等式当等号成立时,有![]() 和
和![]() ,但在
,但在![]() 的条件下,这两个式子不会同时取等号(
的条件下,这两个式子不会同时取等号(![]() ).排除错误的办法是看都取等号时,与题设是否有矛盾.
).排除错误的办法是看都取等号时,与题设是否有矛盾.
典型例题十
例10 已知:![]() ,求证:
,求证:![]() .
.
分析:根据题设,可想到利用重要不等式进行证明.
证明:![]()
同理:![]()
![]()
![]()
说明:证明本题易出现的思维障碍是:(1)想利用三元重要不等式解决问题;(2)不会利用重要不等式![]() 的变式;(3)不熟练证明轮换对称不等式的常用方法.因此,在证明不等式时,应根据求证式两边的结构,合理地选择重要不等式.另外,本题的证明方法在证轮换对称不等式时具有一定的普遍性.
的变式;(3)不熟练证明轮换对称不等式的常用方法.因此,在证明不等式时,应根据求证式两边的结构,合理地选择重要不等式.另外,本题的证明方法在证轮换对称不等式时具有一定的普遍性.
典型例题十一
例11设![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
分析:如何将![]() 与
与![]() 用不等式的形式联系起来,是本题获解的关键.算术平均数与几何平均数定理
用不等式的形式联系起来,是本题获解的关键.算术平均数与几何平均数定理![]() 两边同加
两边同加![]() 之后得
之后得![]() .
.
解:由![]() ,则有
,则有
![]()
![]()
![]()
说明:常有以下错解:
![]() ,
,
![]() .
.
故![]() .
.
两式相除且开方得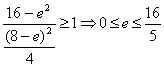 .
.
错因是两不等式相除,如![]() ,相除则有
,相除则有![]() .
.
不等式![]() 是解决从“和”到“积”的形式.从“和”到“积”怎么办呢?有以下变形:
是解决从“和”到“积”的形式.从“和”到“积”怎么办呢?有以下变形:![]() 或
或![]() .
.
典型例题十二
例12 已知:![]() ,且:
,且:![]() ,求证:
,求证:![]() ,并且求等号成立的条件.
,并且求等号成立的条件.
分析:由已知条件![]() ,可以考虑使用均值不等式,但所求证的式子中有
,可以考虑使用均值不等式,但所求证的式子中有![]() ,无法利用
,无法利用![]() ,故猜想先将所求证的式子进行变形,看能否出现
,故猜想先将所求证的式子进行变形,看能否出现![]() 型,再行论证.
型,再行论证.
证明:![]()
![]()
![]()
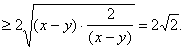
等号成立,当且仅当![]() 时.
时.
![]()
![]()
![]()
由以上得![]()
即当![]() 时等号成立.
时等号成立.
说明:本题是基本题型的变形题.在基本题型中,大量的是整式中直接使用的均值不等式,这容易形成思维定式.本题中是利用条件将所求证的式子化成分式后再使用均值不等式.要注意灵活运用均值不等式.
典型例题十三
例13 已知![]() ,且
,且![]() ,求
,求![]() 的最大值.
的最大值.
分析:由![]() ,可得,
,可得,![]()
故![]() ,令
,令![]() .
.
利用判别式法可求得![]() (即
(即![]() )的最大值,但因为
)的最大值,但因为![]() 有范围
有范围![]() 的限制,还必须综合韦达定理展开讨论.仅用判别式是不够的,因而有一定的麻烦,下面转用基本不等式求解.
的限制,还必须综合韦达定理展开讨论.仅用判别式是不够的,因而有一定的麻烦,下面转用基本不等式求解.
解法一:由![]() ,可得,
,可得,![]() .
.
![]()
![]()
注意到![]() .
.
可得,![]() .
.
当且仅当![]() ,即
,即![]() 时等号成立,代入
时等号成立,代入![]() 中得
中得![]() ,故
,故![]() 的最大值为18.
的最大值为18.
解法二:![]() ,
,![]() ,
,
代入![]() 中得:
中得:![]()
解此不等式得![]() .下面解法见解法一,下略.
.下面解法见解法一,下略.
说明:解法一的变形是具有通用效能的方法,值得注意:而解法二则是抓住了问题的本质,所以解得更为简捷.
典型例题十四
例14 若![]() ,且
,且![]() ,求证:
,求证:![]() .
.
分析:不等式右边的数字“8”使我们联想到可能是左边三个因式分别使用基本不等式所得三个“2”连乘而来,而![]() .
.
证明:![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.
同理![]() ,
,![]() ,
,
![]() .
.
当且仅当![]() 时,等号成立.
时,等号成立.
说明:本题巧妙利用![]() 的条件,同时要注意此不等式是关于
的条件,同时要注意此不等式是关于![]() 的轮换式.
的轮换式.
典型例题十五
例15 设![]() ,求证:
,求证:![]() .
.
分析:本题的难点在于![]() 不易处理,如能找出
不易处理,如能找出![]() 与
与![]() 之间的关系,问题可得到解决,注意到:
之间的关系,问题可得到解决,注意到:
![]() ,
,
则容易得到证明.
证明:![]() ,
,
于是![]()
同理:![]() ,
,![]() .
.
三式相加即得:![]() .
.
说明:注意观察所给不等式的结构,此不等式是关于![]() 的轮换式.因此只需抓住一个根号进行研究,其余同理可得,然后利用同向不等式的可加性.
的轮换式.因此只需抓住一个根号进行研究,其余同理可得,然后利用同向不等式的可加性.
典型例题十六
例16 已知:![]() (其中
(其中![]() 表示正实数)
表示正实数)
求证: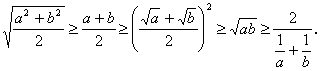
分析:要证明的这一串不等式非常重要,![]() 称为平方根,
称为平方根,![]() 称为算术平均数,
称为算术平均数,![]() 称为几何平均数,
称为几何平均数,![]() 称为调和平均数.
称为调和平均数.
证明: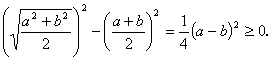
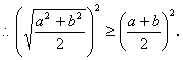
![]()
∴![]() ,当且仅当“
,当且仅当“![]() ”时等号成立.
”时等号成立.
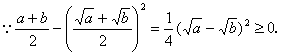
∴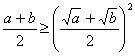 ,等号成立条件是“
,等号成立条件是“![]() ”
”
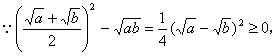
∴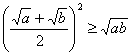 ,等号成立条件是“
,等号成立条件是“![]() ”.
”.
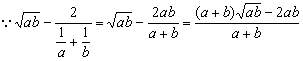
![]()
∴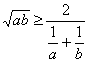 ,等号成立条件是“
,等号成立条件是“![]() ”.
”.
说明:本题可以作为均值不等式推论,熟记以上结论有利于处理某些复杂不等式的证明问题.本例证明过程说明,不等式性质中的比较法是证明不等式的最基本、最重要的方法.
典型例题十七
例17 设实数![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() ,求证
,求证![]() .
.
分析:由条件可得到![]() ,
,![]() ,
,![]() ,
, ![]() 同号.为方便,不妨都设为正.将求证式子的左边展开后可看出有交叉项
同号.为方便,不妨都设为正.将求证式子的左边展开后可看出有交叉项![]() 和
和![]() 无法利用条件,但使用均值不等式变成乘积后,重新搭配,可利用条件求证.
无法利用条件,但使用均值不等式变成乘积后,重新搭配,可利用条件求证.
证明:![]()
同理,由![]() 知
知![]() 与
与![]() 同号,
同号,![]() 与
与![]() 同号
同号
∴![]() ,
,![]() ,
,![]() ,
,![]() 同号.不妨都设为正.
同号.不妨都设为正.
![]()
![]()
![]()
![]()
![]()
![]() ,
,
即![]() .
.
说明:本题是根据题意分析得![]() ,
,![]() ,
,![]() ,
,![]() 同号,然后利用均值不等式变形得证.换一个角度,由条件的特点我们还会联想到使用二次方程根的判别式,可能会有另一类证法.
同号,然后利用均值不等式变形得证.换一个角度,由条件的特点我们还会联想到使用二次方程根的判别式,可能会有另一类证法.
实际上,由条件可知![]() ,
,![]() ,
,![]() ,
,![]() 为同号,不妨设同为正.又∵
为同号,不妨设同为正.又∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() .
.
不等式![]() ,
,![]() 对任意实数
对任意实数![]() 恒成立(根据二次三项式恒为正的充要条件),两式相加得
恒成立(根据二次三项式恒为正的充要条件),两式相加得![]() ,它对任意实数
,它对任意实数![]() 恒成立.同上可得:
恒成立.同上可得:![]() .
.
典型例题十八
例18 如下图所示,某畜牧基地要围成相同面积的羊圈4间,一面可利用原有的墙壁,其余各面用篱笆围成,篱笆总长为36m.问每间羊圈的长和宽各为多少时,羊圈面积最大?
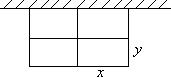
分析:可先设出羊圈的长和宽分别为![]() ,
,![]() ,即求
,即求![]() 的最大值.注意条件
的最大值.注意条件![]() 的利用.
的利用.
解:设每间羊圈的长、宽分别为![]() ,
,![]() ,则有
,则有![]() ,即
,即![]() .设
.设![]()
![]()
![]()
上式当且仅当![]() 时取“=”.
时取“=”.
此时![]()
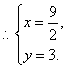
∴羊圈长、宽分别为![]() m,3m时面积最大.
m,3m时面积最大.
说明:(1)首先应设出变量(此处是长和宽),将题中条件数学化(即建立数学模型)才能利用数学知识求解;(2)注意在条件![]() 之下求积
之下求积![]() 的最大值的方法:直接用不等式
的最大值的方法:直接用不等式![]() ,即可出现积
,即可出现积![]() .当然,也可用“减少变量”的方法:
.当然,也可用“减少变量”的方法:![]() ,当且仅当
,当且仅当![]() 时取“=”.
时取“=”.
典型例题十九
例19 某单位建造一间地面面积为12m2的背面靠墙的矩形小房,房屋正面的造价为1200元/m2,房屋侧面的造价为800 元/m2,屋顶的造价为5800元.如果墙高为3m,且不计房屋背面的费用,问怎样设计房屋能使总造价最低,最低总造价是多少元?
分析:这是一个求函数最小值的问题,关键的问题是设未知数,建立函数关系.从已知条件看,矩形地面面积为12m2,但长和宽不知道,故考虑设宽为![]() m,则长为
m,则长为![]() m,再设总造价为
m,再设总造价为![]() .由题意就可以建立函数关系了.
.由题意就可以建立函数关系了.
解:设矩形地面的正面宽为![]() m,则长为
m,则长为![]() m;设房屋的总造价为
m;设房屋的总造价为![]() .根据题意,可得:
.根据题意,可得:
![]()
![]()
![]()
![]()
当![]() ,即
,即![]() 时,
时,![]() 有最小值34600元.
有最小值34600元.
因此,当矩形地面宽为4m时,房屋的总造价最低,最低总造价是34600元.
说明:本题是函数最小值的应用题,这类题在我们的日常生活中经常遇到,有求最小值的问题,也有求最大值的问题,这类题都是利用函数式搭桥,用均值不等式解决,解决的关键是等号是否成立,因此,在解这类题时,要注意验证等号的成立.
典型例题二十
例20 某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每1m长造价40元,两侧墙砌砖,每1m长造价45元,顶部每1m2造价20元.计算:
(1)仓库底面积S的最大允许值是多少?
(2)为使S达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?
分析:用字母分别表示铁栅长和一堵砖墙长,再由题意翻译数量关系.
解:设铁栅长为![]() m,一堵砖墙长为
m,一堵砖墙长为![]() m,则有
m,则有![]() .
.
由题意得![]()
应用算术平均数与几何平均数定理,得
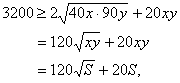
![]()
即:![]()
![]()
从而:![]()
因此![]() 的最大允许值是
的最大允许值是![]() ,取得此最大值的条件是
,取得此最大值的条件是![]() ,而
,而![]() ,由此求得
,由此求得![]() ,即铁栅的长应是
,即铁栅的长应是![]() .
.
说明:本题也可将![]() 代入(*)式,导出关于
代入(*)式,导出关于![]() 的二次方程,利用判别式法求解.
的二次方程,利用判别式法求解.
典型例题二十一
例21 甲、乙两地相距![]() ,汽车从甲地匀速行驶到乙地,速度不超过
,汽车从甲地匀速行驶到乙地,速度不超过![]() ,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
,已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() 的平方成正比,且比例系数为
的平方成正比,且比例系数为![]() ;固定部分为
;固定部分为![]() 元.
元.
(1)把全程运输成本![]() 元表示为速度
元表示为速度![]() 的函数,并指出这个函数的定义域;
的函数,并指出这个函数的定义域;
(2)为了使全程运输成本最小,汽车应以多大速度行驶?
分析:这是1997年的全国高考试题,主要考查建立函数关系式、不等式性质(公式)的应用.也是综合应用数学知识、思想和方法解决实际问题的一道优秀试题.
解:(1)依题意知汽车从甲地匀速行驶到乙地所用的时间为![]() ,全程运输成本为
,全程运输成本为
![]() .
.
故所求函数为![]() ,定义域为
,定义域为![]() .
.
(2)由于![]() 都为正数,
都为正数,
故有![]() ,
,
即![]() .
.
当且仅当![]() ,即
,即![]() 时上式中等号成立.
时上式中等号成立.
若![]() 时,则
时,则![]() 时,全程运输成本
时,全程运输成本![]() 最小;
最小;
当![]() ,易证
,易证![]() ,函数
,函数![]() 单调递减,即
单调递减,即![]() 时,
时,![]() .
.
综上可知,为使全程运输成本![]() 最小,
最小,
在![]() 时,行驶速度应为
时,行驶速度应为![]() ;
;
在![]() 时,行驶速度应为
时,行驶速度应为![]() .
.