典型例题一
例1 计算：（1）
； （2）
．
分析：本题如果直接计算组合数，运算比较繁．本题应努力在式子中创造条件使用组合数的性质，第（1）题中，
，经此变形后，可继续使用组合数性质．第（2）题有两个考虑途径，一方面可以抓住项的变形
，求和；另一方面，变形
，接着
，
…，反复使用公式．
解：（1）原式
．
（2）原式
．
另一方法是：原式
．
说明：利用第（2）小题的手段，我们可以得到组合数的一个常用的结论：
．
左边
右边．
典型例题二
例2 从7名男生5名女生中，选出5人，分别求符合下列条件的选法种数有多少种？
（1）
、
必须当选；（2）、都不当选；（3）、不全当选；（4）至少有2名女生当选；（5）选出5名同学，让他们分别担任体育委员、文娱委员等5种不同工作，但体育委员由男生担任，文娱委员由女生担任．
分析：本题是组合应用题中典型的选代表问题，通过一些明确的条件对结果进行限制．问题（1）、必须当选，它们就不必再考虑，只要再选出余下的代表．问题（2）、必须不当选，实际上就是去掉这几个元素不予考虑．问题（3）、不全当选可以从正反两方面考虑．从正面考虑可以按、全不选和、选一个分类，从反面考虑可用间接法，去掉、全选的情况．问题（4）可以按女生选2人、3人…进行分类，当然也可以从反面考虑用间接法．问题（5）可以先处理特殊位置的体育班委与文娱班委．
解：（1）除、选出外，从其它10个人中再选3人，共有的选法种数为
，
（种）．
（2）去掉、，从其它10人中任选5人，共有的选法种数为：
（种）．
（3）按、的选取情况进行分类：、全不选的方法数为
，、选1人的方法数为
，共有选法
（种）．
本小题的另一解法：从12人中选5人的选法中去掉、全选的情况，所有选法只有
（种）．
方法一：按女同学的选取情况分类：
选2名女同学、3名男同学；选3名女同学2名男同学；选4名女同学1名男同学；选5名女同学．所有选法数为：
（种）．
方法二：从反面考虑，用间接方法，去掉女同学不选或选1人的情况，所有方法总数为：
（种）．
（5）选出一个男生担任体育班委，再选出1名女生担任文娱班委，剩下的10人中任取3人担任其它3个班委．用分步计数原理可得到所有方法总数为：
（种）．
说明：对于本题第（4）小题，“至少有2名女生当选”，我们可能还有另外一种考虑，先从5名女生中选出2人，然后在剩下的10人中任选3人，得到的方法数为
（种），与上述答案比较，结果明显增多了，为什么会出现以上情况？上述步骤得到的选取结果虽然符合了有2名女生的要求，但在计数时出现了重复，比如先选两女生为
、
，剩下的10人中如果又选出了女生
，与先选两名女生为、后又选出了女生，出现了同样的结果，因为选取问题仅考虑选出了哪些元素，至于先选后选并不考虑．这里需要我们引起注意的是以后遇到“至少”类型的问题，一般采用分类法或间接法解决，在选取问题中尽可能避免出现重复计数，我们还可以进一步从下一个例子加深理解．
典型例题三
例3 空间10个点，其中有5点在同一个平面内，其余无三点共线，四点共面，问以这些点为顶点，共可构成多少个四面体？
分析：本题如果从正面考虑可以按5个共面的点的选用情况进行分类．如果从反面考虑用间接法，只要去掉从5个共面的点中任取四个点的情况，因为共面的四个点不能构成四面体的四个顶点．
解：方法一：可以按共面的点取0个、1个、2个、3个进行分类，得到所有的取法总数为：
个．
方法二：从10个点中任取4个点的方法数中去掉4个点全部取自共面的5个点的情况，得到所有构成四面体的方法数为：
（个）．
说明：以几何为背景的此类应用题中，间接方法用得比较多，在考虑去掉不符合要求的选法时，既不能多去，也不能少去，此外有时还需去掉一些重复计数的情况．比如：四面体的顶点和各条棱的中点共10个点，任取其中的4个点，其中不共面的取法有多少种？我们可以从10个点中任取4点．共有
种取法，然后去掉下面几种情况，4个点取在四面体的同一个面上，有
种取法；四个中点连成平行四边形的情形，有3种取法，还有3点在四面体的一条棱上，另一点是其它点，不考虑已计算的四点在四面体同一面上的情况，共有6种取法．用间接法可得不同的取法共有：
（种）．
典型例题四
例4 在1，3，5，7，9中任取3个数字，在0，2，4，6，8中任取两个数字，可组成多少个不同的五位偶数．
分析：因为零不能作首位数，所以是特殊元素，因此可以根据选零不选零为分类标准。
解：第一类：五位数中不含数字零。
第一步：选出5个数字，共有
种选法．
第二步：排成偶数—先排末位数，有
种排法，再排其它四位数字，有
种排法．
∴ 
（个）
第二类：五位数中含有数字零．
第一步：选出5个数字，共有
种选法。
第二步：排顺序又可分为两小类；
（1）末位排零，有
种排列方法；
（2）末位不排零．这时本位数有
种选法，而因为零不能排在首位，所以首位有
种排法，其余3个数字则有
种排法．
∴ 
∴ 符合条件的偶数个数为
（个）
说明：本题也可以用间接法（即排除法）来解．请自行完成．
典型例题五
例5 有12名划船运动员，其中3人只会划左舷，4人只会划右舷，其余5人既会划左舷也会划右舷。现在要从这12名运动员中选出6人平均分在左、右舷划船参加比赛，有多少种不同的选法？
分析：设集合A={只会划左舷的3个人}，B={只会划右舷的4个人}，C={既会划左舷又会划右舷的5个人}
先分类，以集合A为基准，划左舷的3个人中，有以下几类情况：①A中有3人；②A中有2人；C中有1人；③A中有1人，C中有2人；④C中有3人。
第①类，划左舷的人已选定，划右舷的人可以在
中选3人，即有
种选法。因是分步问题，所以有
种选法。第②类，划左舷的人在A中选2人，有
种选法，在C中选1人，有
种选法，划右舷的在中剩下的8个人中选3人，有
种选法。因是分步问题，所以有
种选法。类似地，第③类，有
种选法。第④类有
种选法。
因为是分类，所以一共有
种选法。
解：
种
答：一共有2174种不同选法．
说明：这种比较复杂的在若干个集合中选取元素的问题，只要能运用分类思想正确对所求选法分类，又能正确地根据题目要求合理地考察步骤，就可以顺利地求得解．在分类时，要注意做到既不重复也不遗漏．
这里是以集合A为基准进行分类，也可以集合B或集合C为基准进行分类，其结果是相同的，但一般都选择元素个数较少的集合作为基准来分类，这样可以减少分类，方便运算．
典型例题六
例6 甲、乙两队各出7名队员，按事先排好的顺序出场参加围棋擂台赛，双方由1号队员出赛，负者被淘汰，胜者再与负方2号队员比赛，…，直到一方队员全被淘汰为止，另一方获胜，形成一种比赛过程，试求所有可能出现的比赛过程的种类．
分析与解：若甲队取胜，比赛结果可能是
，
，
，
，
，
，
．
只有一个过程；
共8场，乙队在前7场中胜一场，有
种不同的过程；
共9场，乙队在前8场中胜二场，有
种不同的过程；
共10场，乙队在前9场中胜三场，有种不同的过程；
………………
∴ 甲队取胜的过程种数是：
类似乙队取胜也有同样的过程种数
∴ 共有
种不同的比赛过程．
说明：一个排列与另一个排列的区别有两点，一点是元素不同，另一点是顺序不同（在元素相同时）；而一个组合与另一个组合不同点仅是元素不同，由此可知，排列是有顺序问题，组合是无顺序问题．本题是一应用问题，根据实际确定是组合问题．
典型例题七
例7 从1到9的九个数字中取三个偶数四个奇数，试问：
（1）能组成多少个没有重复数字的七位数？
（2）上述七位数中三个偶数排在一起的有几个？
（3）（1）中的七位数中，偶数排在一起、奇数也排在一起的有几个？
（4）（1）中任意两偶然都不相邻的七位数有几个？
分析与解：（l）分步完成：第一步在4个偶数中取3个，可有
种情况；第二步在5个奇数中取4个，可有
种情况；第三步3个偶数，4个奇数进行排列，可有
种情况，所以符合题意的七位数有
个．
（2）上述七位数中，三个偶数排在一起的有
个．
（3）上述七位数中，3个偶数排在一起，4个奇数也排在～起的有
个．
（4）上述七位数中，偶数都不相邻，可先把4个奇数排好，再将3个偶数分别插入5个空档，共有
个．
说明：对于有限制条件的排列问题，常可分步进行，先组合再排列，这是乘法原理的典型应用．
典型例题八
例8 6本不同的书，按照以下要求处理，各有几种分法？
（1）一堆一本，一堆两本，一堆三本；
（2）甲得一本，乙得两本，丙得三本；
（3）一人得一本，一人得二本，一人得三本；
（4）平均分给甲、乙、丙三人；
（5）平均分成三堆．
分析与解：（1）先在6本书中任取一本．作为一本一堆，有
种取法，再从余下的五本书中任取两本，作为两本一堆，有
种取法，再后从余下三本取三本作为一堆，有
种取法，故共有分法
种．
（2）由（1）知．分成三堆的方法有
种，而每种分组方法仅对应一种分配方法，故甲得一本，乙得二本，丙得三本的分法亦为种．
（3）由（1）知，分成三堆的方法有种，但每一种分组方法又有不同的分配方案，故一人得一本，一人得两本，一人得三本的分法有
（种）．
（4）3个人一个一个地来取书，甲从6本不同的书本中任取出2本的方法有
种，甲不论用哪一种方法取得2本书后，已再从余下的4本书中取书有
种方法，而甲、乙不论用哪一种方法各取2本书后，丙从余下的两本中取两本书，有
种方法，所以一共有
种方法．
（5）把6本不同的书分成三堆，每推二本与把六本不同的书分给甲、乙、丙三人，每人二本的区别在于，后者相当于把六本不同的书，平均分成三难后，再把每次分得的三堆书分给甲、乙、丙三个人．因此，设把六本不同的书，平均分成三堆的方法有
种，那么把六本不同的书分给甲、乙、丙三人每人2本的分法就应
种，由（4）知，把六本不同的书分给甲、乙、丙三人，每人2本的方法有
种．
所以
，则
（种）
说明：本问题中的每一个小题都提出了一种类型问题，搞清类型的归属对今后解题大有补益，其中
（1）属非均匀分组问题． （2）属非均匀定向分配问题．
（3）属非均匀不定向分配问题．（4）属均匀不定向分配问题．
（5）属均匀分组问题．
典型例题九
例9 有6本不同的书，分给甲、乙、丙三个人．
（1）如果每人得两本，有多少种不同的分法；
（2）如果一个人得一本，一个人得2本，一个人得3本有多少种不同的分法；
（3）如果把这6本书分成三堆，每堆两本有多少种不同分法．
分析与解：（1）假设甲先拿，则甲从6本不同的书中选取2本有
种方法，不论甲取走的是哪两本书，乙再去取书时只能有
种，此时剩下的两本书自然给丙，就只有
种方法，由乘法原理得一共有
种不同分法．
（2）先假设甲得1本，乙得2本，丙得3本则有种法，一共有
种不同的分法．
（3）把6本书分成三堆，每堆2本，与次序无关．
所以一共有
种不同分法．
说明：本题的三个问题要注意区别和联系，不要混淆．
6本书分给甲、乙、丙三人每人两本和分成3堆每堆两本是有区别的，前者虽然也属均分问题，但要甲、乙、丙三个人一个人一个人的去拿，而后者属均分问题又是无序问题，所以必须除以．一般地，
个元素中有
个元素（
）均分成m堆一定要除以
．
例如：有17个桃，分成8堆，其中一堆一个，一堆4个，另外6堆每堆都是2个，有多少种不同的分法．
一共有
种不同分法．
典型例题十
例5 (1)从
名医生中选
名，
名护士中选名，分成两队，每队
名医生名护士，到甲、乙两地巡回医疗，求安排方案有多少种？
(2)从一组共名学生中选男生人，女生人，参加三种不同的活动，要求每人参加一种且每种活动都有人参加的选法有
种，问该组学生中男、女生各有多少人？
分析：(1)可以把甲、乙两地看成两个有顺序的“空”，然后选取获和护士填好，即分步完成；也可采取先选取、分堆、再排列的办法．(2)先分堆再排列．
解法一(1)：按照
进行填入．第一步，先取名医生填入两空，有
种填法；第二步，再取名护士填入两空，每空人，有
种填法，故共有安排方案
种．
解法二(1)：第一步，选人，有
种选法；第二步，平均分成堆，有
／
种分法；第三步，将两队分别安排到甲、乙两地，有种方法，故共有安排方案：
种．
解(2)：设男生人，女生
人，则有
，
∴
，
且
．
∴
或
．
∴男生有
人，女生人或男生人，女生人．
说明：本题是排列与组合的综合题．涉及到分堆、再全排列的问题．方法呆以是选人→分堆→排列，也可以直接用分步法解．第(2)小题中在解未知数时，应注意到是正整数且范围限制，可以使用还个验证的办法验证出来．
典型例题十一
例11 四个不同的小球，全部放入编号为
的四个盒子中．
(1)随便放(可以有空盒，但球必须都放入盒中)有多少种放法？
(2)四个盒都不空的放法有多少种？
(3)恰有一个空盒的放法有多少种？
(4)恰有两个空盒的放法有多少种？
(5)甲球所放盒的编号总小于乙球所放盒的编号的放法有多少种？
分析：(1)注意合理的分类；(2)可以用前面例题中先分堆再排列的方法．
解：(1)由于可以随便放，故每个小球都有种放法，所以放法总数是
种．
(2)将四个小球全排列后放入四个盒子即可，所以放法总数是
种．
(3)由题意，必然四个小球放入三个盒子中．分三步完成：选出三个盒子；将四个小球分成三堆；将三堆小球全排列后放入三个盒子．所以放法总数是：
种．
(4)由题意，必然四个小球放入个盒子中．
解法一：分三步完成：选出两个盒子；将四个小球分成两堆；将两堆小球全排列放入两个盒子．所以放法总数是：
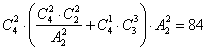种．
解法一：分两步完成：选出两个盒子；将四个球随便放入两个盒子（可以有空盒子），然后剔除四个球只放入一个盒子的情形．因此，放法总数是
种．
(5)分三类放法．
第一类：甲球放入号盒子，即
，则乙球有种放法（可放入
号盒子），其余两球可以随便放入四个盒子，有
种放法．故此类放法的种数是
；
第二类：甲球放入号盒子，即
，则乙球有种放法（可放入
号盒子），其余两球随便放，有种放法．故此类放法的种数是
；
第三类：甲球放入号盒子，即
，则乙球只有种放法（放入号盒子），其余两球随便放，有种放法．故此类放法的种数是
．
综上，所有放法的总数是：
种．
本题也可这样理解：先选出两个盒子放入甲、乙两球，有
种放法；另外两球随便放，有种放法，由乘法原理，所有放法的总数是
种．
说明：“小球放入盒子”是一种常见的、基本的数学模型，很多问题实际上都可以化归到这种模型去解决，虽然表面上看来可能相距很远。当然，小球放入盒子会有各种限制条件，应注意恰当地分类或分步．下面的例即是采用这种思想．
典型例题十二
例12 
是集合
到集合
的映射，满足
的映射有多少个？
分析：根据映射的定义，
中的每一个元素在
中都有唯一的一个像，可以把
五个元素想象成五个“小球”，把
三个元素想象成三个盒子，只要把五个小球全部放入盒子中（随便放），便可得到一个映射，因为每一个“小球”都对应着唯一的一个盒子．
解：将三个元素设想为
号盒、号盒和号盒三个盒子．只要
个元素全部放入盒子（允许有空盒）便可得到个映射．设放入号盒的元素个数为，放入号盒的元素个数为
，则放入号盒的元素个数为
个，
．则有
，
由条件
，考虑到
且，
故上述方程的解是
因此满足条件的元素的放法有三类．
第一类：放入号盒个元素，放入号盒个元素，其余元素放入号盒，放法种数是：
种．
第二类：放入号盒个元素，放入号盒个元素，其余元素放入号盒，放法种数是：
种．
第三类：全部个元素都放入号盒，放法种数为种．
所以放法总数为
种．
故符合条件的映射有
个．
说明：该题把映射问题巧妙地抽象为“小球放入盒子”问题，使问题更加形象且易于把握．事实上排列组合中的不少问题可进行类似的抽象，把一个陌生的问题转化为一个熟悉的问题去解决．另外，应注意排列组合中不定方程的整数解的解法，在中学阶段大多采用逐个验证的方法求其解．
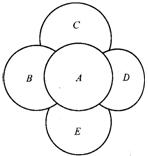
典型例题十三
例13 如图所示，、、
、
、
为个区域，现备有种颜色为个区域涂色，涂色要求：每相邻两个区域不同色，每个区域只涂一色．共有多少种不同的涂色方法？
分析：显然处于中央，与其他区域都相接，因此它的地位比较特殊，应优先考虑．本题可分解为三类涂法：用颜色涂；用种颜色涂；用种颜色涂．显然用种颜色涂不可能．
解：本题有三类涂法．
第一类：用种颜色涂，显然有
种涂法．
第二类：用种颜色涂，显然有类涂法：与涂同一色，其余三区各涂一色；与涂同一色，其余三区各涂一色，故涂法种数是
（是指先选出种颜色）．
第三类：用种颜色涂，那么与、与、三部分区域各涂一色，故有
种涂法（
是指先选出种颜色）．
综上，涂法总数是：
种．
说明：给图形涂色问题与具体的图形开关有关，需要仔细分析图形特征．另外，对有些题目，一眼看去好像很繁杂，无从下手；这时我们可以从最简单的研究起，然后逐次研究其他的问题．比如本题最简单的情况是种颜色个区域；复杂的情况是种颜色、种颜色涂个区域．复杂的问题分解之后往往就会变得简单，然后先从最简单的情况研究起——这是一种常用的解题策略．
典型例题十四
例14 填空：
．
解法1：原式
……
解法2：由
．
∴
，∴
．
，
，……，
以上各式都加得：
∴
说明：本题解答过程中应用了公式
，即
要熟悉此公式，注意在相关问题中的应用．
典型例题十五
例15 证明下列各等式：
(1) 
；(2) 
；(3) 
．
证明：(1)右边
=左边，∴原式成立．
(2)右边
=左边
∴原式成立．
(3)左边
=右边
∴原式成立．
说明：(1)对于(3)关键一步
变成
有
，再反复运用利用定理2，逐步化简式子即可得证．
(2)也可利用
将等式右边
一项拆成二项，反复使用此公式即可得证．请自己证明．
(3)此题中③式的变形为：
．
典型例题十六
例16 完成下列各填空题：
(1)平面内有
个点，其中个点在一条直线上，此外没有个点在一条直线上，过这个点可以作______________个三角形．
(2)空间
个点，其中个点共面，此外无任何个点共面，这个点可决定多少个不同的平面．
解：(1)把9个点分为两类：
第一类为共线的个点；
第二类为其余的个点；
从第二类中任意选取三个点，可作
个三角形；
从第一类中任意选取一个点，从第二类中任意选取个点，可作
个三角形；
从第一类中任意选取个点，从第二类中任意选取个点，可作
个三角形．
利用分类计数原理，可得总共可作三角形个数为
(个)．
注意：本题也可解为
(个)，请你加以解释．
∴应填：
．
(2)这个问题可分四类加以考虑．
①个共面点决定个平面；
②个共面点中任何个点和其余个点中任意一点决定
个平面；
③个共面点中任一点和其余个点中任意个点决定
个平面；
④个点中任何个点决定
个平面．
总共决定平面的个数为
(个)
∴应填：
说明：这题是利用组合知识解决与几何有关的问题，要注意将已知条件中的元素分成几类．而在解决此问题时，又使用的分类方法，至于怎样确定分类标准，这是一难点，比如，①中确定三角形，必确定不共线的三点．这三点可全部来源于不共线点，也可其一来源于不共线点，还可其二来源于那点，这样分成三类．
典型例题十七
例17 车间有
名工人，其中名男工是钳工，名女工是车工，另外两名老师傅既能当车工又能当钳工，现在要在这名工人里选派名钳工，名车工修理一台机床，问有多少种选派方法．
解法1：设、代表位老师傅．
，都不在内的选法有：
种；
，都在内且当钳工的选法有：
种；
，都在内且当车工的选法有：
种；
，都在内，一人当钳工，一人当车工的选法有：
种；
，有一人在内当钳工的选派方法有：
种；
，有一人在内当车工的选派方法有：
种；
∴共有
(种)．
解法2：名钳工有名选上的派出方法是：
种；
名钳工有名被选上的方法是：
；
名钳工有名被选上的方法是：
种．
∴一共有
(种)
解法3：名女车工都在的选派方法：
种；
名女车工有人在内的派选方法：
种；
名女车工有名在内的派选方法：
种；
∴一共有
(种)．
说明：解法1是以老师傅为主考虑的；解法2是以钳工为主考虑的；解法3是以车工为主考虑的．
典型例题十八
例18 有11名翻译人员，其中5名会英语，4名会日语，另外两名英语、日语都会，从中选出8人，组成两个翻译小组，4人译英语，另4人译日语，同一个人不能参加两个小组，有多少种不同的选派方法？
分析：本题是排列组合应用题中典型的选派问题，本题的困难主要在于对两个语种都会的两个人的处理，由于1个人不能同时参加两个小组，所以1个人不能既充当英语、又充当日语翻译，也就是说本题不能按从7名英语翻译中选4人，从6名日语翻译中取4人来处理，正确解决问题的方法是先就两个语种都会的两个人（特殊元素）的选用情况进行分类．
解：按两个语种都会的两个人的选用情况分类：
两个人都不参加，这时有
种用法．
两个人参加1人，这时还有该人参加英语或日语翻译两种情况，这时有
种用法．
两个人都参加，这时有3种情况，都参加英语、都参加日语、或者分别参加一种．
这时有
种用法．
用分类计数原理，共有不同的选派方法总数为：
(种)．
说明：本题处理起来看似杂乱，分类的情况较多，实际上整个过程都是围绕两名英日语都会的“多面手”的选用进行的，这种抓特殊对象处理的手段在我们组合类应用题中随处可见．
典型例题十九
例19 有6个人住进5个房间，分别按照下列要求，有多少种不同住法？
(1)每个房间至少一个人；
(2)5个房间恰好空出一间不住人．
分析：每个房间至少一个人，则正好一个房间两个人，其它房间各1人，可以先安排两个人进此房间．5个房间空出一间，则有两种可能的结果，一种是一间3个人，3间各1人，另一间空着，还有一种可能结果是有两间各住两人，另两间各住1人，另一间空着．
解：(1)先从6人中选出两人进某一房间，其余4人每人进一间，不同的进房方法共有：
（种）．
(2)按条件不同的住房方法有两类：
第一类：3个人住一间房，3个人各住一间，另一间空，不同的方法共有：
（种）．
第二类：两间房各进两人，另两间各1人，另一间空，不同的进房方法共有：
（种）．
用分类计数原理，所有满足要求的住房方法共有：
（种）．
说明：对于每个房间至少1人的情况，也可能这样考虑，先从6个人中任选5人住进5个房间，最后一人任进一个房间，这样得到的结果是
（种），与上面结果对比，增加了一倍，为什么会出现不同结果呢？原因是这样考虑，住进同一间房的两个人是在两步中分别进入房间的，他们之间产生了不必要的顺序，导致了重复计数，所以对于同一组没有顺序关系的元素在选取时，应该在同一步取到，如果分步取得就会产生顺序．比如：100件产品5件次品，从中任取3件至少一件次品的取法有多少种？我们在计算时不能先从5件次品中先取一件，然后在其它99件中任取2件，列为
，这样的结果中有重复计算的情况．正确的做法是按次品的个数进行分类，l件次2件正：
，2件次1件正：
，三件次，总数为：
（种）．
典型例题二十
例20 有五双不同的鞋，从中任取4只，至少有2只配成一双的可能取法种数是多少？
分析：满足要求的取法有两类，一类是4只中恰有2只配对，还有一类是4只鞋正好配成2双．另外至少有2只配成的一双的反面就是4只均无配对，可以用间接法解题．
解：方法1：如果恰好有两只配成一双，先从5双中取出一双，然后在剩下的四双中取出两双，两双中各取一只，共有取法
种，可以计算得到
（种）．如果四只鞋正好是两双，可以直接从5双鞋中任取两双，共有取法种数为
（种）．
用分类计数原理，所有符合要求的取法有
（种）．
方法2：先从10只鞋中任取4只，有种取法，其中4只鞋都不成对可以看成从5双鞋中取4双，每双取出一只，共有取法
种．用间接法得所有符合条件的取法种数为：
（种）．
说明：对于这种配对问题，我们先处理好成对的元素，再按要求处理其它元素，这实际上也是遵循特殊元素先处理的原则．比如：8个人站成前后两排，每排4人面对面站着，其中某两人必须正对面，有多少种不同排法？我们先选好正对面的两个位置，然后站上这两个人，其它人任意排列，共有排法总数为
（种）．
典型例题二十一
例21 书架上原有6本书，再放过去3本，但要求原有书的相对顺序不改变，则不同的放法有多少种？
分析：本题一方面可以将三本书按步骤逐一放进去．但要注意放第一本书时，它插进去有7种放法，而继续放第二本时，则有8种放法，放第三本时则有9种放法．本题还可从另一方面考虑，当三本书放完后实际上是9本书的一个排列，但原有的六本书按原来的固定顺序，仅考虑它们位于哪六个位置，即只要在9个位置上选出它们的6个位置，而用组合数列式．
解：方法1，按步分别插入3本书，依次有7、8、9种不同放法，不同的放法有
（种）．
方法2：在9个不同的位置放置原有6本书（按原来顺序），然后再在剩下3个位置排另外三本书，不同的放法总数为：
（种）．
说明：在许多排列问题中，有些是有预先给定的确定顺序，有些有隐含的确定顺序．对于这类问题，我们只要选位置、不必排顺序．如：车队有7辆车，现在调出4辆按顺序去执行任务，要求、两车必须出车参加，并且车先于车调出，那么不同的调度方法有多少种？我们可以按下列步骤完成这个问题，先从剩下5辆中调出两辆，选出、两车位置，再排另外两辆，这样不同的调度方法为：
（种）．