典型例题一
例1 解不等式![]()
分析:解含有绝对值的不等式,通常是利用绝对值概念![]() ,将不等式中的绝对符号去掉,转化成与之同解的不含绝对值的不等式(组),再去求解.去绝对值符号的关键是找零点(使绝对值等于零的那个数所对应的点),将数轴分成若干段,然后从左向右逐段讨论.
,将不等式中的绝对符号去掉,转化成与之同解的不含绝对值的不等式(组),再去求解.去绝对值符号的关键是找零点(使绝对值等于零的那个数所对应的点),将数轴分成若干段,然后从左向右逐段讨论.
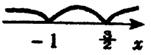
解:令![]() ,∴
,∴ ![]() ,令
,令![]() ,∴
,∴![]() ,如图所示.
,如图所示.
(1)当![]() 时原不等式化为
时原不等式化为![]()
∴![]() 与条件矛盾,无解.
与条件矛盾,无解.
(2)当![]() 时,原不等式化为
时,原不等式化为![]() .
.
∴
![]() ,故
,故![]() .
.
(3)当![]() 时,原不等式化为
时,原不等式化为
![]() .∴
.∴![]() ,故
,故![]() .
.
综上,原不等式的解为![]() .
.
说明:要注意找零点去绝对值符号最好画数轴,零点分段,然后从左向右逐段讨论,这样做条理分明、不重不漏.
典型例题二
例2 求使不等式![]() 有解的
有解的![]() 的取值范围.
的取值范围.
分析:此题若用讨论法,可以求解,但过程较繁;用绝对值的几何意义去求解十分简便.
解法一:将数轴分为![]() 三个区间
三个区间
当![]() 时,原不等式变为
时,原不等式变为![]() 有解的条件为
有解的条件为![]() ,即
,即![]() ;
;
当![]() 时,得
时,得![]() ,即
,即![]() ;
;
当![]() 时,得
时,得![]() ,即
,即![]() ,有解的条件为
,有解的条件为![]() ∴
∴![]() .
.
以上三种情况中任一个均可满足题目要求,故求它们的并集,即仍为![]() .
.
![]()
解法二:设数![]() ,3,4在数轴上对应的点分别为P,A,B,如图,由绝对值的几何定义,原不等式
,3,4在数轴上对应的点分别为P,A,B,如图,由绝对值的几何定义,原不等式![]() 的意义是P到A、B的距离之和小于
的意义是P到A、B的距离之和小于![]() .
.
因为![]() ,故数轴上任一点到A、B距离之和大于(等于1),即
,故数轴上任一点到A、B距离之和大于(等于1),即![]() ,故当
,故当![]() 时,
时,![]() 有解.
有解.
典型例题三
例3 已知![]() ,求证
,求证![]() .
.
分析:根据条件凑![]() .
.
证明:![]()
![]() .
.
说明:这是为学习极限证明作的准备,要习惯用凑的方法.
典型例题四
例4 求证
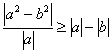
分析:使用分析法
证明
∵![]() ,∴只需证明
,∴只需证明![]() ,两边同除
,两边同除![]() ,即只需证明
,即只需证明
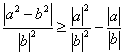 ,即
,即
![]()
当![]() 时,
时,![]() ;当
;当![]() 时,
时,
![]() ,原不等式显然成立.∴原不等式成立.
,原不等式显然成立.∴原不等式成立.
说明:在绝对值不等式的证明,常用分析法.本例也可以一开始就用定理:
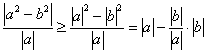
(1)如果![]() ,则
,则![]() ,原不等式显然成立.
,原不等式显然成立.
(2)如果![]() ,则
,则![]() ,利用不等式的传递性知
,利用不等式的传递性知![]() ,
,![]() ,∴原不等式也成立.
,∴原不等式也成立.
典型例题五
例5 求证![]() .
.
分析:本题的证法很多,下面给出一种证法:比较要证明的不等式左右两边的形式完全相同,使我们联想利用构造函数的方法,再用单调性去证明.
证明:设![]() .
.
定义域为{![]() ,且
,且![]() },
},![]() 分别在区间
分别在区间![]() ,区间
,区间![]() 上是增函数.
上是增函数.
又![]() ,
,
∴![]()
即![]()
![]()
∴原不等式成立.
说明:在利用放缩法时常常会产生如下错误:
∵![]() ,
,![]() ,
,
∴![]()
![]() .
.
错误在不能保证![]() ,
,![]() .绝对值不等式
.绝对值不等式![]() 在运用放缩法证明不等式时有非常重要的作用,其形式转化比较灵活.放缩要适度,要根据题目的要求,及时调整放缩的形式结构.
在运用放缩法证明不等式时有非常重要的作用,其形式转化比较灵活.放缩要适度,要根据题目的要求,及时调整放缩的形式结构.
典型例题六
例6 关于实数![]() 的不等式
的不等式![]() 与
与![]()
![]() 的解集依次为
的解集依次为![]() 与
与![]() ,求使
,求使![]() 的
的![]() 的取值范围.
的取值范围.
分析:分别求出集合![]() 、
、![]() ,然后再分类讨论.
,然后再分类讨论.
解:解不等式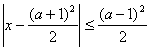 ,
,
![]() ,
,
∴![]() .
.
解不等式![]() ,
,![]() .
.
当![]() 时(即
时(即![]() 时),得
时),得![]() .
.
当![]() 时(即
时(即![]() 时),得
时),得![]() .
.
当![]() 时,要满足
时,要满足![]() ,必须
,必须![]() 故
故![]() ;
;
当![]() 时,要满足
时,要满足![]() ,必须
,必须![]()
![]()
∴![]() .
.
所以![]() 的取值范围是
的取值范围是![]() .
.
说明:在求满足条件![]() 的
的![]() 时,要注意关于
时,要注意关于![]() 的不等式组中有没有等号,否则会导致误解.
的不等式组中有没有等号,否则会导致误解.
典型例题七
例6 已知数列通项公式![]() 对于正整数
对于正整数![]() 、
、![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
分析:已知数列的通项公式是数列的前![]() 项和,它的任意两项差还是某个数列的和,再利用不等式
项和,它的任意两项差还是某个数列的和,再利用不等式![]() ,问题便可解决.
,问题便可解决.
证明:∵![]()
∴![]()
![]()
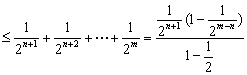
![]() .
.
说明:![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比,共有
为公比,共有![]() 项的等比数列的和,误认为共有
项的等比数列的和,误认为共有![]() 项是常见错误.
项是常见错误.
正余弦函数的值域,即![]() ,
,![]() ,是解本题的关键.本题把不等式、三角函数、数列、
,是解本题的关键.本题把不等式、三角函数、数列、![]() 个变量的绝对值不等式问题连在一起,是一个较为典型的综合题目.如果将本题中的正弦改为余弦,不等式同样成立.
个变量的绝对值不等式问题连在一起,是一个较为典型的综合题目.如果将本题中的正弦改为余弦,不等式同样成立.
典型例题八
例8 已知![]() ,
,![]() ,求证:
,求证:![]()
分析:本题中给定函数![]() 和条件
和条件![]() ,注意到要证的式子右边不含
,注意到要证的式子右边不含![]() ,因此对条件
,因此对条件![]() 的使用可有几种选择:(1)直接用;(2)打开绝对值用
的使用可有几种选择:(1)直接用;(2)打开绝对值用![]() ,替出
,替出![]() ;(3)用绝对值的性质
;(3)用绝对值的性质![]() 进行替换.
进行替换.
证明:∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴![]() ,
,
∴![]()
![]()
![]()
![]()
![]() ,
,
即![]() .
.
说明:这是绝对值和函数的综合题,这类题通常要涉及绝对值及绝对值不等式的性质等综合知识的运用.分析中对条件![]() 使用时出现的三种可能是经常碰到的,要结合求证,灵活选用.
使用时出现的三种可能是经常碰到的,要结合求证,灵活选用.
典型例题九
例9 不等式组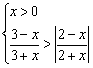 的解集是( ).
的解集是( ).
A.![]() B.
B.![]()
C.![]() D.
D.![]()
分析:本题是考查含有绝对值不等式的解法,由![]() ,知
,知![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,解原不等式组实为解不等式
,解原不等式组实为解不等式![]() (
(![]() ).
).
解法一:不等式两边平方得:![]() .
.
∴![]() ,即
,即![]() ,
,
∴![]() ,又
,又![]() .
.
∴![]() ∴
∴![]() .选C.
.选C.
解法二:∵![]() ,∴可分成两种情况讨论:
,∴可分成两种情况讨论:
(1)当![]() 时,不等式组化为
时,不等式组化为![]() (
(![]() ).
).
解得![]() .
.
(2)当![]() 时,不等式组可化为
时,不等式组可化为![]() (
(![]() ),
),
解得![]() .
.
综合(1)、(2)得,原不等式组的解为![]() ,选C.
,选C.
说明:本题是在![]() 的条件下,解一个含绝对值的分式不等式,如何去绝对值是本题的关键所在,必须注意,只有在保证两边均为非负数时,才能将不等式两边同时平方.另一种方法则是分区间讨论,从而去掉绝对值符号.当然本题还可用特殊值排除法求解.
的条件下,解一个含绝对值的分式不等式,如何去绝对值是本题的关键所在,必须注意,只有在保证两边均为非负数时,才能将不等式两边同时平方.另一种方法则是分区间讨论,从而去掉绝对值符号.当然本题还可用特殊值排除法求解.
典型例题十
例10 设二次函数![]() (
(![]() ,且
,且![]() ),已知
),已知![]() ,
,![]() ,
,![]() ,
,![]() ,当
,当![]() 时,证明
时,证明![]() .
.
分析:从![]() 知,二次函数的图像是开口向上的抛物线;从
知,二次函数的图像是开口向上的抛物线;从![]() 且
且![]() ,
,![]() 知,要求证的是
知,要求证的是![]() ,所以抛物线的顶点一定在
,所以抛物线的顶点一定在![]() 轴下方,取绝对值后,图像翻到
轴下方,取绝对值后,图像翻到![]() 轴上方.因此抛物线的顶点的取值非常重要,也是解这道题的关键所在.
轴上方.因此抛物线的顶点的取值非常重要,也是解这道题的关键所在.
证明:∵![]()
![]()
![]()
![]() ,
,
∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∴![]() .
.
又![]() ,
,![]() ,
,
∴![]()
![]() .
.
而![]() 的图像为开口向上的抛物线,且
的图像为开口向上的抛物线,且![]() ,
,![]() ,
,
∴![]() 的最大值应在
的最大值应在![]() ,
,![]() 或
或![]() 处取得.
处取得.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
说明:本题考查了绝对值不等式的性质、二次函数的最值及分类讨论的思想和逻辑思维的能力,关键是通过对参数![]() ,
,![]() ,
,![]() 的分析,确定抛物线顶点的取值范围,然后通过比较求出函数在
的分析,确定抛物线顶点的取值范围,然后通过比较求出函数在![]() 范围内的最大值.
范围内的最大值.