典型例题一
例1 同时掷四枚均匀硬币,求:
(1)恰有两枚“正面向上”的概率;
(2)至少有两枚“正面向上”的概率.
分析:同时任意投掷四枚均匀硬币,每个硬币的结果都有两种可能性,四枚硬币的情况决定了一次试验的结果,每种结果的出现是等可能的,本$月于等可能事件的概率问题.四枚硬币发生的结果总数我们可以分步确定,恰有两枚正面向上,可以先确定哪两枚正面向上,则另两枚反面向上,至少有两枚正面向上可分类为两枚正面向上、三校正面向上、全部正面向上.
解:同时投掷四枚硬币,正面、反面向上的不同结果总数为:
![]() (种)
(种)
(1)恰有两枚正面向上的结果总数为![]() ,
,
所以恰有两枚正面向上的概率为![]() .
.
(2)至少有两枚正面向上的结果总数为:
![]() 种
种
所以至少两枚正面向上的概率为![]() .
.
说明:使用等可能事件概率公式时,首先要判定事件是不是等可能事件,本题实际上可推广到投掷几枚硬币,恰好有m枚正面向上的概率以及至少有m枚正面向上的概率,设两个事件分别为A、B,可以求到:![]() .
.
典型例题二
例2 用4个不同的球任意投入4个不同的盒子内,每盒投入的球数不限,计算;
(l)无空盒的概率,(2)恰好有一空盒的概率.
分析:一次试验的结果是每个球分别在哪个盒子,由于一个球投入哪一个盒中是任意的,所以一次试验的各个结果是等可能的,本题是等可能事件的概率问题,4个不同小球投入4个盒子的结果总数可以用分步计数原理求得,无空盒的情况实质上相当于每个小球在一个盒中,每个盒子一个球,也就是把4个小球“分配到”4个不同的盆中,信有一个空盒的情况相当于有一个盒子两个球,还有两个盒子各1球,至于它们各自的结果总数可以用排列组合的方法解决.
解:本题是等可能事件的概率问题,4个不同的小球投入四个盆子的所有不同的结果总数为:![]() .
.
(l)无空盒的结果总数为![]() .
.
所以无空盒的概率为![]() .
.
(2)恰有一个空盒,则必有一盒2球,另有两盒各1球,其所有可能结果总数为:
![]() .
.
所以恰有一空盒的概率为:![]() .
.
说明:由于每个小球投入哪一个盒子是任意的,从而导致4个小球投入4个盒子的不同结果是等可能的,现在把球换成人,盒子换成房间,则问题就转变成了若干人任意住进若干个房间的问题,这就是古典概率中有名的“分房问题”.
典型例题三
例3 有6个房间安排4个旅游者住宿,每人可以随意进哪一间,而且一个房间也可以住几个人.试求下列事件的概率.
(1)事件A:指定的4个房间中各有1人;
(2)事件B:恰有4个房间中各有1人;
(3)事件C:指定的某个房间中有两人;
(4)事件D:第1号房间有1人,第2号房间有3人.
分析:由于每个人进哪一个房间是随意的,所以4个人住房的各种结果是等可能的,本题是等可能事件的概率问题.所有可能的不同住房结果总数可以用分步计数原理求得,每人住房的结果都有6种可能,最后4个人住房的不同结果总数为![]() .事件A中指定的4个房间中各有1人相当于4个人排到4个房间中去,有
.事件A中指定的4个房间中各有1人相当于4个人排到4个房间中去,有![]() 种不同结果;事件B中恰有4个房间,每间1人与事件A的区别在于哪4间房不空;事件C中指定的某房间2人,我们可以先从4人中选2人进入此房间,其它2人分步任意住进其它5个房间;事件D可以先安排1号房间1人,再安排2号房间3人
种不同结果;事件B中恰有4个房间,每间1人与事件A的区别在于哪4间房不空;事件C中指定的某房间2人,我们可以先从4人中选2人进入此房间,其它2人分步任意住进其它5个房间;事件D可以先安排1号房间1人,再安排2号房间3人
解:4个人住进6个房间,所有可能的住房结果总数为:
![]() (种)
(种)
(1)指定的4个房间每间1人共有![]() 种不同住法.
种不同住法.
∴![]() .
.
(2)恰有4个房间每间1人共有![]() 种不同住法.
种不同住法.
∴![]() .
.
(3)指定的某个房间两个人的不同的住法总数为:
![]() (种),
(种),
∴![]() .
.
(4)第一号房间1人,第二号房间3人的不同住法总数为:
![]() (种),
(种),
∴![]() .
.
说明:“分房问题”抽象化以后可以与许多问题发生联系,比如,前面例题的小球投入盒子、安排几个人做某几项工作,几列火车停在哪个站道,若干个同学各自在哪一天生日等等.我们可以看例子:某班有50名同学,一年按365天计算,至少有两名同学在同一天生日的概率是多少?50名同学相当于上述例题中的旅游者,每一天相当于“房间”,50名同学所有生日的不同结果总数为:![]() ,至少有两名同学在同一天生日的结果总数可用间接法计算,总数为
,至少有两名同学在同一天生日的结果总数可用间接法计算,总数为![]() ,则至少有两人在同一天生日的概率为
,则至少有两人在同一天生日的概率为![]() ,利用工具计算后将会发现,这是一个很接近1的结果,即50个人的一个班级中,有两个人在同一天生日的概率很大,高达0.97,几乎是令人惊讶的结果.
,利用工具计算后将会发现,这是一个很接近1的结果,即50个人的一个班级中,有两个人在同一天生日的概率很大,高达0.97,几乎是令人惊讶的结果.
典型例题四
例4 某人有5把钥匙,其中有一把是打开房门的钥匙,但他忘记了哪一把是打开房门的钥匙,于是他逐把不重复地试开,问:
(1)恰好第三次打开房门锁的概率是多少?
(2)三次内打开房门锁的概率是多少?
分析:某人五次顺次拿出钥匙的结果相当于5把钥匙的一个排列,由于他每次拿哪一把是任意的,所以不同的拿钥匙的结果的可能性相同,本题是等可能事件的概率问题.恰好第三次打开房门锁相当于第三次拿出的钥匙正好是房门钥匙,或者说在5把钥匙的一个排列中第3把钥匙正好是开房门钥匙,三次内打开房门相当于5把钥匙的排列中,开房门钥匙出现在前3个.
解:本题是等可能事件的概率问题,某人5次拿钥匙的所有不同的结果是![]() .
.
(1)恰好第3次拿出开房门钥匙的结果总数为:![]() .
.
所以恰好第3次打开房门的概率为:
![]()
(2)前3次内拿出开房门钥匙的结果总数为:3![]() .
.
所以前3次打开房门的概率为:
![]()
说明:如果5把钥匙中有2把可以开房门的钥匙,则在前3次内打开房门的概率是多少?三次内找开房门说明在前三次中至少有1次取出开房门钥匙,我们可以通过分类讨论,恰有一把开房门钥匙在前3次拿出的结果总数为:![]() ,恰有两把开房门钥匙在前3次拿出的结果总数为
,恰有两把开房门钥匙在前3次拿出的结果总数为![]() ,这样我们得到前三次内打开房门的结果总数为
,这样我们得到前三次内打开房门的结果总数为![]() ,从而前3次内打开房门的概率为:
,从而前3次内打开房门的概率为:![]() .
.
典型例题五
例5 抽签口语测试,共有a+b张不同的考签,每个考生抽1张考签,抽过的考签不再放回,某考生只会考其中的a张,他是第k个抽签的,求该考生抽到会考考签的概率.
分析:因为每个人抽哪一张考签是随意的,所有人抽签后抽出的结果相当于这些考签的一个全排列,而且各种不同的排列结果出现的可能性相同,本题是求等可能事件的概率问题.由于某考生是第是次抽签,他能抽到会考考签相当于全排列中第k个元素,是某人会考的a个考签中的一个,我们可以用排列组合知识求出这种排列的所有不同种数,然后用等可能事件的概率公式求解.
解:本题是等可能事件的概率问题.a+b个考生的所有不同的抽签结果的总数
为![]() ,
,
某个考生第k次抽签,他正好抽到会考的a张考签的一个,相当于所有抽签的结果中第k张考签是a张考签中的1张,我们可以得到所有这种抽签结果的总数为:![]() .
.
所以某个考生抽到会考考签的概率为:![]() .
.
说明:从计算结果看,第几次抽签对该考生抽到会考考签的概率并没有影响,也就是说,无论他是第几个抽签,都不会影响他抽到会考考签的可能性.在日常生活中有这样的问题:10张彩票中有1张是中奖彩票,现在10个人去摸彩,先模后摸对中奖的可能性有无影响?现在我们可以来计算这个问题的结果,现在假定你是第m个去摸奖,为了计算中奖的概率,先算出10个人摸彩的所有可能结果是10!,而中奖彩票正好出现在第m个的所有可能结果为9!,这样可以得出你中奖的概率为![]() ,结果与m并无关系,根本无须担心中奖彩票被别人抓去.
,结果与m并无关系,根本无须担心中奖彩票被别人抓去.
典型例题六
例6 已知10只晶体管中有8只正品,2只次品,每次任抽取1只测试,测试后放回,求下列事件的概率.
(1)抽3次,第3只是正品;
(2)直到第6只时,才把2只次品都捡到了.
分析:每次从10件晶体管中任取1件,经过若干次,各种结果的可能性是一样的,抽 3次,所有可能抽出的结果总数为10×10×10,抽6次,所有可能抽出的结果总数为![]() ,到第6次时正好第2只次品也抽到了,说明前5次抽检中出现过另一只次品,当然这只次品也可能出现过几次.我们可以用间接法来求出符合这个要求的所有可能结果的总数为
,到第6次时正好第2只次品也抽到了,说明前5次抽检中出现过另一只次品,当然这只次品也可能出现过几次.我们可以用间接法来求出符合这个要求的所有可能结果的总数为![]() ,这个式子的含义是先走下第6次抽出的次品是哪一个,然后用前5次抽检的所有结果总数(前5次未出现第6次抽检的次品)减去前5次全是正品的所有结果总数.
,这个式子的含义是先走下第6次抽出的次品是哪一个,然后用前5次抽检的所有结果总数(前5次未出现第6次抽检的次品)减去前5次全是正品的所有结果总数.
解:本题是等可能事件的概率问题.
(1)抽检3次所有可能的抽检结果总数为![]() ,
,
第三只是正品的所有可能的抽检结果总数为10×10×8.
所以第三只是正品的概率为:![]() .
.
(2)抽检6次所有可能的抽检结果总数为![]() .
.
∵ 第6只时才能把第2只次品抽检到,
∴ 前5次抽检未出现第6次抽到的次品,但是至少出现一次另一只次品.
∴ 第6只时才把第2只次品抽检到的所有可能的抽检结果总数为 ![]() .
.
此事件发生的概率为:
![]() .
.
说明:如果每次抽检的结果不再放回去,直到第6只时才把2只次品都找出来的概率是多少?这个问题仍然是等可能事件的概率问题,因为抽出的产品不再拿回,所以前6次抽出的不同结果相当于从10件产品中抽出6件的一个排列,所有可能的结果总数为![]() ,第6次抽到第2件次品,说明第6件是次品,前面还有一件次品,所有可能的结果总数为
,第6次抽到第2件次品,说明第6件是次品,前面还有一件次品,所有可能的结果总数为![]() ,其含义是先在第6个位置放一个次品,另一个次品在前面5个位置的某一个上,最后在其它四个位置上放上8件正品中的4个.用等可能事件的概率公式可算出此事件发生的概率是
,其含义是先在第6个位置放一个次品,另一个次品在前面5个位置的某一个上,最后在其它四个位置上放上8件正品中的4个.用等可能事件的概率公式可算出此事件发生的概率是![]() .
.
典型例题七
例7 求100件产品中,有95件合格品,5件次品.从中任取3件,求:
(1)3件都是合格品的概率;
(2)3件都是次品的概率;
(3)2件是合格品、1件是次品的概率.
分析:可从集合的角度处理本题.需求出全集![]() 的元素个数及
的元素个数及![]() 中各子集的元素个数.
中各子集的元素个数.
解:从100件产品中任取3件可能出现的结果数,就是从100个元素中任取3个元素的组合数![]() .由于是任意抽取,这些结果出现的可能性都相等.
.由于是任意抽取,这些结果出现的可能性都相等.
(1)由于在100件产品中有95件合格品,取到3件合格品的结果数,就是从95个元素中任取3个元素的组合数![]() ,记“任取3件,它们都是合格品”为事件
,记“任取3件,它们都是合格品”为事件![]() ,那么事件
,那么事件![]() 的概率:
的概率:
![]() .
.
得![]() 件都是合格品的概率为
件都是合格品的概率为![]() .
.
(2)由于在100件产品中有5件次品,取到3件次品的结果数,就是从5个元素中任取3个元素的组合数![]() .记“任取3件,它们都是次品”为事件
.记“任取3件,它们都是次品”为事件![]() ,那么事件
,那么事件![]() 的概率:
的概率:
![]() .
.
得3件都是次品的概率为![]() .
.
(3)记“任取3件,其中2件是合格品、1件是次品”为事件![]() .由于在
.由于在![]() 种结果中,取到2件合格品、1件次品的结果有
种结果中,取到2件合格品、1件次品的结果有![]() 种,故事件
种,故事件![]() 的概率:
的概率:
![]()
得2件合格品、1件是次品的概率为![]() .
.
说明:本题是产品抽取问题.抽取时,抽到其中的任何一件产品的可能性都相等,可用等可能事件的概率公式进行计算.
典型例题八
例8 现有一批产品共有10件,其中8件为正品,2件为次品.
(1)如果从中取出一件,然后放回,再任取一件然后放回,再任取一件,求连续3次取出的都是正确的概率.
(2)如果从中一次取3件,求3件都是正品的概率.
解:(1)为返回抽样问题,每次抽样都有10种可能,根据分步计数原理,所有等可能出现的结果为![]() 种,设
种,设![]() 表示“三次返回抽样,所抽得的3件产品都是正品”,则
表示“三次返回抽样,所抽得的3件产品都是正品”,则![]() 所包含的结果根据分步计数原理有
所包含的结果根据分步计数原理有![]() 种.
种.
∴![]() .
.
(2)为不返回抽样问题,所有等可能出现的结果为![]() 种,设
种,设![]() 表示“一次抽3件,所抽得的产品都是正品”,则
表示“一次抽3件,所抽得的产品都是正品”,则![]() 所包含的结果有
所包含的结果有![]() ,所以,
,所以,![]()
说明:求等可能事件的概率,在求![]() 时应注意
时应注意![]() 种结果必须是等可能的,例如抛掷2枚均匀硬币,共出现
种结果必须是等可能的,例如抛掷2枚均匀硬币,共出现![]() 种可能结果,如果认为只有“2个正面”、“2个反面”、“1正1反”这3种结果,那么显然这3种结果不是等可能的.
种可能结果,如果认为只有“2个正面”、“2个反面”、“1正1反”这3种结果,那么显然这3种结果不是等可能的.
典型例题九
例9 箱中有![]() 个正品,
个正品,![]() 个次品,从箱中随机连续抽取3次,每次取1个,取出后不放回,问取出的3个全是正品的概率是多少?
个次品,从箱中随机连续抽取3次,每次取1个,取出后不放回,问取出的3个全是正品的概率是多少?
分析1:可以看作不放回抽样3次有顺序.
解法1:从![]() 个产品中不放回抽样有顺序,共有
个产品中不放回抽样有顺序,共有![]() 种方法,从
种方法,从![]() 个正品中不放回抽样3次有顺序,共有
个正品中不放回抽样3次有顺序,共有![]() 种不同抽法,可以取出3个正品的概率
种不同抽法,可以取出3个正品的概率![]() .
.
分析2:可以看作不放回抽样3次无顺序.
解法2:从![]() 个产品中不放回抽样3次无顺序,共有
个产品中不放回抽样3次无顺序,共有![]() 种方法,从
种方法,从![]() 个正品中取出3个正品的取法有
个正品中取出3个正品的取法有![]() ,所求概率为:
,所求概率为:![]() .
.
说明:关于不放回抽样可以看作有顺序(即排列问题),也可看作无顺序(组合问题),其结果是一样的.不论选用哪种方式,确定之后必须按同一方式去解决,否则会产生错误.
典型例题十
例10 5人并排坐在一起照像,计算:
(1)甲恰好坐在正中间的概率;
(2)甲、乙两人恰好坐在一起的概率;
(3)甲、乙两人恰好坐在两端的概率;
(4)甲坐在中间、乙坐在一端的概率.
分析:5人并排坐在一起照像,可有![]() 不同的坐法,这些坐法出现的可能性都是相等的,本题利用等可能事件的概率求解.
不同的坐法,这些坐法出现的可能性都是相等的,本题利用等可能事件的概率求解.
解:(1)设“甲恰好坐在正中间”的事件为![]() ,则
,则![]() .
.
得到甲恰好坐在正中间的概率为![]() .
.
(2)“甲、乙两人恰好坐在一起”的事件为![]() ,则
,则![]() .
.
得到甲、乙两人恰好坐在一起的概率为![]() .
.
(3)设“甲、乙两人恰好坐在两端”的事件为![]() ,则
,则![]() .
.
得到甲、乙两人恰好坐在两端的概率为![]() .
.
(4)设“甲坐在中间、乙坐在一端”的事件为![]() ,则
,则![]() .
.
得到甲坐在中间、乙坐在一端的概率为![]() .
.
典型例题十一
例11 一副扑克牌有红桃、黑桃、梅花、方块4种花色,每种13张,共52张,从一副洗好的牌中任取4张,求4张中至少有3张黑桃的概率.
分析:至少有3张黑桃包括两种情况:“恰有3张黑桃”与“4张全是黑桃”.用这两种情况的取法总数除以52张牌中任取4张牌的取法总数.
解:从52张牌中任取4张,有![]() 种取法,即
种取法,即![]() .
.
4张牌中至少有3张黑桃的取法有![]() .
.
因此,取4张牌中至少有3张黑桃的概率是:![]() .
.
说明:(1)若先取3张黑桃,有![]() 种取法,第4张黑桃从剩余49张中任取1张,这样所求概率为
种取法,第4张黑桃从剩余49张中任取1张,这样所求概率为![]() .错误原因在于分子计算中有重复现象.
.错误原因在于分子计算中有重复现象.
(2)“至多”与“至少”的组合数可用分类法或排除法求.本例中可用52张中取4张的全部取法![]() 减去没有黑桃的取法
减去没有黑桃的取法![]() ,再减去恰有一张黑桃的取法
,再减去恰有一张黑桃的取法![]() ,再减去恰有2张黑桃的取法
,再减去恰有2张黑桃的取法![]() ,得
,得![]() 求得.
求得.
典型例题十二
例12 某大学招收的15名新生中有3名优秀生,随机将15名新生平均分配到3个班中去.
(1)每班各分配到一名优秀生的概率是多少?
(2)3名优秀生分配到同一班的概率是多少?
分析(1):每班分配到1名优秀生和4名非优秀生,甲班从3名优秀生中任选1名,从12名非优秀生中任选4名,共有![]() 种方法;乙班从剩下的2名优秀生中选1人,从剩下的8名非优秀生中选4名,共有
种方法;乙班从剩下的2名优秀生中选1人,从剩下的8名非优秀生中选4名,共有![]() 种方法;最后剩下的1名优秀生和4名非优秀生给丙班.有
种方法;最后剩下的1名优秀生和4名非优秀生给丙班.有![]() 种方法.将15名新生平均分到甲、乙、丙三个班级共有
种方法.将15名新生平均分到甲、乙、丙三个班级共有![]() 种不同的分法.
种不同的分法.
解:每个班级分到1名优秀生,共有![]() 种不同的方法,将15名学生平均分到3个班级共有
种不同的方法,将15名学生平均分到3个班级共有![]() 种不同方法,每班分配到1名优秀生的概率.
种不同方法,每班分配到1名优秀生的概率.
![]() .
.
分析(2):3名优秀生都分到甲班,共有![]() 种分法,乙班从剩下的10名之中选5名
种分法,乙班从剩下的10名之中选5名![]() ,剩下5名给丙班,共有
,剩下5名给丙班,共有![]() 种不同分法.同理,3名优秀生都分到乙班、丙班方法数均为
种不同分法.同理,3名优秀生都分到乙班、丙班方法数均为![]() .
.
解:3名优秀生都分到同一班级的概率为![]() .
.
典型例题十三
例13 “齐鲁福利风采”彩票的模奖办法是![]() 选
选![]() ,即每一注彩票都是从
,即每一注彩票都是从![]() 中选
中选![]() 个数构成。开奖时,先摇出
个数构成。开奖时,先摇出![]() 个基本号码,再摇出
个基本号码,再摇出![]() 个特殊号码.中奖方法如下:一等奖,所选
个特殊号码.中奖方法如下:一等奖,所选![]() 个号码全部为基本号码;二等奖:所选
个号码全部为基本号码;二等奖:所选![]() 个号码中有
个号码中有![]() 个是基本号码,而另一个必须是特殊号码(即
个是基本号码,而另一个必须是特殊号码(即![]() );三等奖:所选
);三等奖:所选![]() 个号码中有
个号码中有![]() 个是基本号码,另一个随便;四等奖:所选
个是基本号码,另一个随便;四等奖:所选![]() 个号码中有
个号码中有![]() 个是基本号码,
个是基本号码,![]() 个是特殊号码,另外
个是特殊号码,另外![]() 个号码随便(即
个号码随便(即![]() ),依次类推.某人花
),依次类推.某人花![]() 元钱投了一注彩票,试计算该注彩票获一等奖、二等奖、三等奖的概率分别是多少?
元钱投了一注彩票,试计算该注彩票获一等奖、二等奖、三等奖的概率分别是多少?
分析:这是一个典型的等可能性事件的概率问题,只需计算出![]() 、
、![]() 即可:投一注彩票,即是从
即可:投一注彩票,即是从![]() 个号码中选出
个号码中选出![]() 个号码.
个号码.
解:从![]() 个号码中选出
个号码中选出![]() 个,即构成一注彩票,所有可能的选法共有
个,即构成一注彩票,所有可能的选法共有![]() 种,即基本事件的总数:
种,即基本事件的总数:![]() .
.
设开奖后摇出的基本号码是![]() ,特殊号码是
,特殊号码是![]() .那么该注彩票获得一等奖的选法只有一种,即只能选
.那么该注彩票获得一等奖的选法只有一种,即只能选![]() ,故
,故![]() ,因此获一等奖的概率为:
,因此获一等奖的概率为:
![]() .
.
该注彩票获二等奖的选法有![]() 种,即
种,即![]() ,因此获二等奖的概率为:
,因此获二等奖的概率为:
![]() .
.
该注彩票获三等奖的选法有:![]() ,即
,即![]() ,因此获三等奖的概率为:
,因此获三等奖的概率为:
![]() .
.
说明:在日常生活中有很多现象都是随机现象,都可以用概率的知识来解释.在学习中应有意识地将所学知识运用于实际,既可提高学习兴趣,又可使自己的数学应用能力得到提高.
典型例题十四
例14 甲、乙二人参加法律知识竞答,共有![]() 道不同的题目,其中选择题
道不同的题目,其中选择题![]() 道,判断题
道,判断题![]() 道,甲、乙两人依次各抽一题.
道,甲、乙两人依次各抽一题.
(1)甲抽到选择题、乙抽到判断题的概率是多少?
(2)甲、乙二人中至少有一人抽到选择题的概率是多少?
分析:这也是一个等可能性事件的概率问题,只须算出![]() 、
、![]() .注意这里是“甲、乙二人依次各抽一题”,故
.注意这里是“甲、乙二人依次各抽一题”,故![]() .
.
解:由题意:甲乙两人依次各抽一题,故所有可能的抽法是:
![]() 种.
种.
(1)“甲抽到选择题,乙抽到判断题”的抽法有![]() 种,即
种,即![]() .
.
∴这一事件的概率为![]() .
.
(2)下面计算“甲乙两人中至少有一人抽到选择题”的抽法种数.
(法1)抽法分两类:①只有一人抽一选择题,抽法种数是![]() ;
;
②两人都抽到选择题,抽法种数是![]() 种,故总数为
种,故总数为![]() 种.
种.
(法2)先考虑反面:甲、乙两人都未抽到选择题,即都抽到判断题,则抽法种数是![]() (种),那么“甲、乙两人至少有一人抽到选择题”的抽法即为
(种),那么“甲、乙两人至少有一人抽到选择题”的抽法即为![]() 种.
种.
因此![]() .
.
∴该事件的概率为![]() .
.
说明:本题难度并不大,基本上是直接应用概率公式.关键步骤是应用排列、组合的知识求出![]() 、
、![]() ,即所有可能结果的总数(基本事件的总数)和事件
,即所有可能结果的总数(基本事件的总数)和事件![]() 所包含的结果的总数.
所包含的结果的总数.
典型例题十五
例15 十个号码![]() 号、
号、![]() 号、…,
号、…,![]() 号装于一袋中,从中任取三个,问大小在中间的号码恰为
号装于一袋中,从中任取三个,问大小在中间的号码恰为![]() 号的概率是多少?
号的概率是多少?
分析:因每个号码被取出的可能性是相等的,故该题属于等可能性事件的概率.
解:从十个号码中任取三个,所有可能的取法有![]() 种,即
种,即![]() .而三个号码中大小在中间的号码为
.而三个号码中大小在中间的号码为![]() ,即
,即![]() 为中间数,另外两数一个小于
为中间数,另外两数一个小于![]() ,一个大于
,一个大于![]() ,这样的取法有
,这样的取法有![]() 种,即
种,即![]() .
.
∴所求事件的概率是![]() .
.
说明:利用等可能事件的定义求概率,不要忘记等可能事件的两大特征:基本事件总数有限及基本事件的发生等可能.本部分的题目都属这种类型,即简单而又常用的古典概型.
典型例题十六
例16 同时抛掷两枚相同的骰子(每个面上分别刻有![]() 个点数,抛掷后,以向上一面的点数为准),试计算出现
个点数,抛掷后,以向上一面的点数为准),试计算出现![]() 点、
点、![]() 点、
点、![]() 点的概率是多少?
点的概率是多少?
分析:属等可能性事件.为简单明了起见,可以认为两只骰子是编了号的、不同的骰子.
解:将两只骰子编号为![]() 号、
号、![]() 号,同时抛掷,则可能出现的情况有
号,同时抛掷,则可能出现的情况有![]() 种,即
种,即![]() .
.
出现![]() 点的情况有
点的情况有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ;∴概率为
;∴概率为![]() .
.
出现![]() 点的情况有
点的情况有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴概率为
,∴概率为![]() .
.
出现![]() 点的情况有
点的情况有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,∴概率为
,∴概率为![]() .
.
说明:骰子是用来赌博的工具,赌博中也有不少的学问.事实上“概率论”就起源于![]() 世纪中叶风行欧洲的赌博活动.我们用概率的知识可以揭穿赌博中“输赢”的实质:虽然都是随机现象,但发生的概率是不一样的.如该题中出现
世纪中叶风行欧洲的赌博活动.我们用概率的知识可以揭穿赌博中“输赢”的实质:虽然都是随机现象,但发生的概率是不一样的.如该题中出现![]() 点的概率就最大,因此赢的可能性就最大.还可以计算出现
点的概率就最大,因此赢的可能性就最大.还可以计算出现![]() 点和
点和![]() 点的概率最小,都是
点的概率最小,都是![]() ,因此赢的可能性最小.
,因此赢的可能性最小.
典型例题十七
例17 有一摆地摊的赌主,拿了![]() 个白的、
个白的、![]() 个黑的围棋子放在一个布袋中,他精心绘制了一张中彩表:凡愿摸彩者,每人每次交
个黑的围棋子放在一个布袋中,他精心绘制了一张中彩表:凡愿摸彩者,每人每次交![]() 元“手续费”,然后一次从袋中摸出
元“手续费”,然后一次从袋中摸出![]() 个棋子,中彩情况如下表所列.
个棋子,中彩情况如下表所列.
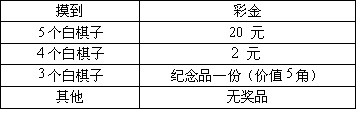
问:按摸![]() 次统计,赌主可净赚多少钱?
次统计,赌主可净赚多少钱?
分析:在试验次数足够多时,事件发生的频率将近似地等于其固有概率.因此我们可以将各个事件的概率(即中彩概率)近似地代替现实情景中事件真实发生的频率.
解:容易算出,摸到![]() 个白子的概率为
个白子的概率为![]() ;摸到
;摸到![]() 个白子的概率为
个白子的概率为![]() ;摸到
;摸到![]() 个白子的概率为
个白子的概率为![]() .按照
.按照![]() 次摸彩来计算,赌主手续费收入为
次摸彩来计算,赌主手续费收入为![]() 元,而他支付的彩金(包括纪念品)大约是:
元,而他支付的彩金(包括纪念品)大约是:
![]() (元).即每摸
(元).即每摸![]() 次彩,赌主可净赚
次彩,赌主可净赚![]() 元左右.
元左右.
说明:摸彩虽是一种“机会游戏”,可能有的人较幸运,摸中头彩,但这样的情况不会很多,事件的发生是受内部规律性制约的.当摸彩次数越多,情况就越接近理论值,将事件发生的概率乘以摸彩次数,即得到该事件发生的次数(理论值,实际值可能在这个值附近波动).由此可推算出赌主的获利情况.当然,赌主总是最后的赢家.
典型例题十八
例18 袋中有![]() 只黑球,
只黑球,![]() 只白球,它们除颜色不同外,没有其他差别.现在把球随机地一只一只摸出来,求第
只白球,它们除颜色不同外,没有其他差别.现在把球随机地一只一只摸出来,求第![]() 次摸出的球是黑球的概率(
次摸出的球是黑球的概率(![]() ).
).
分析:![]() 只球随机摸出,属古典概型.但由于选取的基本事件全体不同,可产生不同的解法.
只球随机摸出,属古典概型.但由于选取的基本事件全体不同,可产生不同的解法.
解法一:把只考虑第![]() 次摸出球的每一种可能作为基本事件.不妨设
次摸出球的每一种可能作为基本事件.不妨设![]() 只球都编上了号码:
只球都编上了号码:![]() .当第
.当第![]() 次摸球时,每只球都有摸到的可能,故第
次摸球时,每只球都有摸到的可能,故第![]() 次摸出球的所有可能有
次摸出球的所有可能有![]() 种(特殊地,可考虑当
种(特殊地,可考虑当![]() 时的情形,此时较易理解),即本事件总数为
时的情形,此时较易理解),即本事件总数为![]() ,而第
,而第![]() 次摸到黑球所包含的基本事件数为
次摸到黑球所包含的基本事件数为![]() ,故
,故
![]() .
.
解法二:把![]() 只球都看作是不同的(设编号为
只球都看作是不同的(设编号为![]() ).我们假想袋中的
).我们假想袋中的![]() 只球全部排成了一列,则摸球时从一端开始依次取一只球即可,直至把球全部取完,这样,
只球全部排成了一列,则摸球时从一端开始依次取一只球即可,直至把球全部取完,这样,![]() 只球的一种排法就对应着一种摸法.我们把
只球的一种排法就对应着一种摸法.我们把![]() 只球所有不同的排法作为基本事件全体,其总数为
只球所有不同的排法作为基本事件全体,其总数为![]() ;第
;第![]() 只球恰为黑球的排法为
只球恰为黑球的排法为![]() .所以,
.所以,
![]() .
.
解法三:把![]() 只球都看作是不同的.将前
只球都看作是不同的.将前![]() 次摸球所有不同的可能作为基本事件全体,其总数为
次摸球所有不同的可能作为基本事件全体,其总数为![]() ,则“第
,则“第![]() 次摸到黑球”所包含的基本事件数为
次摸到黑球”所包含的基本事件数为![]() ,故
,故
![]() .
.
解法四:对同色球不加区别,仍假想袋中的![]() 只球排成了一列,摸球时从一端起一次摸一只,直至摸完.把
只球排成了一列,摸球时从一端起一次摸一只,直至摸完.把![]() 只相同的黑球在
只相同的黑球在![]() 个位置上所有不同的排法作为基本事件全体,其总数为
个位置上所有不同的排法作为基本事件全体,其总数为![]() ,则“第
,则“第![]() 个位置是黑球”所包含的基本事件数为
个位置是黑球”所包含的基本事件数为![]() ,故
,故
![]()
说明:该问题实际上是“抽签原理”的一种推广.抽签有先有后,但对每个抽签者而言,机会都是平等的,即若在![]() 张票中有
张票中有![]() 张奖票,
张奖票,![]() 个人每人抽一张,则每人抽中奖票的概率都是
个人每人抽一张,则每人抽中奖票的概率都是![]() ,与抽票的顺序无关.若在
,与抽票的顺序无关.若在![]() 张票中有
张票中有![]() 张奖票,结论也是一样的,每人抽中奖票的概率都是
张奖票,结论也是一样的,每人抽中奖票的概率都是![]() .因此在该题中,要从
.因此在该题中,要从![]() 个黑球
个黑球![]() 个白球中摸出一个黑球,其概率都是
个白球中摸出一个黑球,其概率都是![]() ,与第几次摸无关.
,与第几次摸无关.
典型例题十九
例19 有![]() 个指定的席位,坐在
个指定的席位,坐在![]() 个席位上的人都不知道自己指定的号码,当这
个席位上的人都不知道自己指定的号码,当这![]() 个人随机地在这
个人随机地在这![]() 个席位上就坐时.
个席位上就坐时.
(1)求![]() 个人中有
个人中有![]() 个人坐在指定的席位上的概率;
个人坐在指定的席位上的概率;
(2)若要这![]() 个人坐在自己指定的席位上的概率不小于
个人坐在自己指定的席位上的概率不小于![]() ,则至多有几个人坐在自己指定的席位上?
,则至多有几个人坐在自己指定的席位上?
分析:![]() 个人坐
个人坐![]() 个位子,共有
个位子,共有![]() 种不同的坐法,每一种坐法可作为一个基本事件.
种不同的坐法,每一种坐法可作为一个基本事件.
解:取![]() 个人坐
个人坐![]() 个位子所有可能的坐法为基本事件全体,则基本事件总数为
个位子所有可能的坐法为基本事件全体,则基本事件总数为![]() .
.
(1)“![]() 个人中有
个人中有![]() 个人坐在自己指定的席位上”,记为事件
个人坐在自己指定的席位上”,记为事件![]() ,它包含的基本事件数为
,它包含的基本事件数为![]() .所以
.所以![]() .
.
(2)“![]() 个人中有
个人中有![]() 个人坐在自己的席位上”,记为事件
个人坐在自己的席位上”,记为事件![]() ,它包含的基本事件数为
,它包含的基本事件数为![]() .
.
所以![]() .
.
故符合题中条件时,至多有![]() 人坐在自己指定的席位上.
人坐在自己指定的席位上.
说明:求概率的题目,找准“基本事件”很重要,因此一定要明确以什么“事件”作为基本事件,某事件![]() 所包含的基本事件必须与此相对应.比如本题以“
所包含的基本事件必须与此相对应.比如本题以“![]() 个人坐
个人坐![]() 个位子”的每一种坐法为一个基本事件(共
个位子”的每一种坐法为一个基本事件(共![]() 个),那么需要计算“有
个),那么需要计算“有![]() 个人坐在指定的位子上”共有多少种坐法:从
个人坐在指定的位子上”共有多少种坐法:从![]() 个人中任选
个人中任选![]() 人(有
人(有![]() 种选法),这
种选法),这![]() 人坐在自己的位子上,坐法就定了,而另外
人坐在自己的位子上,坐法就定了,而另外![]() 人都不坐在自己的位子上,只有
人都不坐在自己的位子上,只有![]() 种坐法,故坐法总数是
种坐法,故坐法总数是![]() .第(2)小题同理.需要注意的一个事实是:坐在自己指定位子上的人越多,其发生的概率就越小,反之概率越大.我们可以凭感觉得出这一结论.因此第(2)小题要求是“至多”有几人坐在自己指定的席位上.
.第(2)小题同理.需要注意的一个事实是:坐在自己指定位子上的人越多,其发生的概率就越小,反之概率越大.我们可以凭感觉得出这一结论.因此第(2)小题要求是“至多”有几人坐在自己指定的席位上.
典型例题二十
例20 有红、黄、蓝三种颜色的旗帜各![]() 面,在每种颜色的
面,在每种颜色的![]() 面旗帜上分别标上号码
面旗帜上分别标上号码![]() ,
,![]() 和
和![]() ,现任取出
,现任取出![]() 面,它们的颜色与号码均不相同的概率是___________.
面,它们的颜色与号码均不相同的概率是___________.
分析一:考虑基本事件的空间是与顺序无关的,分别求出基本事件的总数和发生事件的总数.利用等可能性事件的概率即可求解.
解法一:在所有![]() 面旗帜中任取
面旗帜中任取![]() 面共有
面共有![]() 种取法,若使
种取法,若使![]() 面旗帜的颜色与号码均不相同,则应取红、黄、蓝旗帜各一面,首先取红色旗帜,有
面旗帜的颜色与号码均不相同,则应取红、黄、蓝旗帜各一面,首先取红色旗帜,有![]() 种取法,再取黄色旗帜有
种取法,再取黄色旗帜有![]() 种取法,最后取蓝色旗帜只有
种取法,最后取蓝色旗帜只有![]() 种取法,所以共有
种取法,所以共有![]() 种取法,故所求概率为
种取法,故所求概率为![]() .
.
分析二:考虑基本事件的空间是与顺序有关的.分别求出基本事件的总数与发生事件的总数.由等可能事件的概率即可求解.
解法二:在所有的![]() 面旗帜中任取
面旗帜中任取![]() 面的排列总数有
面的排列总数有![]() 种,使
种,使![]() 面旗帜的颜色与号码均不相同的取法,第
面旗帜的颜色与号码均不相同的取法,第![]() 面有
面有![]() 种取法,第
种取法,第![]() 面有
面有![]() 种取法,第
种取法,第![]() 面有
面有![]() 种取法,由分步计数原理得
种取法,由分步计数原理得![]() 种取法.从而三面旗帜的颜色与号码均不同的概率为
种取法.从而三面旗帜的颜色与号码均不同的概率为![]() .
.
说明:求等可能性事件的概率,关键是正确计算出基本事件和发生事件的总数.同时注意基本事件和发生事件要在同一种空间,如本题的解法一考虑的事件是无序的空间,解法二是在有序的空间.
典型例题二十一
例21 判断下列命题正确与否.
(1)掷两种硬币,可能出现“两上正面”、“两个反面”、“一正一反”![]() 种结果.
种结果.
(2)某袋中装有大小均匀的三个红球、二个黑球、一个白球,那么每种颜色的球被摸到的可能性相同.
(3)从![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中任取一数,取到的数小于
中任取一数,取到的数小于![]() 与不小于
与不小于![]() 的可能性相同.
的可能性相同.
(4)分别从![]() 个男同学,
个男同学,![]() 个女同学中各选一名作代表,那么每个同学当选的可能性相同.
个女同学中各选一名作代表,那么每个同学当选的可能性相同.
(5) ![]() 人抽签,甲先抽,乙后抽,那么乙与甲抽到某号的可能性肯定不同.
人抽签,甲先抽,乙后抽,那么乙与甲抽到某号的可能性肯定不同.
解:以上命题均不正确.
题(1)中应为![]() 种结果,还有一种是“一反一正”;
种结果,还有一种是“一反一正”;
题(2)中摸到红球的概率为![]() ,摸到黑球概率为
,摸到黑球概率为![]() ,摸到白球概率为
,摸到白球概率为![]() ;
;
题(3)取到小于![]() 的概率为
的概率为![]() ,不小于
,不小于![]() 的概率为
的概率为![]() ;
;
题(4)中男同学当选的概率为![]() ,女同学当选的概率为
,女同学当选的概率为![]() ;
;
题(5)中抽签有先有后,但每人抽到某号的概率是相同的.
说明:等可能性事件要求所有结果出现的可能性都相等,强调所有结果,每一结果出现的概率都相同.
典型例题二十二
例22 某篮球运动员在最近几场大赛中罚球投篮的结果如下:
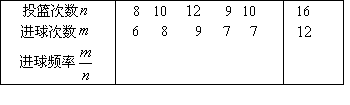
(1)计算表中进球的频率.
(2)这位运动员投篮一次,进球的概率是多少?
解:(1) ![]()
![]()
![]()
![]()
![]()
![]()
(2) ![]()
说明:频率具有稳定性,其值总是在某个常数附近摆动,且随着试验次数的不断增多,这种摆幅度越来越小,而这个常数便是概率,概率可以看作频率在理论上的期望值.