高二必修5《数列》单元测试卷

高二必修5《数列》单元测试卷

一、选择题（每小题3分,共33分）

1、数列的一个通项公式是　　　　　　　　　　　　 

　　A．　　 　　　　　B．

　　C．　　 D．

2、已知数列｛a_n｝的通项公式,则a₄等于( 　　).

　 A　1　　　　 B 2　　　　 C 3　　　　D 0

3、在等比数列中,则(　　)

　　A 　　　　　 B 　　　　　　　C 　　　　　　　 D

4、已知等差数列的公差为2，若，，成等比数列，则等于(　　　)

A　　　　 B 　　　　 C　　　　　　D　

5、等比数列｛a_n｝的前3项的和等于首项的3倍，则该等比数列的公比为　（　　）

A．－2　　　　 B．1　　　　　　C．－2或1　　　D．2或－1

6、等差数列中，已知前15项的和，则等于（　　）．

　　A．　　　　　B．12　　　　　 C．　　　　　D．6

7、已知等比数列{a_n} 的前n项和为S_n ， 若S₄=1，S₈=4，则a₁₃+a₁₄+a₁₅+a₁₆=（　　）．

　　A．7 　　　　　 B．16 　　　　　C．27 　　　　　D．64

8、一个三角形的三个内角A、B、C成等差数列，那么的值是

A．　　　　  　B．　　　　　 C．　　　　　　D．不确定

9、若一个凸多边形的内角度数成等差数列，最小角为100°，最大角为140°，这个凸多边形的边数为

A．6　　　　　　 B．　　　　　　 C．10　　　　　　　 D．12

10、 在等比数列{a_n}中，=1，=3，则的值是　

　　A．14　　　　　 B．16 　　　　　C．18　　 　　　D．20

11、计算机的成本不断降低，若每隔3年计算机价格降低，现在价格为8100元的计算机，9年后的价格可降为（　　　　　 　）

A．2400元　　　　B．900元　　　C．300元　　　　 D．3600元

二、填空题（每小题4分,共20分）

12、已知等比数列｛｝中,=2,=54,则该等比数列的通项公式= 　　　　  

13、 等比数列的公比为2, 且前4项之和等于30, 那么前8项之和等于　　　　 　　

14、数列的前n项和是　　　　 ．

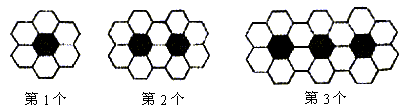
15、 黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：

则第n个图案中有白色地面砖­­­_________________块.

 

 

 

16、在数列中，，且对于任意自然数n，都有，则＝　　　

三、解答题

17、（本小题满分8分）

等差数列中，已知，试求n的值

18、（本小题满分8分）

　　在等比数列中，，公比，前项和，求首项和项数．

19、（本小题满分10分）

已知：等差数列{}中，=14，前10项和．

（1）求；

（2）将{}中的第2项，第4项，…，第项按原来的顺序排成一个新数列，求此数列的前项和．

20、（本小题满分10分）

某城市2001年底人口为500万，人均住房面积为6 m²，如果该城市每年人口平均增长率为1%，则从2002年起，每年平均需新增住房面积为多少万m²，才能使2020年底该城市人均住房面积至少为24m²？(可参考的数据1.01¹⁸=1.20，1.01¹⁹=1.21，1.01²⁰=1.22).

21、（本小题满分11分）

已知等差数列{a_n}的首项a₁=1,公差d>0，且第二项，第五项，第十四项分别是等比数列{b_n}的第二项，第三项，第四项．

　 （1）求数列{a_n}与{b_n}的通项公式；

　 （2）设数列{c_n}对任意自然数n，均有，

求c₁+c₂+c₃+……+c₂₀₀₆值．

 

 

 

 

参考答案

题号	1	2	3	4	5	6	7	8	9	10	11
答案	D	D	A	B	C	D	C	B	A	B	A

12、3．2^n-1 13、510　　

 14、n（n+1）+1-2ⁿ15、4n+2　　16、4951

17、d=，n=50

18、解：由已知，得

　　　　　　　

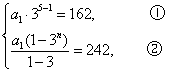
　　 由①得，解得 ．将代入②得　　　　　　　　　　　　　　　　　　　　　　　　 　，即　 ，解得　n＝5．∴ 数列的首项，项数n＝5．

　19、解析：(1)、由 ∴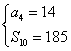　　　　　

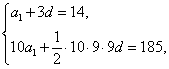
　(2)、设新数列为{}，由已知，　

20．解 设从2002年起，每年平均需新增住房面积为x万m²，则由题设可得下列不等式

解得.

答 设从2002年起，每年平均需新增住房面积为605万m².

21、解：（1）由题意得（a₁+d）(a₁+13d)=(a₁+4d)²(d>0)　解得d=2,∴a_n=2n-1,b_n=3^n-1.

　（2）当n=1时，c₁=3 当n≥2时， ，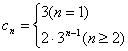