高二数学《必修5》综合训练
高二( )班 学号 姓名
一、选择题(每题4分,共40分)
1、在等差数列{an}中,a5=33,a45=153,则201是该数列的第( )项
A.60
B.
2、在100和500之间能被9整除的所有数之和为( )
A.12699
B.
3、等比数列{an}中,a3,a9是方程3x2—11x+9=0的两个根,则a6=( )
A.3 B.![]() C.± D.以上皆非
C.± D.以上皆非
4、四个不相等的正数a,b,c,d成等差数列,则( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积等于( )
的面积等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、在![]() 中,a,b,c分别是
中,a,b,c分别是![]() 所对应的边,
所对应的边,![]() ,则
,则![]() 的取值范围是( ) A.(1,2) B.
的取值范围是( ) A.(1,2) B.![]() C.
C.![]() D.
D.![]()
7、不等式![]() 的解集是(
)
的解集是(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、关于x的方程ax2+2x-1=0至少有一个正的实根,则a的取值范围是( )
A.a≥0 B.-1≤a<
9、在坐标平面上,不等式组![]() 所表示的平面区域的面积为( )
所表示的平面区域的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.2
D.2
10、已知点P(x,y)在不等式组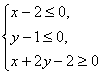 表示的平面区域上运动,则z=x-y的取值范围是( )
表示的平面区域上运动,则z=x-y的取值范围是( )
A.[-2,-1] B.[-2,
二、 填空题(每题4分,共16分)
11、数列![]() 的前n项的和Sn=2n2-n+1,则an=
的前n项的和Sn=2n2-n+1,则an=
12、已知![]() 时,函数有最_______值是 .
时,函数有最_______值是 .
13、不等式![]() 的解集是_______________________________
的解集是_______________________________
14、在下列函数中,
①![]() ;②
;②![]() ;③
;③![]() ;
;
④![]() ;⑤
;⑤![]() ;⑥
;⑥![]() ;⑦
;⑦![]() ;⑧
;⑧![]() ;其中最小值为2的函数是
(填入正确命题的序号)
;其中最小值为2的函数是
(填入正确命题的序号)
三、解答题
15、(6分)在等比数列![]() 中,
中,![]() ,
,![]()
试求:(I)![]() 和公比
和公比![]() ;(II)前6项的和
;(II)前6项的和![]() .
.
16、(6分)解关于x的不等式![]()
![]()
17、(8分)已知![]() 、
、![]() 、
、![]() 分别是
分别是![]() 的三个内角
的三个内角![]() 、
、![]() 、
、![]() 所对的边
所对的边
【Ⅰ】若![]() 面积
面积![]() 求
求![]() 、
、![]() 的值;
的值;
【Ⅱ】若![]() ,且
,且![]() ,试判断
,试判断![]() 的形状.
的形状.
18、(8分)某工厂用7万元钱购买了一台新机器,运输安装费用2千元,每年投保、动力消耗的费用也为2千元,每年的保养、维修、更换易损零件的费用逐年增加,第一年为2千元,第二年为3千元,第三年为4千元,依此类推,即每年增加1千元.问这台机器最佳使用年限是多少年?并求出年平均费用的最小值.
 19、(8分)某村计划建造一个室内面积为800
19、(8分)某村计划建造一个室内面积为800![]() 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1![]() 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3![]() 宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大?最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大?最大种植面积是多少?
20、(8分)某厂使用两种零件A、B装配两种产品P、Q,该厂的生产能力是月产P产品最多有2500件,月产Q产品最多有1200件;而且组装一件P产品要4个A、2个B,组装一件Q产品要6个A、8个B,该厂在某个月能用的A零件最多14000个;B零件最多12000个。已知P产品每件利润1000元,Q产品每件2000元,欲使月利润最大,需要组装P、Q产品各多少件?最大利润多少万元?
答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | B | B | C | A | B | C | B | D | B | C |
二、填空题
11、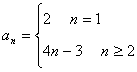 ; 12、5; 大;-6
; 12、5; 大;-6
13、![]() ; 14、①②④⑤⑦
; 14、①②④⑤⑦
三、解答题
15、解:(I)在等比数列![]() 中,由已知可得:
中,由已知可得:
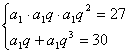 ………………………………………….2分
………………………………………….2分
解得:![]() 或
或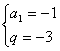 ……………………………………………….4分
……………………………………………….4分
(II)![]()
![]() 当
当![]() 时,
时, ![]() .……………..…… 5分
.……………..…… 5分
当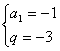 时,
时,![]() …….…….6分
…….…….6分
16、原不等式![]()
![]() . 分情况讨论
. 分情况讨论
(i)当![]() 时,不等式的解集为
时,不等式的解集为![]() ;………………….2分
;………………….2分
(ii)当![]() 时,不等式的解集为
时,不等式的解集为![]() ……………….4分
……………….4分
(iii)当![]() 时,不等式的解集为
时,不等式的解集为![]() ;………………….6分
;………………….6分
17、解:【Ⅰ】![]() ,
,![]() ,得
,得![]() … ……2分
… ……2分
由余弦定理得:![]() ,
,
所以![]() …………4分
…………4分
【Ⅱ】由余弦定理得:![]() ,
,
所以![]() …………6分
…………6分
在![]() 中,
中,![]() ,所以
,所以![]() …………7分
…………7分
所以![]() 是等腰直角三角形;…………8分
是等腰直角三角形;…………8分
18、[解析]设这台机器最佳使用年限是n年,则n年的保养、维修、更换易损零件的总费用为:
![]()
![]() ,
,
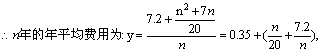 …………4分
…………4分
![]() …………6分
…………6分
等号当且仅当![]()
![]()
答:这台机器最佳使用年限是12年,年平均费用的最小值为1.55万元.…………8分
19、解:设矩形温室的左侧边长为a m,后侧边长为b m,则 ab=800.
蔬菜的种植面积 ![]() …………4分
…………4分
所以 ![]() …………6分
…………6分
当且仅当![]()
答:当矩形温室的左侧边长为
 20、解:设分别生产P、Q产品x件、y件,则有
20、解:设分别生产P、Q产品x件、y件,则有

设利润 z=1000x+2000y=1000(x+2y) …………3分
要使利润最大,只需求z的最大值.
作出可行域如图示(阴影部分及边界)
作出直线l:1000(x+2y)=0,即x+2y=0 …………6分
由于向上平移平移直线l时,z的值增大,所以在点A处z取得最大值
由![]() 解得
解得![]() ,即A(2000,1000) …………7分
,即A(2000,1000) …………7分
因此,此时最大利润zmax=1000(x+2y)==400(万元). …………8分
答:要使月利润最大,需要组装P、Q产品2000件、1000件,此时最大利润为400万元。