高二数学期中复习检测题2
班级 姓名
一.选择题
1、数列![]() 的通项为
的通项为![]() =
=![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() ,则使
,则使![]() >48成立的
>48成立的![]() 的最小值为A.7 B.
的最小值为A.7 B.
2、若不等式![]() 和不等式
和不等式![]() 的解集相同,则
的解集相同,则![]() 、
、![]() 的值为( )
的值为( )
A.![]() =﹣8
=﹣8 ![]() =﹣10 B.
=﹣10 B.![]() =﹣4
=﹣4 ![]() =﹣
=﹣![]() =﹣1
=﹣1 ![]() =9 D.
=9 D.![]() =﹣1
=﹣1 ![]() =2
=2
3、△ABC中,若![]() ,则△ABC的形状为
( )
,则△ABC的形状为
( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.锐角三角形
4、在首项为21,公比为![]() 的等比数列中,最接近1的项是
( )
的等比数列中,最接近1的项是
( )
A.第三项 B.第四项 C.第五项 D.第六项
( )
5、某厂去年的产值记为1,计划在今后五年内每年的产值比上年增长![]() ,则从今年起到第五年,这个厂的总产值为
( )
,则从今年起到第五年,这个厂的总产值为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
6.满足![]() 的△ABC的个数为m,则am的值为 ( )
的△ABC的个数为m,则am的值为 ( )
A.4 B.
7.在各项都为正数的等比数列![]() 中,a1=3,前三项和为21,则a3 + a4 + a5
=( )
中,a1=3,前三项和为21,则a3 + a4 + a5
=( )
A.33 B.
8.在△ABC 中,若a、b、c成等比数例,且c =
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.正数a、b的等差中项是![]() ,且
,且![]() 的最小值是( )
的最小值是( )
A.3 B.
10. 在3和9之间插入两个正数,使前三个数成等比数列,后三个数成等差数列,则插入的这两个正数之和为A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() ( )
( )
11. 等差数列![]() 中,
中,![]() 则使前
则使前![]() 项和
项和![]() 成立的最大自然数
成立的最大自然数![]() 为A. 4005 B.
为A. 4005 B.
12. 已知数列![]() 的前
的前![]() 项和为
项和为![]() ,则
,则
![]() 的值是A.
的值是A. ![]() B.
B.
二.填空题
13.写出命题:“至少有一个实数![]() ,使
,使![]() =
=
14.数列![]() 的前
的前![]() 项和
项和![]() ,则
,则![]()
15、设变量![]() 、
、![]() 满足约束条件
满足约束条件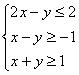 ,则
,则![]() 的最大值为
的最大值为
16、《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给五人,使每人成等差数列,且使最大的三份之和的![]() 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是
 17.已知数列
17.已知数列![]() 是首项为1,公差为2的等差数列,将数列
是首项为1,公差为2的等差数列,将数列![]() 中的各项排成如右一个三角形数表:
记A(i,j)表示第i行从左至右的第j个数,例如,A(4,3)=a9=17.
则A(10,2) .(用数字作答)
中的各项排成如右一个三角形数表:
记A(i,j)表示第i行从左至右的第j个数,例如,A(4,3)=a9=17.
则A(10,2) .(用数字作答)
18.已知x>1,则3x+![]() +1的最小值为
;
+1的最小值为
;
19. 在等差数列![]() 中, 若
中, 若![]() 则有等式
则有等式![]() 成立
成立![]() . 类比上述性质, 相应地, 在等比数列
. 类比上述性质, 相应地, 在等比数列![]() 中, 若
中, 若![]() ,则有等式
________成立.
,则有等式
________成立.
20. 在等差数列![]() 中,
中, ![]() , 且
, 且![]() ,
, ![]() 为其前
为其前![]() 项和,则
项和,则![]() 取最大值时,
取最大值时, ![]() 的值是
的值是
三.解答题
21.已知![]() ,且
,且![]() (A∩CRB).求实数a的取值范围.
(A∩CRB).求实数a的取值范围.
22.解下列关于x的不等式 ![]()
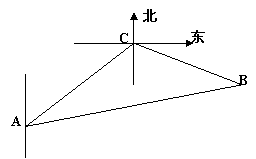 23. 一缉私艇发现在北偏东
23. 一缉私艇发现在北偏东![]() 方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南
方向,距离12 nmile的海面上有一走私船正以10 nmile/h的速度沿东偏南![]() 方向逃窜.缉私艇的速度为14
nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
方向逃窜.缉私艇的速度为14
nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东![]() 的方向去追,.求追及所需的时间和
的方向去追,.求追及所需的时间和![]() 角的正弦值.
角的正弦值.
24、△ABC中,![]() 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且![]()
(1)求∠B的大小;
(2)若![]() =4,
=4,![]() ,求
,求![]() 的值。
的值。
25.数列{an}中,a1=8,a4=2且满足an+2=2an+1-an ![]()
(Ⅰ)求数列{an}的通项公式;(Ⅱ)设Sn=a1+a2+…+an,求Sn;
(Ⅲ)设bn= ![]() ,Tn=b1+b2+…+bn
,Tn=b1+b2+…+bn![]() ,是否存在最大
,是否存在最大
的整数m,使得对任意n∈N,均有Tn>成立?若存在,求出m的值;若不存在,请说明理由.
26.设数列{an}的前n项为Sn,点![]() 均在函数y = 3x-2的图象上.
均在函数y = 3x-2的图象上.
(1)求数列{an}的通项公式。
(2)设![]() ,Tn为数列{bn}的前n项和,求使得
,Tn为数列{bn}的前n项和,求使得![]() 对所有
对所有![]() 都成立的最小正整数m.
都成立的最小正整数m.
27、设不等式组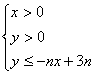 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为![]()
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)记![]() ,试比较
,试比较![]() 的大小;若对于一切的正整数
的大小;若对于一切的正整数![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() 为数列
为数列![]() 的前
的前![]() 项的和,其中
项的和,其中![]() ,问是否存在正整数
,问是否存在正整数![]() ,使
,使![]() 成立?若存在,求出正整数
成立?若存在,求出正整数![]() ;若不存在
;若不存在
一.选择题
1.B; 2.B; 3.B; 4.C; 5.D; 6.A 7.C 8.B 9.C 10.B 11.B12.A
二.填空题
13.![]() 14. 48 16.18; 17.10;
14. 48 16.18; 17.10;
18.在分式的位置凑出分母x-1,在3x后面施加互逆运算:±3
原式=(3x-3)+3+![]() +1=3(x-1)+
+1=3(x-1)+![]() +4≥2
+4≥2![]() =4
=4![]() +4
+4
19. ![]() (
(![]() )
)
20.解: 由题意得 ![]() ,
,
![]()
![]() 时,
时,![]() 有最大值.
有最大值.
三.解答题
21.解:A = {xx2-x-6<0} = {x-2 < x < 3}
B = {xx2 + 2x-8≥0} = {x≤-4或x≥2}………………………………… 2分
|
∴ ={x-4< x <2}
|
A∩ = {x-2 < x < 2} ………………………………………… 4分
又![]()
![]()
∴当a > 0时,C = {x a < x < 3a}
|
∵![]() (A∩ )
(A∩ )
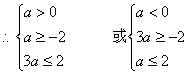 ……………………………………………8分
……………………………………………8分
![]() ……………………………………………10分
……………………………………………10分
22解:方程![]() 的两根为-m<
的两根为-m<
①当-m<![]() 或m>0时,原不等式的解集为
或m>0时,原不等式的解集为![]() ;
;
②当-m=![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
③当-m>![]() <m<0时,原不等式的解集为
<m<0时,原不等式的解集为![]() ;
;
23. (本小题14分)
解: 设A,C分别表示缉私艇,走私船的位置,设经过 ![]() 小时后在B处追上, 则有
小时后在B处追上, 则有
![]() ,
,
![]()
所以所需时间2小时,
![]()
24、⑴由![]()
![]()
![]()
![]()
![]()
⑵![]()
![]()
25.(Ⅰ)由an+2=2an+1-an Þ
an+2-an+1=an+1-an,可知{an}成等差数列,d==-2
∴an=10-2n.
(Ⅱ)由an=10-2n≥0得n≤5 ∴当n≤5时,Sn=-n2+9n,
当n>5时,Sn=n2-9n+40,
故Sn= ![]()
(Ⅲ)bn===()
∴Tn= b1+b2+…+bn
=[(1-)+(-)+(-)+……+(-)]
=(1-)=>>Tn-1>Tn-2>……>T1.
∴要使Tn>总成立,需<T1=恒成立,即m<8,(m∈Z).
故适合条件的m的最大值为7.
26.解:(1)∵点![]() 在函数y = 3x-2的图象上,
在函数y = 3x-2的图象上,
![]() ……………………………………3分
……………………………………3分
∴a1= s1 =1
当![]()
![]() ………………………………………… 6分
………………………………………… 6分
(2)![]() …………8分
…………8分
![]()
![]()
![]()
因此,使得![]() 成立的m必须且仅需满足
成立的m必须且仅需满足![]() ,故满足要求的最小整数m为10.……………………12分
,故满足要求的最小整数m为10.……………………12分
27、⑴![]()
当![]() 时,
时,![]() 取值为1,2,3,…,
取值为1,2,3,…,![]() 共有
共有![]() 个格点
个格点
当![]() 时,
时,![]() 取值为1,2,3,…,
取值为1,2,3,…,![]() 共有
共有![]() 个格点
个格点
∴![]()
⑵![]()
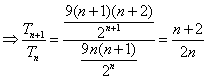
当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() 时,
时,![]()
![]() 时,
时,![]()
![]() 时,
时,![]()
∴![]() 中的最大值为
中的最大值为![]()
要使![]() 对于一切的正整数
对于一切的正整数![]() 恒成立,只需
恒成立,只需![]() ∴
∴![]()
⑶![]()
将![]() 代入
代入![]() ,化简得,
,化简得,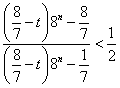 (﹡)
(﹡)
若![]() 时
时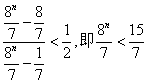 ,显然
,显然![]()
若![]() 时
时![]() (﹡)式化简为
(﹡)式化简为![]() 不可能成立
不可能成立
综上,存在正整数![]() 使
使![]() 成立.
成立.