典型例题一
例1 指出抛物线的焦点坐标、准线方程.
(1)![]() (2)
(2)![]()
分析:(1)先根据抛物线方程确定抛物线是四种中哪一种,求出p,再写出焦点坐标和准线方程.
(2)先把方程化为标准方程形式,再对a进行讨论,确定是哪一种后,求p及焦点坐标与准线方程.
解:(1)![]() ,∴焦点坐标是(0,1),准线方程是:
,∴焦点坐标是(0,1),准线方程是:![]()
(2)原抛物线方程为:![]() ,
,![]()
①当![]() 时,
时,![]() ,抛物线开口向右,
,抛物线开口向右,
∴焦点坐标是![]() ,准线方程是:
,准线方程是:![]() .
.
②当![]() 时,
时,![]() ,抛物线开口向左,
,抛物线开口向左,
∴焦点坐标是![]() ,准线方程是:
,准线方程是:![]() .
.
综合上述,当![]() 时,抛物线
时,抛物线![]() 的焦点坐标为
的焦点坐标为![]() ,准线方程是:
,准线方程是:![]() .
.
典型例题二
例2 若直线![]() 与抛物线
与抛物线![]() 交于A、B两点,且AB中点的横坐标为2,求此直线方程.
交于A、B两点,且AB中点的横坐标为2,求此直线方程.
分析:由直线与抛物线相交利用韦达定理列出k的方程求解.另由于已知与直线斜率及弦中点坐标有关,故也可利用“作差法”求k.
解法一:设![]() 、
、![]() ,则由:
,则由: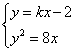 可得:
可得:![]() .
.
∵直线与抛物线相交,![]() 且
且![]() ,则
,则![]() .
.
∵AB中点横坐标为:![]() ,
,
解得:![]() 或
或![]() (舍去).
(舍去).
故所求直线方程为:![]() .
.
解法二:设![]() 、
、![]() ,则有
,则有![]() .
.
两式作差解:![]() ,即
,即![]() .
.
![]()
![]() ,
,
![]() 故
故![]() 或
或![]() (舍去).
(舍去).
则所求直线方程为:![]() .
.
典型例题三
例3 求证:以抛物线的焦点弦为直径的圆心与抛物线的准线相切.
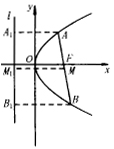 分析:可设抛物线方程为
分析:可设抛物线方程为![]() .如图所示,只须证明
.如图所示,只须证明![]() ,则以AB为直径的圆,必与抛物线准线相切.
,则以AB为直径的圆,必与抛物线准线相切.
证明:作![]() 于
于![]() 于
于![]() .M为AB中点,作
.M为AB中点,作![]() 于
于![]() ,则由抛物线的定义可知:
,则由抛物线的定义可知:![]()
在直角梯形![]() 中:
中:
![]()
![]() ,故以AB为直径的圆,必与抛物线的准线相切.
,故以AB为直径的圆,必与抛物线的准线相切.
说明:类似有:以椭圆焦点弦为直径的圆与相对应的准线相离,以双曲线焦点弦为直径的圆与相应的准线相交.
典型例题四
例4(1)设抛物线![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() ,求k值.
,求k值.
(2)以(1)中的弦为底边,以x轴上的点P为顶点作三角形,当三角形的面积为9时,求P点坐标.
分析:(1)题可利用弦长公式求k,(2)题可利用面积求高,再用点到直线距离求P点坐标.
解:(1)由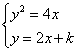 得:
得:![]()
设直线与抛物线交于![]() 与
与![]() 两点.则有:
两点.则有:![]()
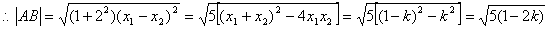
![]() ,即
,即![]()
(2)![]() ,底边长为
,底边长为![]() ,∴三角形高
,∴三角形高![]()
∵点P在x轴上,∴设P点坐标是![]()
则点P到直线![]() 的距离就等于h,即
的距离就等于h,即![]()
![]() 或
或![]() ,即所求P点坐标是(-1,0)或(5,0).
,即所求P点坐标是(-1,0)或(5,0).
典型例题五
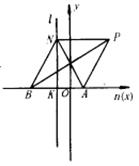
例5 已知定直线l及定点A(A不在l上),n为过A且垂直于l的直线,设N为l上任一点,AN的垂直平分线交n于B,点B关于AN的对称点为P,求证P的轨迹为抛物线.
分析:要证P的轨迹为抛物线,有两个途径,一个证明P点的轨迹符合抛物线的定义,二是证明P的轨迹方程为抛物线的方程,可先用第一种方法,由A为定点,l为定直线,为我们提供了利用定义的信息,若能证明![]() 且
且![]() 即可.
即可.
证明:如图所示,连结PA、PN、NB.
由已知条件可知:PB垂直平分NA,且B关于AN的对称点为P.
∴AN也垂直平分PB.则四边形PABN为菱形.即有![]() .
.
![]()
则P点符合抛物线上点的条件:到定点A的距离与到定直线的距离相等,所以P点的轨迹为抛物线.
典型例题六
例6 若线段![]() 为抛物线
为抛物线![]() 的一条焦点弦,F为C的焦点,求证:
的一条焦点弦,F为C的焦点,求证:![]() .
.
分析:此题证的是距离问题,如果把它们用两点间的距离表示出来,其计算量是很大的.我们可以用抛物线的定义,巧妙运用韦达定理,也可以用抛物线的定义与平面几何知识,把结论证明出来.
证法一:![]() ,若过F的直线即线段
,若过F的直线即线段![]() 所在直线斜率不存在时,
所在直线斜率不存在时,
则有![]() ,
,![]() .
.
若线段![]() 所在直线斜率存在时,设为k,则此直线为:
所在直线斜率存在时,设为k,则此直线为:![]() ,且设
,且设![]() .
.
由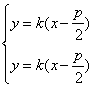 得:
得:![]()
![]() ①
①
![]() ②
②
根据抛物线定义有:![]()
则![]()
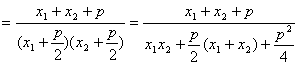
请将①②代入并化简得:![]()
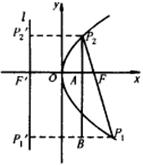 证法二:如图所示,设
证法二:如图所示,设![]() 、
、![]() 、F点在C的准线l上的射影分别是
、F点在C的准线l上的射影分别是![]() 、
、![]() 、
、![]() ,且不妨设
,且不妨设![]() ,又设
,又设![]() 点在
点在![]() 、
、![]() 上的射影分别是A、B点,由抛物线定义知,
上的射影分别是A、B点,由抛物线定义知,
![]()
又![]() ∽
∽![]() ,
,![]()
即![]()
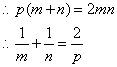
故原命题成立.
典型例题七
例7 设抛物线方程为![]() ,过焦点F的弦AB的倾斜角为
,过焦点F的弦AB的倾斜角为![]() ,求证:焦点弦长为
,求证:焦点弦长为![]() .
.
分析:此题做法跟上题类似,也可采用韦达定理与抛物线定义解决问题.
证法一:抛物线![]() 的焦点为
的焦点为![]() ,
,
过焦点的弦AB所在的直线方程为:![]()
由方程组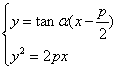 消去y得:
消去y得:
![]()
设![]() ,则
,则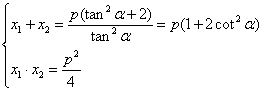
又![]()
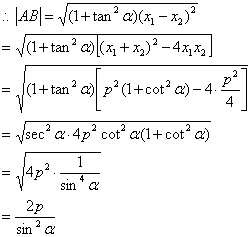
即![]()
证法二:如图所示,分别作![]() 、
、![]() 垂直于准线l.由抛物线定义有:
垂直于准线l.由抛物线定义有:
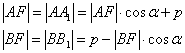
 于是可得出:
于是可得出:![]()
![]()
故原命题成立.
典型例题八
例8 已知圆锥曲线C经过定点![]() ,它的一个焦点为F(1,0),对应于该焦点的准线为
,它的一个焦点为F(1,0),对应于该焦点的准线为![]() ,过焦点F任意作曲线C的弦AB,若弦AB的长度不超过8,且直线AB与椭圆
,过焦点F任意作曲线C的弦AB,若弦AB的长度不超过8,且直线AB与椭圆![]() 相交于不同的两点,求
相交于不同的两点,求
(1)AB的倾斜角![]() 的取值范围.
的取值范围.
(2)设直线AB与椭圆相交于C、D两点,求CD中点M的轨迹方程.
分析:由已知条件可确定出圆锥曲线C为抛物线,AB为抛物线的焦点弦,设其斜率为k,弦AB与椭圆相交于不同的两点,可求出k的取值范围,从而可得![]() 的取值范围,求CD中点M的轨迹方程时,可设出M的坐标,利用韦达定理化简即可.
的取值范围,求CD中点M的轨迹方程时,可设出M的坐标,利用韦达定理化简即可.
解:(1)由已知得![]() .故P到
.故P到![]() 的距离
的距离![]() ,从而
,从而![]()
∴曲线C是抛物线,其方程为![]() .
.
设直线AB的斜率为k,若k不存在,则直线AB与![]() 无交点.
无交点.
∴k存在.设AB的方程为![]()
由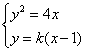 可得:
可得:![]()
设A、B坐标分别为![]() 、
、![]() ,则:
,则:![]()
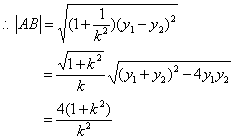
∵弦AB的长度不超过8,![]() 即
即![]()
由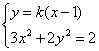 得:
得:![]()
∵AB与椭圆相交于不同的两点,![]()
由![]() 和
和![]() 可得:
可得:![]() 或
或![]()
故![]() 或
或![]()
又![]() ,∴所求
,∴所求![]() 的取值范围是:
的取值范围是:![]() 或
或![]()
(2)设CD中点![]() 、
、![]() 、
、![]()
由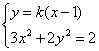 得:
得:![]()
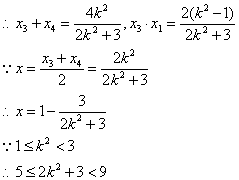
则![]() 即
即![]() .
.
化简得:![]()
∴所求轨迹方程为:![]()
典型例题九
例9 定长为3的线段![]() 的端点
的端点![]() 、
、![]() 在抛物线
在抛物线![]() 上移动,求
上移动,求![]() 的中点到
的中点到![]() 轴的距离的最小值,并求出此时
轴的距离的最小值,并求出此时![]() 中点的坐标.
中点的坐标.
分析:线段![]() 中点到
中点到![]() 轴距离的最小值,就是其横坐标的最小值.这是中点坐标问题,因此只要研究
轴距离的最小值,就是其横坐标的最小值.这是中点坐标问题,因此只要研究![]() 、
、![]() 两点的横坐标之和取什么最小值即可.
两点的横坐标之和取什么最小值即可.
解:如图,设![]() 是
是![]() 的焦点,
的焦点,![]() 、
、![]() 两点到准线的垂线分别是
两点到准线的垂线分别是![]() 、
、![]() ,又
,又![]() 到准线的垂线为
到准线的垂线为![]() ,
,![]() 、
、![]() 和
和![]() 是垂足,则
是垂足,则
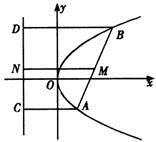
![]() .
.
设![]() 点的横坐标为
点的横坐标为![]() ,纵坐标为
,纵坐标为![]() ,
,![]() ,则
,则![]() .
.
等式成立的条件是![]() 过点
过点![]() .
.
当![]() 时,
时,![]() ,故
,故
![]() ,
,
![]() ,
,![]() .
.
所以![]() ,此时
,此时![]() 到
到![]() 轴的距离的最小值为
轴的距离的最小值为![]() .
.
说明:本题从分析图形性质出发,把三角形的性质应用到解析几何中,解法较简.
典型例题十
例10 过抛物线![]() 的焦点
的焦点![]() 作倾斜角为
作倾斜角为![]() 的直线,交抛物线于
的直线,交抛物线于![]() 、
、![]() 两点,求
两点,求![]() 的最小值.
的最小值.
分析:本题可分![]() 和
和![]() 两种情况讨论.当
两种情况讨论.当![]() 时,先写出
时,先写出![]() 的表达式,再求范围.
的表达式,再求范围.
解:(1)若![]() ,此时
,此时![]() .
.
(2)若![]() ,因有两交点,所以
,因有两交点,所以![]() .
.
![]() ,即
,即![]() .
.
代入抛物线方程,有![]() .
.
故![]() ,
,
![]() .
.
故![]() .
.
所以![]() .因
.因![]() ,所以这里不能取“=”.
,所以这里不能取“=”.
综合(1)(2),当![]() 时,
时,![]() .
.
说明:
(1)此题须对![]() 分
分![]() 和
和![]() 两种情况进行讨论;
两种情况进行讨论;
(2)从解题过程可知,抛物线点弦长公式为![]() ;
;
(3)当![]() 时,
时,![]() 叫做抛物线的通径.通径是最短的焦点弦.
叫做抛物线的通径.通径是最短的焦点弦.
典型例题十一
例11 过抛物线![]()
![]() 的焦点
的焦点![]() 作弦
作弦![]() ,
,![]() 为准线,过
为准线,过![]() 、
、![]() 作
作![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() 、
、![]() ,则①
,则①![]() 为( ),②
为( ),②![]() 为( ).
为( ).
A.大于等于![]() B.小于等于
B.小于等于![]() C.等于
C.等于![]() D不确定
D不确定
分析:本题考查抛物线的定义、直线与圆的位置关系等方面的知识,关键是求角的大小以及判定直线与圆是否相切.
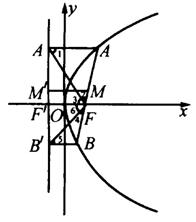
解:①点![]() 在抛物线上,由抛物线定义,则
在抛物线上,由抛物线定义,则![]() ,
,
又![]() 轴
轴![]() .
.
∴![]() ,同理
,同理![]() ,
,
而![]() ,∴
,∴![]() ,
,
∴![]() .选C.
.选C.
②过![]() 中点
中点![]() 作
作![]() ,垂中为
,垂中为![]() ,
,
则![]() .
.
∴以![]() 为直径的圆与直线
为直径的圆与直线![]() 相切,切点为
相切,切点为![]() .
.
又![]() 在圆的外部,∴
在圆的外部,∴![]() .
.
特别地,当![]() 轴时,
轴时,![]() 与
与![]() 重合,
重合,![]() .
.
即![]() ,选B.
,选B.
典型例题十二
例12 已知点![]() ,
,![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在该抛物线上移动,当
在该抛物线上移动,当![]() 取最小值时,点
取最小值时,点![]() 的坐标为__________.
的坐标为__________.
分析:本题若建立目标函数来求![]() 的最小值是困难的,若巧妙地利用抛物线定义,结合图形则问题不难解决.
的最小值是困难的,若巧妙地利用抛物线定义,结合图形则问题不难解决.
解:如图,
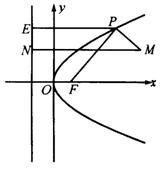
由定义知![]() ,故
,故![]() .
.
取等号时,![]() 、
、![]() 、
、![]() 三点共线,∴
三点共线,∴![]() 点纵坐标为2,代入方程,求出其横坐标为2,
点纵坐标为2,代入方程,求出其横坐标为2,
所以![]() 点坐标为
点坐标为![]() .
.
说明:由抛物线的定义可知,抛物线上的点到焦点的距离等于它到准线的距离.要重视定义在解题中的应用,灵活地进行抛物线上的点到焦点距离与到准线距离的相互转换.