典型例题一
例1 过抛物线焦点的一条直线与它交于两点P、Q,通过点P和抛物线顶点的直线交准线于点M,如何证明直线MQ平行于抛物线的对称轴?
解:思路一:求出M、Q的纵坐标并进行比较,如果相等,则MQ//x轴,为此,将方程![]() 联立,解出
联立,解出
![]()
![]()
直线OP的方程为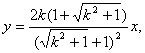 即
即![]()
令![]() ,得M点纵坐标
,得M点纵坐标![]() 得证.
得证.
由此可见,按这一思路去证,运算较为繁琐.
思路二:利用命题“如果过抛物线![]() 的焦点的一条直线和这条抛物线相交,两上交点的纵坐标为
的焦点的一条直线和这条抛物线相交,两上交点的纵坐标为![]() 、
、![]() ,那么
,那么![]() ”来证.
”来证.
设![]() 、
、![]() 、
、![]() ,并从
,并从![]() 及
及![]() 中消去x,得到
中消去x,得到![]() ,则有结论
,则有结论![]() ,即
,即![]() .
.
又直线OP的方程为![]() ,
, ![]() ,得
,得![]() .
.
因为![]() 在抛物线上,所以
在抛物线上,所以![]() .
.
从而![]() .
.
这一证法运算较小.
思路三:直线MQ的方程为![]() 的充要条件是
的充要条件是![]() .
.
将直线MO的方程![]() 和直线QF的方程
和直线QF的方程![]() 联立,它的解(x ,y)就是点P的坐标,消去
联立,它的解(x ,y)就是点P的坐标,消去![]() 的充要条件是点P在抛物线上,得证.这一证法巧用了充要条件来进行逆向思维,运算量也较小.
的充要条件是点P在抛物线上,得证.这一证法巧用了充要条件来进行逆向思维,运算量也较小.
说明:本题中过抛物线焦点的直线与x轴垂直时(即斜率不存在),容易证明成立.
典型例题二
例2 已知过抛物线![]() 的焦点且斜率为1的直线交抛物线于A、B两点,点R是含抛物线顶点O的弧AB上一点,求△RAB的最大面积.
的焦点且斜率为1的直线交抛物线于A、B两点,点R是含抛物线顶点O的弧AB上一点,求△RAB的最大面积.
分析:求RAB的最大面积,因过焦点且斜率为1的弦长为定值,故可以![]() 为三角形的底,只要确定高的最大值即可.
为三角形的底,只要确定高的最大值即可.
解:设AB所在的直线方程为![]() .
.
将其代入抛物线方程![]() ,消去x得
,消去x得![]()
![]()
当过R的直线l平行于AB且与抛物线相切时,△RAB的面积有最大值.
设直线l方程为![]() .代入抛物线方程得
.代入抛物线方程得![]()
由![]() 得
得![]() ,这时
,这时![]() .它到AB的距离为
.它到AB的距离为![]()
∴△RAB的最大面积为![]() .
.
典型例题三
例3 直线![]() 过点
过点![]() ,与抛物线
,与抛物线![]() 交于
交于![]() 、
、![]() 两点,P是线段
两点,P是线段![]()
![]() 的中点,直线
的中点,直线![]() 过P和抛物线的焦点F,设直线
过P和抛物线的焦点F,设直线![]() 的斜率为k.
的斜率为k.
(1)将直线![]() 的斜率与直线
的斜率与直线![]() 的斜率之比表示为k的函数
的斜率之比表示为k的函数![]() ;
;
(2)求出![]() 的定义域及单调区间.
的定义域及单调区间.
分析:![]() 过点P及F,利用两点的斜率公式,可将
过点P及F,利用两点的斜率公式,可将![]() 的斜率用k表示出来,从而写出
的斜率用k表示出来,从而写出![]() ,由函数
,由函数![]() 的特点求得其定义域及单调区间.
的特点求得其定义域及单调区间.
解:(1)设![]() 的方程为:
的方程为:![]() ,将它代入方程
,将它代入方程![]() ,得
,得
![]()
设![]() ,则
,则![]()
将![]() 代入
代入![]() 得:
得:![]() ,即P点坐标为
,即P点坐标为![]() .
.
由![]() ,知焦点
,知焦点![]() ,∴直线
,∴直线![]() 的斜率
的斜率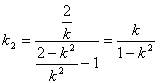
∴函数![]() .
.
(2)∵![]() 与抛物线有两上交点,∴
与抛物线有两上交点,∴![]() 且
且![]()
解得![]() 或
或![]()
∴函数![]() 的定义域为
的定义域为![]()
当![]() 时,
时,![]() 为增函数.
为增函数.
典型例题四
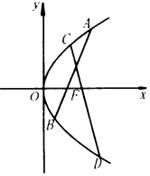 例4 如图所示:直线l过抛物线
例4 如图所示:直线l过抛物线![]() 的焦点,并且与这抛物线相交于A、B两点,求证:对于这抛物线的任何给定的一条弦CD,直线l不是CD的垂直平分线.
的焦点,并且与这抛物线相交于A、B两点,求证:对于这抛物线的任何给定的一条弦CD,直线l不是CD的垂直平分线.
分析:本题所要证的命题结论是否定形式,一方面可根据垂直且平分列方程得矛盾结论;别一方面也可以根据l上任一点到C、D距离相等来得矛盾结论.
证法一:假设直线l是抛物线的弦CD的垂直平方线,因为直线l与抛物线交于A、B两点,所以直线l的斜率存在,且不为零;直线CD的斜率存在,且不为0.
设C、D的坐标分别为![]() 与
与![]() .则
.则![]()
∴l的方程为![]()
∵直线l平分弦CD
∴CD的中点![]() 在直线l上,
在直线l上,
即![]() ,化简得:
,化简得:![]()
由![]() 知
知![]() 得到矛盾,所以直线l不可能是抛物线的弦CD的垂直平分线.
得到矛盾,所以直线l不可能是抛物线的弦CD的垂直平分线.
证法二:假设直线l是弦CD的垂直平分线
∵焦点F在直线l上,∴![]()
由抛物线定义,![]() 到抛物线的准线
到抛物线的准线![]() 的距离相等.
的距离相等.
∵![]() ,
,
∴CD的垂直平分线l:![]() 与直线l和抛物线有两上交点矛盾,下略.
与直线l和抛物线有两上交点矛盾,下略.
典型例题五
例5 设过抛物线![]() 的顶点O的两弦OA、OB互相垂直,求抛物线顶点O在AB上射影N的轨迹方程.
的顶点O的两弦OA、OB互相垂直,求抛物线顶点O在AB上射影N的轨迹方程.
分析:求与抛物线有关的轨迹方程,可先把N看成定点![]() ;待求得
;待求得![]() 的关系后再用动点坐标
的关系后再用动点坐标![]() 来表示,也可结合几何知识,通过巧妙替换,简化运算.
来表示,也可结合几何知识,通过巧妙替换,简化运算.
解法一:设![]()
则:![]() ,
,![]()
![]() ,
,![]() 即
即![]()
![]()
![]() ,
,![]() ①
①
把N点看作定点,则AB所在的直线方程为:![]() 显然
显然![]()
![]() 代入
代入![]() 化简整理得:
化简整理得:![]()
![]() ,
,![]() ②
②
由①、②得:![]() ,化简得
,化简得![]()
用x、y分别表示![]() 得:
得:![]()
解法二:点N在以OA、OB为直径的两圆的交点(非原点)的轨迹上,设![]() ,则以OA为直径的圆方程为:
,则以OA为直径的圆方程为:![]()
![]() ①
①
设![]() ,OA⊥OB,则
,OA⊥OB,则![]()
在求以OB为直径的圆方程时以![]() 代
代![]() ,可得
,可得
![]() ②
②
由①+②得:![]()
![]()
典型例题六
例6如图所示,直线![]() 和
和![]() 相交于点M,
相交于点M,![]() ⊥
⊥![]() ,点
,点![]() ,以A、B为端点的曲线段C上的任一点到
,以A、B为端点的曲线段C上的任一点到![]() 的距离与到点N的距离相等,若△AMN为锐角三角形,
的距离与到点N的距离相等,若△AMN为锐角三角形,![]() ,
,![]() ,且
,且![]() ,建立适当的坐标系,求曲线段C的方程.
,建立适当的坐标系,求曲线段C的方程.
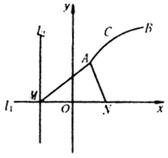 分析:因为曲线段C上的任一点是以点N为焦点,以
分析:因为曲线段C上的任一点是以点N为焦点,以![]() 为准线的抛物线的一段,所以本题关键是建立适当坐标系,确定C所满足的抛物线方程.
为准线的抛物线的一段,所以本题关键是建立适当坐标系,确定C所满足的抛物线方程.
解:以![]() 为x轴,MN的中点为坐标原点O,建立直角坐标系.
为x轴,MN的中点为坐标原点O,建立直角坐标系.
由题意,曲线段C是N为焦点,以![]() 为准线的抛物线的一段,其中A、B分别为曲线段的两端点.
为准线的抛物线的一段,其中A、B分别为曲线段的两端点.
∴设曲线段C满足的抛物线方程为:![]() 其中
其中![]() 、
、![]() 为A、B的横坐标
为A、B的横坐标
令![]() 则
则![]() ,
,![]()
∴由两点间的距离公式,得方程组: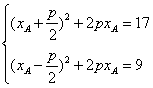
解得![]() 或
或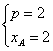
∵△AMN为锐角三角形,∴![]() ,则
,则![]() ,
,![]()
又B在曲线段C上,![]()
则曲线段C的方程为![]()
典型例题七
例7如图所示,设抛物线![]() 与圆
与圆![]() 在x轴上方的交点为A、B,与圆
在x轴上方的交点为A、B,与圆![]() 在x由上方的交点为C、D,P为AB中点,Q为CD的中点.(1)求
在x由上方的交点为C、D,P为AB中点,Q为CD的中点.(1)求![]() .(2)求△ABQ面积的最大值.
.(2)求△ABQ面积的最大值.
分析:由于P、Q均为弦AB、CD的中点,故可用韦达定理表示出P、Q两点坐标,由两点距离公式即可求出![]() .
.
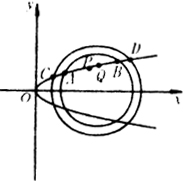 解:(1)设
解:(1)设![]()
由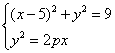 得:
得:![]() ,
,
![]()
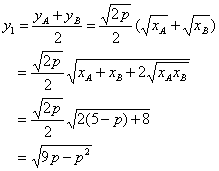
由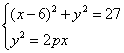 得
得![]() ,
,
![]()
![]()
同![]() 类似,
类似,![]()
则![]() ,
,![]()
(2)![]()
![]()
![]() ,∴当
,∴当![]() 时,
时,![]() 取最大值
取最大值![]() .
.
典型例题八
例8 已知直线![]() 过原点,抛物线
过原点,抛物线![]() 的顶点在原点,焦点在
的顶点在原点,焦点在![]() 轴的正半轴上,且点
轴的正半轴上,且点![]() 和点
和点![]() 关于直线
关于直线![]() 的对称点都在
的对称点都在![]() 上,求直线
上,求直线![]() 和抛物线
和抛物线![]() 的方程.
的方程.
分析:设出直线![]() 和抛物线
和抛物线![]() 的方程,由点
的方程,由点![]() 、
、![]() 关于直线
关于直线![]() 对称,求出对称点的坐标,分别代入抛物线方程.或设
对称,求出对称点的坐标,分别代入抛物线方程.或设![]() ,利用对称的几何性质和三角函数知识求解.
,利用对称的几何性质和三角函数知识求解.
解法一:设抛物线![]() 的方程为
的方程为![]()
![]() ,直线
,直线![]() 的方程为
的方程为![]()
![]() ,
,
则有点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() 、
、![]() ,
,
则有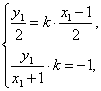 解得
解得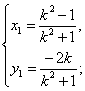
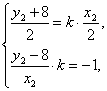 解得
解得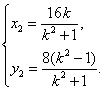
如图,![]() 、
、![]() 在抛物线上
在抛物线上
∴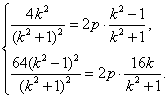
两式相除,消去![]() ,整理,得
,整理,得![]() ,故
,故![]() ,
,
由![]() ,
,![]() ,得
,得![]() .把
.把![]() 代入,得
代入,得![]() .
.
∴直线![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() .
.
解法二:设点![]() 、
、![]() 关于
关于![]() 的对称点为
的对称点为![]() 、
、![]() ,
,
又设![]() ,依题意,有
,依题意,有![]() ,
,![]() .
.
故![]() ,
,![]() .
.
由![]() ,知
,知![]() .
.
∴![]() ,
,![]() .
.
又![]() ,
,![]() ,故
,故![]() 为第一象限的角.
为第一象限的角.
∴![]() 、
、![]() .
.
将![]() 、
、![]() 的坐标代入抛物线方程,得
的坐标代入抛物线方程,得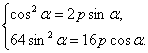
∴![]() ,即
,即![]() 从而
从而![]() ,
,![]() ,
,
∴![]() ,得抛物线
,得抛物线![]() 的方程为
的方程为![]() .
.
又直线![]() 平分
平分![]() ,得
,得![]() 的倾斜角为
的倾斜角为![]() .
.
∴![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
说明:
(1)本题属于点关于直线的对称问题.解法一是解对称点问题的基本方法,它的思路明确,但运算量大,若不仔细、沉着,难于解得正确结果.解法二是利用对称图形的性质来解,它的技巧性较强,一时难于想到.
(2)本题是用待定系数法求直线的方程和抛物线方程.在已知曲线的类型求曲线方程时,这种方法是最常规方法,需要重点掌握.
典型例题九
例9 如图,正方形![]() 的边
的边![]() 在直线
在直线![]() 上,
上,![]() 、
、![]() 两点在抛物线
两点在抛物线![]() 上,求正方形
上,求正方形![]() 的面积.
的面积.
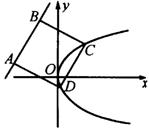
分析:本题考查抛物线的概念及其位置关系,方程和方程组的解法和数形结合的思想方法,以及分析问题、解决问题的能力.
解:∵直线![]() ,
,![]() ,∴设
,∴设![]() 的方程为
的方程为![]() ,且
,且![]() 、
、![]() .
.
由方程组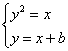 ,消去
,消去![]() ,得
,得![]() ,于是
,于是
![]() ,
,![]() ,∴
,∴![]() (其中
(其中![]() )
)
∴![]() .
.
由已知,![]() 为正方形,
为正方形,![]() ,
,
∴![]() 可视为平行直线
可视为平行直线![]() 与
与![]() 间的距离,则有
间的距离,则有
![]() ,于是得
,于是得![]() .
.
两边平方后,整理得,![]() ,∴
,∴![]() 或
或![]() .
.
当![]() 时,正方形
时,正方形![]() 的面积
的面积![]() .
.
当![]() 时,正方形
时,正方形![]() 的面积
的面积![]() .
.
∴正方形![]() 的面积为18或50.
的面积为18或50.
说明:运用方程(组)的思想和方法求某些几何量的值是解析几何中最基本的、贯穿始终的方法,本题应充分考虑正方形这一条件.
典型例题十
例10 设有一颗彗星围绕地球沿一抛物线轨道运行,地球恰好位于抛物线轨道的焦点处,当此彗星离地球为![]()
![]() 时,经过地球与彗星的直线与抛物线的轴的夹角为
时,经过地球与彗星的直线与抛物线的轴的夹角为![]() ,求这彗星与地球的最短距离.
,求这彗星与地球的最短距离.
分析:利用抛物线有关性质求解.
解:如图,设彗星轨道方程为![]() ,
,![]() ,焦点为
,焦点为![]() ,
,
彗星位于点![]() 处.直线
处.直线![]() 的方程为
的方程为![]() .
.
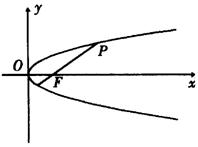
解方程组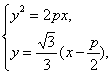 得
得![]() ,
,
故![]() .
.
![]() .
.
故![]() ,得
,得![]() .
.
由于顶点为抛物线上到焦点距离最近的点,所以顶点是抛物线上到焦点距离最近的点.焦点到抛物线顶点的距离为![]() ,所以彗星与地球的最短距离为
,所以彗星与地球的最短距离为![]()
![]() 或
或![]()
![]() ,(
,(![]() 点在
点在![]() 点的左边与右边时,所求距离取不同的值).
点的左边与右边时,所求距离取不同的值).
说明:
(1)此题结论有两个,不要漏解;
(2)本题用到抛物线一个重要结论:顶点为抛物线上的点到焦点距离最近的点,其证明如下:设![]() 为抛物线
为抛物线![]() 上一点,焦点为
上一点,焦点为![]() ,准线方程为
,准线方程为![]() ,依抛物线定义,有
,依抛物线定义,有![]()
![]() ,当
,当![]() 时,
时,![]() 最小,故抛物线上到焦点距离最近的点是抛物线的顶点.
最小,故抛物线上到焦点距离最近的点是抛物线的顶点.
典型例题十一
例11 如图,抛物线顶点在原点,圆![]() 的圆心是抛物线的焦点,直线
的圆心是抛物线的焦点,直线![]() 过抛物线的焦点,且斜率为2,直线
过抛物线的焦点,且斜率为2,直线![]() 交抛物线与圆依次为
交抛物线与圆依次为![]() 、
、![]() 、
、![]() 、
、![]() 四点,求
四点,求![]() 的值.
的值.
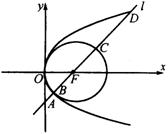
分析:本题考查抛物线的定义,圆的概念和性质,以及分析问题与解决问题的能力,本题的关键是把![]() 转化为直线被圆锥曲线所截得的弦长问题.
转化为直线被圆锥曲线所截得的弦长问题.
解:由圆的方程![]() ,即
,即![]() 可知,圆心为
可知,圆心为![]() ,半径为2,又由抛物线焦点为已知圆的圆心,得到抛物线焦点为
,半径为2,又由抛物线焦点为已知圆的圆心,得到抛物线焦点为![]() ,设抛物线方程为
,设抛物线方程为![]() ,
,
![]()
∵![]() 为已知圆的直径,∴
为已知圆的直径,∴![]() ,则
,则![]() .
.
设![]() 、
、![]() ,∵
,∵![]() ,而
,而![]() 、
、![]() 在抛物线上,
在抛物线上,
由已知可知,直线![]() 方程为
方程为![]() ,于是,由方程组
,于是,由方程组
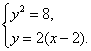 消去
消去![]() ,得
,得![]() ,∴
,∴![]() .
.
∴![]() ,因此,
,因此,![]() .
.
说明:本题如果分别求![]() 与
与![]() 则很麻烦,因此把
则很麻烦,因此把![]() 转化成
转化成![]() 是关键所在,在求
是关键所在,在求![]() 时,又巧妙地运用了抛物线的定义,从而避免了一些繁杂的运算.
时,又巧妙地运用了抛物线的定义,从而避免了一些繁杂的运算.