数列单元试题1

新课标数学必修5第二章数列单元试题

说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答．共100分，考试时间90分钟．

第Ⅰ卷（选择题　共30分）

一、选择题（本大题共10小题，每小题3分，共30分）

1．在正整数100至500之间能被11整除的个数为（　　）

A．34　　　　　　　　　　　　　B．35　　　　　　　　　　　　　C．36　　　　　　　　　　　　　D．37

2．在数列{a_n}中，a₁=1，a_n+1=a_n²－1（n≥1），则a₁+a₂+a₃+a₄+a₅等于（　　）

A．－1　　　　　　　　　　　　B．1　　　　　　　　　　　　　　C．0　　　　　　　　　　　　　　D．2

3．{a_n}是等差数列，且a₁+a₄+a₇=45，a₂+a₅+a₈=39，则a₃+a₆+a₉的值是（　　）

A．24　　　　　　　　　　　　　B．27　　　　　　　　　　　　　C．30　　　　　　　　　　　　　D．33

4．设函数f（x）满足f（n+1）=（n∈N^*）且f（1）=2，则f（20）为（　　）

A．95　　　　　　　　　　　　　B．97　　　　　　　　　　　　　C．105　　　　　　　　　　　　D．192

5．等差数列{a_n}中，已知a₁=－6，a_n=0，公差d∈N^*，则n（n≥3）的最大值为（　　）

A．5　　　　　　　　　　　　　　B．6　　　　　　　　　　　　　　C．7　　　　　　　　　　　　　　D．8

6．设a_n=－n²+10n+11，则数列{a_n}从首项到第几项的和最大（　　）

A．第10项　　　　　　　　 B．第11项　　　　　　　　　C．第10项或11项　　　D．第12项

7．已知等差数列{a_n}的公差为正数，且a₃·a₇=－12，a₄+a₆=－4，则S₂₀为（　　）

A．180　　　　　　　　　　　　B．－180　　　　　　　　　　 C．90　　　　　　　　　　　　　D．－90

8．现有200根相同的钢管，把它们堆放成正三角形垛，要使剩余的钢管尽可能的少，那么剩余钢管的根数为（　　）

A．9　　　　　　　　　　　　　　B．10　　　　　　　　　　　　　C．19　　　　　　　　　　　　　D．29

9．由公差为d的等差数列a₁、a₂、a₃…重新组成的数列a₁+a₄， a₂+a₅， a₃+a₆…是（　　）

A．公差为d的等差数列　　　　　　　　　　　　　　　　 B．公差为2d的等差数列

C．公差为3d的等差数列　　　　　　　　　　　　　　　 D．非等差数列

10．在等差数列{a_n}中，若S₉=18，S_n=240，a_n－4=30，则n的值为（　　）

A．14　　　　　　　　　　　　　B．15　　　　　　　　　　　　　C．16　　　　　　　　　　　　　D．17

第Ⅱ卷（非选择题　共70分）

二、填空题（本大题共4小题，每小题4分，共16分）

11．在数列{a_n}中，a₁=1，a_n+1=（n∈N^*），则是这个数列的第_________项．

12．在等差数列{a_n}中，已知S₁₀₀=10，S₁₀=100，则S₁₁₀=_________．

13．在－9和3之间插入n个数，使这n+2个数组成和为－21的等差数列，则n=_______．

14．等差数列{a_n}，{b_n}的前n项和分别为S_n、T_n，若=，则=_________．

三、解答题（本大题共5小题，共54分．解答应写出文字说明、证明过程或演算步骤）

15．（本小题满分8分）若等差数列5，8，11，…与3，7，11，…均有100项，问它们有多少相同的项？

16．（本小题满分10分）在等差数列{a_n}中，若a₁=25且S₉=S₁₇，求数列前多少项和最大．

17．（本小题满分12分）数列通项公式为a_n=n²－5n+4，问

（1）数列中有多少项是负数？（2）n为何值时，a_n有最小值？并求出最小值．

18．（本小题满分12分）甲、乙两物体分别从相距70 m的两处同时相向运动，甲第一分钟走2 m，以后每分钟比前1分钟多走1 m，乙每分钟走5 m．

（1）甲、乙开始运动后，几分钟相遇．

（2）如果甲、乙到达对方起点后立即折返，甲继续每分钟比前1分钟多走1 m，乙继续每分钟走5 m，那么开始运动几分钟后第二次相遇？

19．（本小题满分12分）已知数列{a_n}的前n项和为S_n，且满足a_n+2S_n·S_n－1=0（n≥2），a₁=．

（1）求证：{}是等差数列；

（2）求a_n表达式；

（3）若b_n=2（1－n）a_n（n≥2），求证：b₂²+b₃²+…+b_n²<1．

参考答案：

1. 考查等差数列的应用．

【解析】观察出100至500之间能被11整除的数为110、121、132、…它们构成一个等差数列，公差为11，数a_n=110+（n－1）·11=11n+99，由a_n≤500，解得n≤36．4，n∈N^*，∴n≤36．

【答案】C

2. 考查数学建模和探索问题的能力．

【解析】1+2+3+…+n<200，即<200．

显然n=20时，剩余钢管最少，此时用去=190根．

【答案】B

3.考查等差数列的运用．

【解析】由等差数列性质，a₄+a₆=a₃+a₇=－4与a₃·a₇=－12联立，即a₃，a₇是方程x²+4x－12=0的两根，又公差d>0，∴a₇>a₃a₇=2，a₃=－6，从而得a₁=－10，d=2，S₂₀=180．

【答案】A

4.考查等差数列的通项．

【解析】a_n=a₁+（n－1）d，即－6+（n－1）d=0n=+1

∵d∈N^*，当d=1时，n取最大值n=7．

【答案】C

5.考查数列通项的理解及递推关系．

【解析】由已知：a_n+1=a_n²－1=（a_n+1）（a_n－1），

∴a₂=0，a₃=－1，a₄=0，a₅=－1．

【答案】A

6.考查等差数列的性质及运用．

【解析】a₁+a₄+a₇，a₂+a₅+a₈，a₃+a₆+a₉成等差数列，故a₃+a₆+a₉=2×39－45=33．

【答案】D

7.考查递推公式的应用．

【解析】f（n+1）－f（n）=

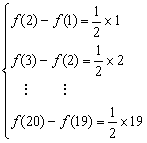
相加得f（20）－f（1）=（1+2+…+19）f（20）=95+f（1）=97．

【答案】B

8.考查数列求和的最值及问题转化的能力．

【解析】由a_n=－n²+10n+11=－（n+1）（n－11），得a₁₁=0，而a₁₀>0，a₁₂<0，S₁₀=S₁₁．

【答案】C

9. 考查等差数列的性质．

【解析】（a₂+a₅）－（a₁+a₄）=（a₂－a₁）+（a₅－a₄）=2d．（a₃+a₆）－（a₂+a₅）=（a₃－a₂）+（a₆－a₅）=2d．依次类推．

【答案】B

10. 考查等差数列的求和及运用．

【解析】S₉==18a₁+a₉=42（a₁+4d）=4．

∴a₁+4d=2，又a_n=a_n－4+4d．∴S_n==16n=240．

∴n=15．

【答案】B

11. 考查数列概念的理解及观察变形能力．

【解析】由已知得=+，∴{}是以=1为首项，公差d=的等差数列．

∴=1+（n－1），∴a_n==，∴n=6．

【答案】6

12. 考查等差数列性质及和的理解．

【解析】S₁₀₀－S₁₀=a₁₁+a₁₂+…+a₁₀₀=45（a₁₁+a₁₀₀）=45（a₁+a₁₁₀）=－90a₁+a₁₁₀=－2．

S₁₁₀=（a₁+a₁₁₀）×110=－110．

【答案】－110

13. 考查等差数列的前n项和公式及等差数列的概念．

【解析】－21=，∴n=5．

【答案】5

14. 考查等差数列求和公式及等差中项的灵活运用．

【解】==．

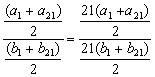【答案】

15. 考查等差数列通项及灵活应用．

【解】设这两个数列分别为{a_n}、{b_n}，则a_n=3n+2，b_n=4n－1，令a_k=b_m，则3k+2=4m－1．

∴3k=3（m－1）+m，∴m被3整除．

设m=3p（p∈N^*），则k=4p－1．

∵k、m∈［1，100］．

则1≤3p≤100且1≤p≤25．

∴它们共有25个相同的项．

16. 考查等差数列的前n项和公式的应用．

【解】∵S₉=S₁₇，a₁=25，∴9×25+d=17×25+d

解得d=－2，∴S_n=25n+（－2）=－（n－13）²+169．

由二次函数性质，故前13项和最大．

注：本题还有多种解法．这里仅再列一种．由d=－2，数列a_n为递减数列．

a_n=25+（n－1）（－2）≥0，即n≤13．5．

∴数列前13项和最大．

17. 【解】（1）由a_n为负数，得n²－5n+4<0，解得1<n<4．

∵n∈N^*，故n=2或3，即数列有2项为负数，分别是第2项和第3项．

（2）∵a_n=n²－5n+4=（n－）²－，∴对称轴为n==2．5

又∵n∈N^*，故当n=2或n=3时，a_n有最小值，最小值为2²－5×2+4=－2．

18. 考查等差数列求和及分析解决问题的能力．

【解】（1）设n分钟后第1次相遇，依题意得2n++5n=70

整理得：n²+13n－140=0，解得：n=7，n=－20（舍去）

∴第1次相遇在开始运动后7分钟．

（2）设n分钟后第2次相遇，依题意有：2n++5n=3×70

整理得：n²+13n－6×70=0，解得：n=15或n=－28（舍去）

第2次相遇在开始运动后15分钟．

19.考查数列求和及分析解决问题的能力．

【解】（1）∵－a_n=2S_nS_n－1，∴－S_n+S_n－1=2S_nS_n－1（n≥2）

S_n≠0，∴－=2，又==2，∴{}是以2为首项，公差为2的等差数列．

（2）由（1）=2+（n－1）2=2n，∴S_n=

当n≥2时，a_n=S_n－S_n－1=－

n=1时，a₁=S₁=，∴a_n=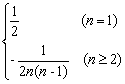

（3）由（2）知b_n=2（1－n）a_n=

∴b₂²+b₃²+…+b_n²=++…+<++…+

=（1－）+（－）+…+（－）=1－<1．