数列单元试题4

新课标数学必修5第2章数列单元试题（4）

说明：本试卷分为第Ⅰ、Ⅱ卷两部分，请将第Ⅰ卷选择题的答案填入题后括号内，第Ⅱ卷可在各题后直接作答．共100分，考试时间90分钟．

第Ⅰ卷（选择题　共30分）

一、选择题（本大题共10小题，每小题3分，共30分）

1．互不相等的三个正数a、b、c成等差数列，又x是a、b的等比中项，y是b、c的等比中项，那么x²、b²、y²这三个数（　　）

A．成等比而非等差　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　B．成等差而非等比

C．既成等比又成等差　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　D．既非等差又非等比

考查数列定义及综合运用．

【解析】依题意：a+c=2b　①　x²=ab　②　y²=bc　③

由②③可得a=，c=代入①式得：+=2bx²+y²=2b²．

【答案】B

2．数列{a_n}中，a₁，a₂－a₁，a₃－a₂，…，a_n－a_n－1…是首项为1、公比为的等比数列，则a_n等于（　　）

A．（1－）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．（1－）

C．（1－）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　D．（1－）

考查等比数列的认识．

【解析】a_n=a₁+（a₂－a₁）+（a₃－a₂）+…+（a_n－a_n－1），

即等比数列的前n项和，依公式可知选A．

【答案】A

3．已知0<a<b<c<1，且a、b、c成等比数列，n为大于1的整数，那么log_an、log_bn、log_cn（　　）

A．成等比数列　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　B．成等差数列

C．倒数成等差数列　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　　　　　D．以上均不对

考查等比、等差数列概念、对数运算．

【解析】由已知ac=b²，又log_na+log_nc=log_nac=log_nb²=2log_nb，故+=．

【答案】C

4．已知1是a²与b²的等比中项，又是与的等差中项，则的值是（　　）

A．1或　　　　　　　　　　　　 B．1或－　　　　　　　　　　　　　　C．1或　　　　　　　　　　　　　　　　D．1或－

考查等比中项以及变形能力．

【解析】依题意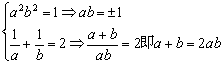

∴原式====，

当ab=1时，原式=1，当ab=－1时，原式=－．

【答案】D

5．S_n=1－2+3－4+5－6+…+（－1）ⁿ⁺¹·n，则S₁₀₀+S₂₀₀+S₃₀₁等于（　　）

A．1　　　　　　　　　　　　　　　　　　　　　　B．－1　　　　　　　　　　　　 　　　　　　C．51　　　　　　　　　　　　　　　　　　　D．52

考查一般数列求和整体代换思想．

【解析】S₁₀₀=－50，S₂₀₀=－100，S₃₀₁=－150+301，故S₁₀₀+S₂₀₀+S₃₀₁=1．

【答案】A

6．正项等比数列{a_n}中，S₂=7，S₆=91，则S₄为（　　）

A．28　　　　　　　　　　　　　　　　　　　　　 B．32　　　　　　　　　　　　　　　　　　　C．35　　　　　　　　　　　　　　　　　　　D．49

考查等比数列性质及应用．

【解析】∵{a_n}为等比数列，∴S₂，S₄－S₂，S₆－S₄也为等比数列，即7，S₄－7，91－S₄成等比数列，即（S₄－7）²=7（91－S₄），解得S₄=28或－21（舍去）．

【答案】A

7．已知数列{a_n}通项a_n=（n∈N^*），则数列{a_n}的前30项中最大的项为（　　）

A．a₃₀B．a₁₀C．a₉ D．a₁

考查数列通项意义及变形能力．

【解析】a_n=1+，∴a₁₀最大．

【答案】B

8．在等比数列{a_n}中，已知n∈N^*，且a₁+a₂+…+a_n=2ⁿ－1，那么a₁²+a₂²+…+a_n²等于（　　）

A．4ⁿ－1　　　　　　　　　　　　　B．（4ⁿ－1）　　　　　　　　　　　 C．（2ⁿ－1）²D．（2ⁿ－1）²

考查等比数列概念、求和．

【解析】由S_n=2ⁿ－1，易求得a_n=2^n－1，a₁=1，q=2，∴{a_n²}是首项为1，公比为4的等比数列，由求和公式易知选B．

【答案】B

9．数列1，1+2，1+2+2²，…，1+2+2²+…+2^n－1，…的前n项和为（　　）

A．2ⁿ－n－1　　　　　　　　　　　　　　　　 B．2ⁿ⁺¹－n－2　　　　　　　C．2ⁿ D．2ⁿ⁺¹－n

考查一般数列求和的技巧．

【解析】a_n=2ⁿ－1，∴S_n=（2+2²+…+2ⁿ）－n=2ⁿ⁺¹－n－2．

【答案】B

10．若{a_n}的前8项的值各异，且a_n+8=a_n，对于n∈N^*都成立，则下列数列中，可取遍{a_n}前8项的值的数列为（　　）

A．{a_2k+1}　　　　　　 　　　　　　B．{a_3k+1}　　　　　　　　　　　　　　　　C．{a_4k+1}　　　　　　　　　　　　　　　 D．{a_6k+1}

考查数列基本知识及分析问题能力．

【解析】∵k∈N^*，k=1、2、3…

当k=1、2、3…7、8时，a_2k+1均取奇数项，而无偶数项，∴{a_2k+1}不符．

而当k取以上值时，{a_3k+1}可以取遍前8项．

【答案】B

第Ⅱ卷（非选择题　共70分）

二、填空题（本大题共4小题，每小题4分，共16分）

11．在等比数列{a_n}中，已知S_n=3ⁿ+b，则b的值为_______．

考查等比数列求和公式的本质形式．

【解析】a₁=S₁=3+b，n≥2时，a_n=S_n－S_n－1=2×3^n－1．

a_n为等比数列，∴a₁适合通项，2×3^1－1=3+b，∴b=－1．

【答案】－1

12．已知等差数列lgx₁，lgx₂，…，lgx_n的第r项为s，第s项为r（0<r<s），则x₁+x₂+…+x_n=_______．

考查数学化归能力．

【解析】

lgx_n+1－lgx_n=－1=．

∴{x_n}为等比数列，且q=．

∴x₁+x₂+…+x_n==．

【答案】

13．若{a_n}是递增数列，对于任意自然数n，a_n=n²+λn恒成立，则实数λ的取值范围是_______．

考查数列和不等式基本知识．

【解析】因为{a_n}为递增数列，∴n²+λn>（n－1）²+λ（n－1）（n≥2）

即2n－1>－λ（n≥2）λ>1－2n（n≥2）

要使n∈N^*恒成立，则λ>－3．

【答案】λ>－3

14．每次用相同体积的清水洗一件衣物，且每次能洗去污垢的，若洗n次后，存在的污垢在1%以下，则n的最小值为_________．

考查把实际问题转化为数学问题的能力．

【解析】每次能洗去污垢的，就是存留了，故洗n次后，还有原来的（）ⁿ，由题意，有：（）ⁿ<1%，∴4ⁿ>100得n的最小值为4．

【答案】4

三、解答题（本大题共5小题，共54分．解答应写出文字说明、证明过程或演算步骤）

15．（本小题满分8分）已知公差不为0的等差数列{a_n}中，a₁+a₂+a₃+a₄=20，a₁，a₂，a₄成等比数列，求集合A={xx=a_n，n∈N^*且100<x<200}的元素个数及所有这些元素的和．

考查等差、等比数列概念、求和公式及集合基本知识的应用．

【解】设{a_n}公差为d，则a₂=a₁+d，a₄=a₁+3d

∵a₁、a₂、a₄成等比数列，∴（a₁+d）²=a₁（a₁+3d）d=a₁．

又∵a₁+（a₁+d）+（a₁+2d）+（a₁+3d）=4a₁+6d=20．

解得：a₁=d=2，∴x=a_n=2+2（n－1）=2n

∴A={xx=2n，n∈N^*且100<x<200}

∵100<2n<200，∴50<n<100．

∴集合A中元素个数100－50－1=49（个）

由求和公式得：S=×49=7350．

16．（本小题满分10分）已知等差数列{a_n}中，a₂=8，前10项和S₁₀=185．

（1）求通项；

（2）若从数列{a_n}中依次取第2项、第4项、第8项…第2ⁿ项……按原来的顺序组成一个新的数列{b_n}，求数列{b_n}的前n项和T_n．

考查等差、等比数列性质、求和公式及转化能力．

【解】（1）设{a_n}公差为d，有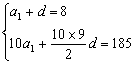

解得a₁=5，d=3

∴a_n=a₁+（n－1）d=3n+2

（2）∵b_n=a=3×2ⁿ+2

∴T_n=b₁+b₂+…+b_n=（3×2¹+2）+（3×2²+2）+…+（3×2ⁿ+2）=3（2¹+2²+…+2ⁿ）+2n=6×2ⁿ+2n－6．

17．（本小题满分12分）设{a_n}为等差数列，{b_n}为等比数列，a₁=b₁=1，a₂+a₄=b₃，b₂·b₄=a₃，分别求出{a_n}及{b_n}的前10项和S₁₀和T₁₀．

考查等差数列、等比数列的性质及求和．

【解】∵{a_n}为等差数列，{b_n}为等比数列．

∴a₂+a₄=2a₃，b₂·b₄=b₃²

由已知a₂+a₄=b₃，b₂b₄=a₃，

∴b₃=2a₃，a₃=b₃²b₃=2b₃²，

∵b₃≠0，∴b₃=，a₃=．

由a₁=1，a₃={a_n}公差d=－．

∴S₁₀=10a₁+d=－

由b₁=1，b₃=，知{b_n}公比为q=±．

当q=时，T₁₀=（2+）

当q=－时，T₁₀=（2－）．

18．（本小题满分12分）已知{a_n}的前n项和为S_n，且a_n+S_n=4．

（1）求证：数列{a_n}是等比数列；

（2）是否存在正整数k，使>2成立．

考查数列通项与前n项和关系及综合分析能力．

【解】（1）由题意，S_n+a_n=4，S_n+1+a_n+1=4，

∴（S_n+1+a_n+1）－（S_n+a_n）=0

即2a_n+1－a_n=0，a_n+1=a_n，

又2a₁=S₁+a₁=4，∴a₁=2．

∴数列{a_n}是以首项a₁=2，公比为q=的等比数列．

（2）S_n=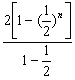=4－2^2－n．

∵k∈N^*，∴2^k－1∈N^*．

这与2^k－1∈（1，）相矛盾，故不存在这样的k，使不等式成立．

19．（本小题满分12分）已知函数f（x）=（）^x+a的反函数f^－1（x）的图象过原点．

（1）若f^－1（x－3），f^－1（－1），f^－1（x－4）成等差数列，求x的值；

（2）若互不相等的三个正数m、n、t成等比数列，问f^－1（m），f^－1（t），f^－1（n）能否组成等差数列，并证明你的结论．

考查函数与反函数概念、等差、等比的判定及综合知识能力．

【解】（1）∵f^－1（x）图象过（0，0），可知原函数过（0，0）

∴有（）⁰+a=0a=－1

∴f（x）=（）^x－1，值域{yy>－1}

由y+1=（）^xx=log（y+1）

∴f^－1（x）=log（x+1）（x>－1）

∵f^－1（x－3）=log（x－2），f^－1（－1）=log=1，

f^－1（x－4）=log（x－3）

∴log（x－2）（x－3）=（）²=2

解得：x₁=4，x₂=1，

而又∵x>3，∴x=4．

（2）假设f^－1（m），f^－1（t），f^－1（n）组成等差数列，则有：

2log（t+1）=log（m+1）+log（n+1）

即（t+1）²=（m+1）（n+1）

化简得：2t=m+n①

又∵m、t、n成等比数列

∴t²=mnt=代入①式

得2=m+n即（－）²=0

∴m=n，这与已知三数m、n、t互不相等矛盾．

∴f^－1（m）、f^－1（t）、f^－1（n）不能组成等差数列．