典型例题一
例1 直线![]() 过点
过点![]() (-1,3),倾斜角的正弦是
(-1,3),倾斜角的正弦是![]() ,求直线
,求直线![]() 的方程.
的方程.
分析:根据倾斜角的正弦求出倾斜角的正切,注意有两解.
解:因为倾斜角![]() 的范围是:
的范围是:![]()
又由题意:![]() ,
,
所以:![]() ,
,
直线过点![]() (-1,3),由直线的点斜式方程得到:
(-1,3),由直线的点斜式方程得到:![]()
即:![]() 或
或![]() .
.
说明:此题是直接考查直线的点斜式方程,在计算中,要注意当不能判断倾斜角![]() 的正切时,要保留斜率的两个值,从而满足条件的解有两个.
的正切时,要保留斜率的两个值,从而满足条件的解有两个.
典型例题二
例2 求经过两点![]() (2,
(2,![]() )和
)和![]() (
(![]() ,3)的直线方程.
,3)的直线方程.
分析:本题有两种解法,一是利用直线的两点式;二是利用直线的点斜式.在解答中如果选用点斜式,只涉及到![]() 与2的分类;如果选用两点式,还要涉及
与2的分类;如果选用两点式,还要涉及![]() 与3的分类.
与3的分类.
解:法一:利用直线的两点式方程
∵直线过两点![]() (2,
(2,![]() )和
)和![]() (
(![]() ,3)
,3)
(1)当![]() 时,点
时,点![]() 的坐标是
的坐标是![]() (2,3),与点
(2,3),与点![]() (
(![]() ,3)的纵坐标相等,则直线
,3)的纵坐标相等,则直线![]() 的方程是
的方程是![]() ;
;
(2)当![]() 时,点
时,点![]() 的坐标是
的坐标是![]() (2,3),与点
(2,3),与点![]() (2,
(2,![]() )的横坐标相等,则直线
)的横坐标相等,则直线![]() 的方程是
的方程是![]() ;
;
(3)当![]() ,
,![]() 时,由直线的两点式方程
时,由直线的两点式方程![]() 得:
得:
![]()
法二:利用直线的点斜式方程
(1)当![]() 时,点
时,点![]() 的横坐标相同,直线
的横坐标相同,直线![]() 垂直与
垂直与![]() 轴,则直线
轴,则直线![]() 的
的![]() ;
;
(2)当![]() 时,过点
时,过点![]() 的直线的斜率是
的直线的斜率是![]() ,
,
又∵过点![]() (2,
(2,![]() )
)
∴由直线的点斜式方程![]() 得过点
得过点![]() 的直线的方程是:
的直线的方程是:
![]()
说明:本题的目的在于使学生理解点斜式和两点式的限制条件,并体会分类讨论的思想方法.
典型例题三
例3 把直线方程![]() 化成斜截式______,化成截距式______.
化成斜截式______,化成截距式______.
分析:因为![]() ,即
,即![]() ,
,![]() ,
,![]() ,按斜截式、截距式的形式要求变形即可.
,按斜截式、截距式的形式要求变形即可.
解:斜截式为![]() ,截距式为
,截距式为![]() +
+![]() =1
=1
说明:此题考查的是直线方程的两种特殊形式:斜截式和截距式.
典型例题四
例4 直线![]() 的倾斜角的取值范围是_____________.
的倾斜角的取值范围是_____________.
分析:将直线的方程化为斜截式,得出直线的斜率,再由斜率和倾斜角的关系,得出关于![]() 的一个三角不等式即可.
的一个三角不等式即可.
解:已知直线的方程为![]() ,其斜率
,其斜率![]() .
.
由![]() ,得
,得![]() ,
,
即![]() .
.
由![]() ,得
,得![]() .
.
说明:解题易得出错误的结果![]() ,其原因是没有注意到倾斜角的取值范围.
,其原因是没有注意到倾斜角的取值范围.
典型例题五
例5 直线![]() 经过点
经过点![]() ,且在两坐标轴上的截距相等,求直线
,且在两坐标轴上的截距相等,求直线![]() 的方程.
的方程.
分析:借助点斜式求解,或利用截距式求解.
解法一:由于直线![]() 在两轴上有截距,因此直线不与
在两轴上有截距,因此直线不与![]() 、
、![]() 轴垂直,斜率存在,且
轴垂直,斜率存在,且![]() .
.
设直线方程为![]() ,
,
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() .
.
由题设可得![]() ,解得
,解得![]() 或
或![]() .
.
所以,![]() 的方程为
的方程为![]() 或
或![]() .
.
故直线![]() 的方程为
的方程为![]() 或
或![]() .
.
解法二:由题设,设直线![]() 在
在![]() 、
、![]() 轴的截距均为
轴的截距均为![]() .
.
若![]() ,则
,则![]() 过点
过点![]() ,又过点
,又过点![]() ,
,
∴![]() 的方程为
的方程为![]() ,即
,即![]() :
:![]() .
.
若![]() ,则设
,则设![]() 为
为![]() .
.
由![]() 过点
过点![]() ,知
,知![]() ,故
,故![]() .
.
∴![]() 的方程
的方程![]() .
.
综上可知,直线![]() 的方程为
的方程为![]() 或
或![]() .
.
说明:对本例,常见有以下两种误解:
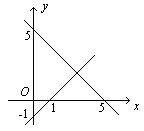
误解一:如下图,由于直线![]() 的截距相等,故直线
的截距相等,故直线![]() 的斜率的值为
的斜率的值为![]() .若
.若![]() ,则直线方程为
,则直线方程为![]() ;若
;若![]() ,则直线方程为
,则直线方程为![]() .故直线方程为
.故直线方程为![]() 或
或![]() .
.
误解二:由题意,直线在两轴上的截距相等,则可设直线方程为![]() .由直线过点
.由直线过点![]() ,得
,得![]() ,即
,即![]() ,也即方程为
,也即方程为![]() .
.
在上述两种误解中,误解一忽视了截距的意义,截距不是距离,它可正可负,也可以为0.显见,当![]() 时,直线
时,直线![]() 的两轴上的截距分别为1和-1,它们不相等.另外,这种解法还漏掉了直线在两轴上的截距均为0的这种特殊情形.误解二中,没有注意到截距式方程的适用范围,同样也产生了漏解.
的两轴上的截距分别为1和-1,它们不相等.另外,这种解法还漏掉了直线在两轴上的截距均为0的这种特殊情形.误解二中,没有注意到截距式方程的适用范围,同样也产生了漏解.
典型例题六
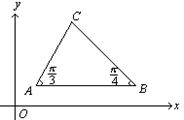
例6 已知在第一象限的![]() 中,
中,![]() 、
、![]() ,
,![]() ,
,![]() ,求:
,求:
(1)![]() 边的方程;(2)
边的方程;(2)![]() 和
和![]() 所在直线的方程.
所在直线的方程.
分析:(1)当直线与![]() 轴平行时或垂直时,不能用两点式求直线的方程.(2)由图可知
轴平行时或垂直时,不能用两点式求直线的方程.(2)由图可知![]() 、
、![]() 的斜率,根据点斜式方程即可得出结果.
的斜率,根据点斜式方程即可得出结果.
解:(1)如图,![]() 的方程为
的方程为![]()
![]() .
.
(2)由![]() ∥
∥![]() 轴,且
轴,且![]() 在第一象限知
在第一象限知
![]() 的斜率
的斜率![]() ,
,![]() 的斜率
的斜率![]() .
.
所以,![]() 边所在直线的方程为
边所在直线的方程为![]() ,即
,即![]() .
.
![]() 边所在直线的方程为
边所在直线的方程为![]() ,即
,即![]() .
.
说明:(1)![]() 边是一条线段,要注意变量
边是一条线段,要注意变量![]() 的取值范围.(2)解题中,要注意画出图形,便于直观地得到所求直线所具备的条件.
的取值范围.(2)解题中,要注意画出图形,便于直观地得到所求直线所具备的条件.
典型例题七
例7 若![]() 的顶点
的顶点![]() ,
,![]() ,
,![]() ,求
,求![]() 的平分线
的平分线![]() 所在的直线的方程.
所在的直线的方程.
分析:两个条件确定一条直线.要求![]() 的方程,已知点
的方程,已知点![]() 的坐标,只要再找出
的坐标,只要再找出![]() 的斜率或点
的斜率或点![]() 的坐标就可以了.在三角形中,
的坐标就可以了.在三角形中,![]() 的平分线有下列性质:(1)
的平分线有下列性质:(1)![]() ;(2)
;(2)![]() 上任一点到两边
上任一点到两边![]() 、
、![]() 的距离相等;(3)
的距离相等;(3)![]() .用其中任何一个性质,都可以确定第二个条件.
.用其中任何一个性质,都可以确定第二个条件.
解法一:∵![]() ,
,
![]() ,
,
∴![]() 分
分![]() 所成的比为
所成的比为![]() .
.
设![]() 的坐标为
的坐标为![]() ,则:
,则:
![]() ,
,![]() ,
,
即![]() .
.
由两点式得![]() 的方程为
的方程为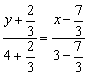 ,即
,即![]() .
.
解法二:直线![]() 到
到![]() 的角等于
的角等于![]() 到
到![]() 的角,
的角,
![]() ,
,![]() .
.
设![]() 的斜率为
的斜率为![]() (
(![]() 或
或![]() ),则有
),则有
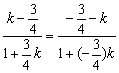 .
.
解得![]() 或
或![]() (舍去).
(舍去).
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
解法三:设直线![]() 上动点
上动点![]() ,则
,则![]() 点到
点到![]() 、
、![]() 的距离相等,即:
的距离相等,即:
![]() ,
,
∴![]() 或
或![]()
结合图形分析,知![]() 是
是![]() 的角
的角![]() 的外角平分线,舍去.
的外角平分线,舍去.
所以所求的方程为![]() .
.
说明:(1)确定不同条件下的直线方程是高考的重要内容,其方法主要是待定系数法(如解法一、解法二)和轨迹法(如解法三).要熟练掌握直线方程各种形式间的相互转化.点斜式是直线方程最重要的一种形式,要加强这方面的训练.
(2)解法三涉及到后面将要学到的知识.这里先把它列出来,作为方法积累.
典型例题八
例8 求过点![]() 且分别满足下列条件的直线方程:
且分别满足下列条件的直线方程:
(1)与两坐标轴围成的三角形面积为5;
(2)与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,且
两点,且![]() .
.
分析:对于(1),既可借助于截距式求解,也可以利用点斜式来求解;对于(2),利用截距式求解较为简便.
解法一:设所求的直线方程为![]() .
.
由直线过点![]() ,得
,得![]() ,即
,即![]() .
.
又![]() ,故
,故![]() .
.
联立方程组![]() 解得
解得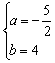 或
或![]() .
.
故所求直线方程为 和
和![]() ,即:
,即:
![]() 和
和![]() .
.
解法二:设所求直线方程为![]() ,它与两坐轴的交点为
,它与两坐轴的交点为![]() ,
,![]() .
.
由已知,得![]() ,即
,即![]() .
.
当![]() 时,上述方程可变成
时,上述方程可变成![]() ,
,
解得![]() ,或
,或![]() .
.
由此便得欲求方程为![]() 和
和![]() .
.
(2)解:由![]() 是
是![]() 的分点,得
的分点,得![]() .
.
设点![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.
当![]() 是
是![]() 的内分点时,
的内分点时,![]() .
.
由定比分点公式得![]() ,
,![]() .
.
再由截距式可得所求直线方程为![]() .
.
当点![]() 是
是![]() 的外分点时,
的外分点时,![]() .
.
由定比分点公式求得![]() ,
,![]() .
.
仿上可得欲求直线方程为![]() .
.
故所求的直线方程为![]() ,或
,或![]() .
.
说明:对于(1),应注意对题意的理解,否则,就较易得到![]() ,且
,且![]() ,从而遗漏了
,从而遗漏了![]() 的情形;对于(2),应当区分内分点与外分点两种不同的情形.必要时,可画出草图直观地加以分析,防止漏解.
的情形;对于(2),应当区分内分点与外分点两种不同的情形.必要时,可画出草图直观地加以分析,防止漏解.
求直线的方程时,除应注意恰当地选择方程的形式外,还应注意到不同形式的方程的限制条件.如点斜式的限定条件是直线必须存在斜率;截距式的限定条件为两轴上的截距都存在且不为0;两点式的限定条件是直线不与![]() 轴垂直,也不与
轴垂直,也不与![]() 轴垂直.除此以外,还应注意直线方程形式之间的相互转化.
轴垂直.除此以外,还应注意直线方程形式之间的相互转化.
典型例题九
例9 已知两直线![]() 和
和![]() 的交点为
的交点为![]() ,求过两点
,求过两点![]() 、
、![]() 的直线方程.
的直线方程.
分析:利用点斜式或直线与方程的概念进行解答.
解法一:∵![]() 在已知直线上,
在已知直线上,
∴![]()
∴![]() ,即
,即![]() .
.
故所求直线方程为![]() .
.
∴![]() ,即
,即![]() .
.
解法二:∵点![]() 在已知直线上,
在已知直线上,
∴![]()
可见![]() 、
、![]() 都满足方程
都满足方程![]() ,
,
∴过![]() 、
、![]() 两点的直线方程为
两点的直线方程为![]() .
.
说明:解法二充分体现了“点在直线上,则点的坐标满足直线方程;反之,若点的坐标满足方程,则直线一定过这个点”.此解法独特,简化了计算量,能培养学生的思维能力.
典型例题十
例10 过点![]() 引一条直线,使它在两条坐标轴上的截距为正值,且它们的和最小,求这条直线方程.
引一条直线,使它在两条坐标轴上的截距为正值,且它们的和最小,求这条直线方程.
分析:利用直线方程的点斜式,通过两截距之和最小求出直线的斜率,从而求出直线方程.或借助直线方程的截距式,通过两截距之和最小,求出直线在两轴上的截距,从而求出直线的方程.
解法一:设所求的直线方程为![]() .
.
显见,上述直线在![]() 轴、
轴、![]() 轴上的截距分别为
轴上的截距分别为![]() 、
、![]() .
.
由于![]() ,且
,且![]() 可得
可得![]() .
.
直线在两坐标轴上的截距之和为:
![]() ,当且仅当
,当且仅当![]() ,即
,即![]() 时,
时,![]() 最小值为9.
最小值为9.
故所求直线方程为![]() ,即
,即![]() .
.
解法二:设欲求的直线方程为![]() (
(![]() ,
,![]() ).
).
据题设有![]() , ①
, ①
令![]() . ②
. ②
①×②,有![]() .
.
当且仅当![]() 时,即
时,即![]() ,且
,且![]() ,也即
,也即![]() ,
,![]() 时,取等号.
时,取等号.
故所求的直线方程为![]() ,即
,即![]() .
.
说明:在解法一中,应注意到![]() 这个隐含条件.否则,由
这个隐含条件.否则,由![]() ,将很有可能得出错误的结果.如
,将很有可能得出错误的结果.如![]() ,
,![]() 等等.
等等.
在解法二中,应注意运算过程中的合理性,即讲究算理,不然,将会使运算过程不胜其繁.如采取下述方法:由①,用![]() 来表示
来表示![]() ,再代入②中,把
,再代入②中,把![]() 化归成
化归成![]() 的函数.从解题思维方法上说无可厚非,但这种方法将使运算难度陡然增加.不如保持本质、顺其自然好.
的函数.从解题思维方法上说无可厚非,但这种方法将使运算难度陡然增加.不如保持本质、顺其自然好.
典型例题十一
例11 已知![]() ,其中
,其中![]() 、
、![]() 是实常数,求证:直线
是实常数,求证:直线![]() 必过一定点.
必过一定点.
分析与解:观察条件与直线方程的相似之处,可把条件变形为![]() ,可知
,可知![]() ,
,![]() 即为方程
即为方程![]() 的一组解,所以直线
的一组解,所以直线![]() 过定点(6,4).
过定点(6,4).
说明:此问题属于直线系过定点问题,此类问题的彻底解决宜待学完两直线位置之后较好,当然现在也可以研究,并且也有一般方法.
典型例题十二
例12 直线![]() 过点
过点![]() (2,1),且分别交
(2,1),且分别交![]() 轴、
轴、![]() 轴的正半轴于点
轴的正半轴于点![]() 、
、![]() .点
.点![]() 是坐标原点,(1)求当
是坐标原点,(1)求当![]() 面积最小时直线
面积最小时直线![]() 的方程;(2)当
的方程;(2)当![]()
![]() 最小时,求直线
最小时,求直线![]() 的方程.
的方程.
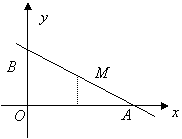 解:(1)如图,设
解:(1)如图,设![]()
![]() ,
,![]()
![]() ,
,![]() 的面积为
的面积为![]() ,则
,则
![]()
并且直线![]() 的截距式方程是
的截距式方程是
![]() +
+![]() =1
=1
由直线通过点(2,1),得
![]() +
+![]() =1
=1
所以:![]() =
=![]() =
=![]()
因为![]() 点和
点和![]() 点在
点在![]() 轴、
轴、![]() 轴的正半轴上,所以上式右端的分母
轴的正半轴上,所以上式右端的分母![]() .由此得:
.由此得:![]()
![]()
![]()
![]()
当且仅当![]()
![]() ,即
,即![]() 时,面积
时,面积![]() 取最小值4,
取最小值4,
这时![]() ,直线的方程是:
,直线的方程是:![]() +
+![]() =1
=1
即:![]()
(2)设![]() ,则
,则![]() =
=![]() ,
,![]() =
=![]() ,如图,
,如图,
所以 ![]()
![]() =
=![]()
![]() =
=![]()
当![]() =45°时
=45°时![]()
![]() 有最小值4,此时
有最小值4,此时![]() ,直线
,直线![]() 的方程为
的方程为![]() .
.
说明:此题与不等式、三角联系紧密,解法很多,有利于培养学生发散思维,综合能力和灵活处理问题能力.动画素材中有关于此题的几何画板演示.
典型例题十三
例13 一根铁棒在20°时,长10.4025米,在40°时,长10.4050米,已知长度l和温度t的关系可以用直线方程来表示,试求出这个方程,并且根据这个方程,求这跟铁棒在25°时的长度.
解:这条直线经过两点(20,10.4025)和(20,10.4050),根据直线的两点式方程,得:
![]() =
=![]()
即
![]() =0.0025
=0.0025![]() +10.4000
+10.4000
当![]() =25°时
=25°时 ![]() =0.0025
=0.0025![]() +10.4000=0.0031+10.4000=10.4031
+10.4000=0.0031+10.4000=10.4031
即当![]() =25°时,铁棒长为10.4031米.
=25°时,铁棒长为10.4031米.
说明:直线方程在实际中应用非常广泛.
典型例题十三
例13 一根铁棒在20°时,长10.4025米,在40°时,长10.4050米,已知长度l和温度t的关系可以用直线方程来表示,试求出这个方程,并且根据这个方程,求这跟铁棒在25°时的长度.
解:这条直线经过两点(20,10.4025)和(20,10.4050),根据直线的两点式方程,得:
![]() =
=![]()
即
![]() =0.0025
=0.0025![]() +10.4000
+10.4000
当![]() =25°时
=25°时 ![]() =0.0025
=0.0025![]() +10.4000=0.0031+10.4000=10.4031
+10.4000=0.0031+10.4000=10.4031
即当![]() =25°时,铁棒长为10.4031米.
=25°时,铁棒长为10.4031米.
说明:直线方程在实际中应用非常广泛.