空间的直线与平面单元测试卷

《空间的直线与平面》单元测试卷

（时间：100分钟　 满分：100分）

班级___________学号___________姓名_______________得分__________________

　　　　　　　　　　　　　　　　　　　　　　　　　　 命题教师：洪汪宝

一、选择题（本大题共12小题，每小题3分，共36分）

1、下列命题中，正确的是（　　　）。

A.若两个平面有一个公共点，则它们一定相交

B.若两个平面有三个公共点，则它们一定重合

C.垂直于同一直线的两直线互相平行

D.两条平行直线中的一条平行于一个已知平面，则另一条也平行于该平面

2、以空间不重合三个平面能把空间分成的部分数为元素的集合是（　　　 ）。

A.{3，4，5，6}　 B.{2，4，6，7}　　　C.{4，6，7，8}　　D.以上都不是

3、已知平面α∩平面β=直线a，A,B∈α,C∈β,Ca,直线AB∩a=D，过A、B、C三点确定平面γ，则平面β与γ的交线必通过（　　　）。

A.点A　　　　　 　　　　　　　　 B.点B　　　

C.点C但不通过点D　　　　　　　  D.点C和点D

4、在长方体ABCD-A₁B₁C₁D₁中，O为B₁D₁的中点，直线A₁C交平面AB₁D₁于点M，则下列结论错误的是（　　  ）

A.A，M，O三点共线　　　　　　  B.A，M，O，A₁四点共面

C.A，O，C，M四点共面　　　　　 D.B，B₁，O，M四点共面

5、两条异面直线在同一平面内的射影一定是（　　　 ）。

　A.两条平行直线　　　　　　　　　　　B.两条相交直线

C.两条相交或平行直线　　　　　　　  D.以上都不对

6、直线垂直于梯形的两底边所在直线是它垂直于梯形所在平面的（　　 ）。

　A.充分不必要条件　　　　　 B.必要不充分条件

　C.充要条件　　　　　　　　 D.既不充分又不必要条件

7、已知△ABC的平面直观图△A₁B₁C₁是边长为a的正三角形，那么原△ABC的面积为（　　　）。

　A.　　  B.　　  C.　　  D.

8、若点E、F、G、H顺次为空间四边形ABCD的四条边AB、BC、CD、DA的中点，且EG=3，FH=4，则AC²+BD²=（　　　 ）。

　A.25　　　　 B.50　　　　C.100　　　  D.200

9、正方体ABCD-A₁B₁C₁D₁中，E、F、G分别为AB、BC、CC₁的中点，则EF与BG所成角的余弦值为（　　　 ）。

　　A.　　　　B.-　　　 C.　　　　 D.-

10、已知矩形ABCD中，AB=3，BC=a，若PA⊥平面AC，在BC边上取一点E，使PE⊥DE，则满足条件的E点有两个时，a的取值范围是（　　　）。

　　A.a＞6　　　　　　　　　　　  B.a≥6　　　　

C.0＜a＜6　　　　　　　　　　 D.0＜a≤6

11、过平面外一点A引斜线段AB、AC，垂线段AO，B、C为斜足，O为垂足，若∠ABO=30°，AO=6，AC⊥BC，则线段BC的长的取值范围是（　　　 ）。

　 A.（0，6）　　　　　　　　　 B.（6，+∞）　　

　C.（0，）　　　　　　　　 D.（，+∞）

12、若直角△ABC的斜边AB在平面内，直角顶点C在平面外，C在平面内的射影为C₁，C₁不在AB上，则△ABC₁是（　　　 ）。

A.直角三角形　　 B.锐角三角形　　

　C.钝角三角形　　 D.锐角三角形或钝角三角形

二、填空题（本大题共4小题，每小题3分，共12分）

13、点D在由△ABC所确定的平面外，E点是AD上不与A、D重合的一点，F在BC的延长线上（不与C重合），则AB、BC、AC、EF、AD、BD中共有____________对异面直线。

14、给你四个命题：

①　　 过直线外一点，有且只有一条直线与该直线平行；

②　　 过直线外一点，有且只有一个平面与该直线平行；

③　　 过平面外一点，有且只有一条直线与该平面平行；

④　　 过平面外一点，有无数条直线与该平面平行。

其中真命题有__________________（写出序号即可）

15、在直角△ABC中，∠ABC=90°，线段CD⊥平面ABC，分别连结AD和BD，若△ABC、△ADC、△DBC的面积分别为S₁、S₂、S₃，则△ABD的面积等于______________________。

16、若P为直角△ABC所在平面外的一点，∠ACB=90°，PC=24，作PO⊥平面ABC于O点，且PO=12，P到AC、BC的距离相等，则P到AC的距离为_____________。

三、解答题（本大题共5小题，第17、18、19、20题各10分，第21题12分，共52分）

17、求证：过两条异面直线中的一条只能作一个平面平行于另一直线。（要求：根据所给图形和题意写出已知、求证及证明过程）

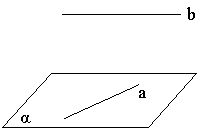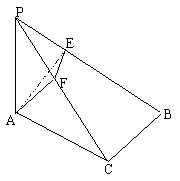18、已知直角△ABC中，∠C=90°，PA⊥平面ABC，且AE⊥PB，AF⊥PC，E，F为垂足。

求证：（1）AF⊥平面PBC；

（2）PB⊥平面AEF。

19、已知平面四边形ABCD在平面α内的射影为一个平行四边形A₁B₁C₁D₁。

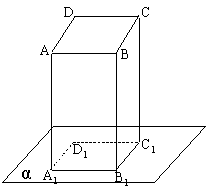求证：（1）平面DD₁C₁C∥平面AA₁B₁B；

（2）四边形ABCD是平行四边形。

20、在正方体ABCD-A₁B₁C₁D₁中，P为DD₁的中点，O为底面ABCD的中心，

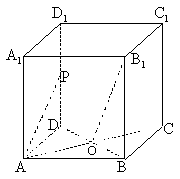求证：B₁O⊥PA。

21、已知棱长为a的正方体ABCD-A₁B₁C₁D₁中，E、F分别是BC、A₁D₁的中点。

（1）　　　 求证：B₁EDF是菱形；

（2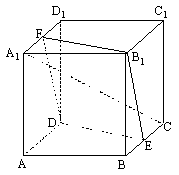）　　　 求A₁C与DE所成的角（用反余弦表示）