典型例题一
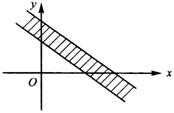
例1 画出不等式组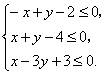 表示的平面区域.
表示的平面区域.
分析:采用“图解法”确定不等式组每一不等式所表示的平面区域,然后求其公共部分.
解:把![]() ,
,![]() 代入
代入![]() 中得
中得![]()
∴ 不等式![]() 表示直线
表示直线![]() 下方的区域(包括边界),
下方的区域(包括边界),
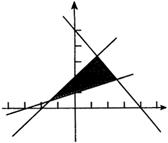
即位于原点的一侧,同理可画出其他两部分,不等式组所表示的区域如图所示.
说明:“图解法”是判别二元一次不等式所表示的区域行之有效的一种方法.
典型例题二
例2 画出![]() 表示的区域,并求所有的正整数解
表示的区域,并求所有的正整数解![]() .
.
分析:原不等式等价于![]() 而求正整数解则意味着
而求正整数解则意味着![]() ,
,![]() 还有限制条件,即求
还有限制条件,即求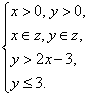 .
.
解:依照二元一次不等式表示的平面区域,知![]() 表示的区域如下图:
表示的区域如下图:
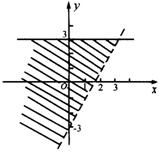
对于![]() 的正整数解,先画出不等式组.
的正整数解,先画出不等式组.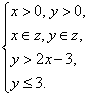 所表示的平面区域,如图所示.
所表示的平面区域,如图所示.
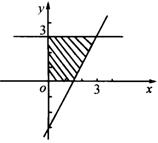
容易求得,在其区域内的整数解为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
说明:这类题可以将平面直角坐标系用网络线画出来,然后在不等式组所表示的平面区域内找出符合题设要求的整数点来.
典型例题三
例3 求不等式组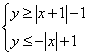 所表示的平面区域的面积.
所表示的平面区域的面积.
分析:本题的关键是能够将不等式组所表示的平面区域作出来,判断其形状进而求出其面积.而要将平面区域作出来的关键又是能够对不等式组中的两个不等式进行化简和变形,如何变形?需对绝对值加以讨论.
解:不等式![]() 可化为
可化为![]() 或
或![]() ;
;
不等式![]() 可化为
可化为![]() 或
或![]() .
.
在平面直角坐标系内作出四条射线
![]() ,
, ![]()
![]() ,
,![]()
则不等式组所表示的平面区域如图
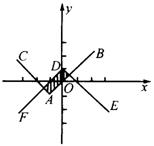
由于![]() 与
与![]() 、
、![]() 与
与![]() 互相垂直,
互相垂直,
所以平面区域是一个矩形.
根据两条平行线之间的距离公式可得矩形的两条边的长度分别为![]() 和
和![]() .
.
所以其面积为![]() .
.
典型例题四
例1 若![]() 、
、![]() 满足条件
满足条件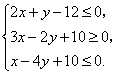 求
求![]() 的最大值和最小值.
的最大值和最小值.
分析:画出可行域,平移直线找最优解.
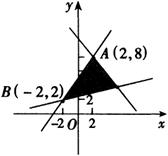
解:作出约束条件所表示的平面区域,即可行域,如图所示.
作直线![]() ,即
,即![]() ,它表示斜率为
,它表示斜率为![]() ,纵截距为
,纵截距为![]() 的平行直线系,当它在可行域内滑动时,由图可知,直线
的平行直线系,当它在可行域内滑动时,由图可知,直线![]() 过点时,
过点时,![]() 取得最大值,当
取得最大值,当![]() 过点
过点![]() 时,
时,![]() 取得最小值.
取得最小值.
∴ ![]() ∴
∴ ![]()
说明:解决线性规划问题,首先应明确可行域,再将线性目标函数作平移取得最值.
典型例题五
例5 用不等式表示以![]() ,
,![]() ,
,![]() 为顶点的三角形内部的平面区域.
为顶点的三角形内部的平面区域.
分析:首先要将三点中的任意两点所确定的直线方程写出来,然后结合图形考虑三角形内部区域应怎样表示。
解:直线![]() 的斜率为:
的斜率为:![]() ,其方程为
,其方程为![]() .
.
可求得直线![]() 的方程为
的方程为![]() .直线
.直线![]() 的方程为
的方程为![]() .
.
![]() 的内部在不等式
的内部在不等式![]() 所表示平面区域内,同时在不等式
所表示平面区域内,同时在不等式![]() 所表示的平面区域内,同时又在不等式
所表示的平面区域内,同时又在不等式![]() 所表示的平面区域内(如图).
所表示的平面区域内(如图).
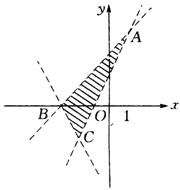
所以已知三角形内部的平面区域可由不等式组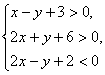 表示.
表示.
说明:用不等式组可以用来平面内的一定区域,注意三角形区域内部不包括边界线.
典型例题六
例6 已知![]() ,
,![]() .求
.求![]() 的最大、最小值.
的最大、最小值.
分析:令![]() ,目标函数是非线性的.而
,目标函数是非线性的.而![]() 可看做区域内的点到原点距离的平方.问题转化为点到直线的距离问题.
可看做区域内的点到原点距离的平方.问题转化为点到直线的距离问题.
解:由![]() 得可行域(如图所示)为
得可行域(如图所示)为![]() ,而
,而![]() 到
到![]() ,
,![]() 的距离分别为
的距离分别为![]() 和
和![]() .
.
所以![]() 的最大、最小值分别是50和
的最大、最小值分别是50和![]() .
.
说明:题目中的目标函数是非线性的.解决的方法类似于线性规划问题.可做出图,利用图进行直观的分析.
典型例题七
例7 设![]() 式中的变量
式中的变量![]() 、
、![]() 满足下列条件
满足下列条件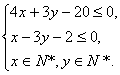 求
求![]() 的最大值.
的最大值.
分析:先作出不等式组所表示的可行域,需要注意的是这里的![]() ,故只是可行域内的整数点,然后作出与直线
,故只是可行域内的整数点,然后作出与直线![]() 平等的直线再进行观察.
平等的直线再进行观察.
解:作出直线![]() 和直线
和直线![]() ,得可行域如图所示.
,得可行域如图所示.
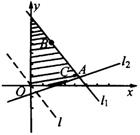
解方程组![]() 得交点
得交点![]() .
.
又作直线![]() ,平等移动过点
,平等移动过点![]() 时,
时,![]() 取最大值,然而点
取最大值,然而点![]() 不是整数点,故对应的
不是整数点,故对应的![]() 值不是最优解,此时过点
值不是最优解,此时过点![]() 的直线为
的直线为![]() ,应考虑可行域中距离直线
,应考虑可行域中距离直线![]() 最近的整点,即
最近的整点,即![]() ,有
,有![]() ,应注意不是找距点
,应注意不是找距点![]() 最近的整点,如点
最近的整点,如点![]() 为可行域中距
为可行域中距![]() 最近的整点,但
最近的整点,但![]() ,它小于
,它小于![]() ,故
,故![]() 的最大值为34.
的最大值为34.
说明:解决这类题的关键是在可行域内找准整点.若将线性目标函数改为非线性目标函数呢?
典型例题八
例8 设![]() ,式中的变量
,式中的变量![]() 、
、![]() 满足
满足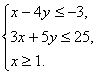 试求
试求![]() 的最大值、最小值.
的最大值、最小值.
分析:作出不等式组所表示的平面区域,本题的关键是目标函数![]() 应理解为可行域中的点与坐标原点的距离的平方.
应理解为可行域中的点与坐标原点的距离的平方.
解:作出直线![]() ,
,![]() ,
,![]() 得到如图所示的可行域.
得到如图所示的可行域.
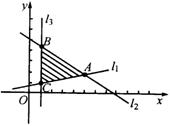
由![]() 得
得![]()
由![]() 得
得![]()
由![]() 得
得![]() .
.
由图可知:当![]() 为点
为点![]() 时,
时,![]() 取最小值为2;当
取最小值为2;当![]() 为点
为点![]() 时,
时,![]() 取最大值29.
取最大值29.
说明:若将该题中的目标函数改为![]() ,如何来求
,如何来求![]() 的最大值、最小值呢?请自己探求.(将目标函数理解为点
的最大值、最小值呢?请自己探求.(将目标函数理解为点![]() 与点
与点![]() 边线的斜率)
边线的斜率)
典型例题九
例9 设![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,用图表示出点
,用图表示出点![]() 的范围.
的范围.
分析:题目中的![]() ,
,![]() 与
与![]() ,
,![]() ,
,![]() 是线性关系.可借助于
是线性关系.可借助于![]() ,
,![]() ,
,![]() 的范围确定
的范围确定![]() 的范围.
的范围.
解:由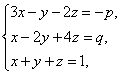 得
得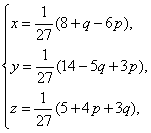 由
由![]() ,
,![]() ,
,![]() 得
得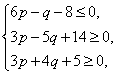 做出不等式所示平面区域如图所示.
做出不等式所示平面区域如图所示.
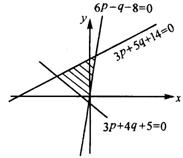
说明:题目的条件隐蔽,应考虑到已有的![]() ,
,![]() ,
,![]() 的取值范围.借助于三元一次方程组分别求出
的取值范围.借助于三元一次方程组分别求出![]() ,
,![]() ,
,![]() ,从而求出
,从而求出![]() ,
,![]() 所满足的不等式组找出
所满足的不等式组找出![]() 的范围.
的范围.
典型例题十
例10 某糖果厂生产![]() 、
、![]() 两种糖果,
两种糖果,![]() 种糖果每箱获利润40元,
种糖果每箱获利润40元,![]() 种糖果每箱获利润50元,其生产过程分为混合、烹调、包装三道工序,下表为每箱糖果生产过程中所需平均时间(单位:分钟)
种糖果每箱获利润50元,其生产过程分为混合、烹调、包装三道工序,下表为每箱糖果生产过程中所需平均时间(单位:分钟)
| 混合 | 烹调 | 包装 | |
|
| 1 | 5 | 3 |
|
| 2 | 4 | 1 |
每种糖果的生产过程中,混合的设备至多能用12机器小时,烹调的设备至多只能用机器30机器小时,包装的设备只能用机器15机器小时,试用每种糖果各生产多少箱可获得最大利润.
分析:找约束条件,建立目标函数.
解:设生产![]() 种糖果
种糖果![]() 箱,
箱,![]() 种糖果
种糖果![]() 箱,可获得利润
箱,可获得利润![]() 元,则此问题的数学模式在约束条件
元,则此问题的数学模式在约束条件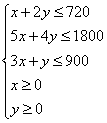 下,求目标函数
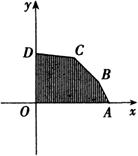
下,求目标函数![]() 的最大值,作出可行域,其边界
的最大值,作出可行域,其边界
![]()
![]()
![]()
![]()
![]()
由![]() 得
得![]() ,它表示斜率为
,它表示斜率为![]() ,截距为
,截距为![]() 的平行直线系,
的平行直线系,![]() 越大,
越大,![]() 越大,从而可知过
越大,从而可知过![]() 点时截距最大,
点时截距最大,![]() 取得了最大值.
取得了最大值.
解方程组![]()
∴ ![]() 即生产
即生产![]() 种糖果120箱,生产
种糖果120箱,生产![]() 种糖果300箱,可得最大利润19800元.
种糖果300箱,可得最大利润19800元.
说明:由于生产![]() 种糖果120箱,生产
种糖果120箱,生产![]() 种糖果300箱,就使得两种糖果共计使用的混合时间为120+2×300=720(分),烹调时间5×120+4×300=1800(分),包装时间3×120+300=660(分),这说明该计划已完全利用了混合设备与烹调设备的可用时间,但对包装设备却有240分钟的包装时间未加利用,这种“过剩”问题构成了该问题的“松驰”部分,有待于改进研究.
种糖果300箱,就使得两种糖果共计使用的混合时间为120+2×300=720(分),烹调时间5×120+4×300=1800(分),包装时间3×120+300=660(分),这说明该计划已完全利用了混合设备与烹调设备的可用时间,但对包装设备却有240分钟的包装时间未加利用,这种“过剩”问题构成了该问题的“松驰”部分,有待于改进研究.
典型例题十一
例11 甲、乙、丙三种食物的维生素![]() 、
、![]() 含量及成本如下表:
含量及成本如下表:
| 甲 | 乙 | 丙 | |
| 维生素 | 600 | 700 | 400 |
| 维生素 | 800 | 400 | 500 |
| 成本(元/千克) | 11 | 9 | 4 |
某食物营养研究所想用![]() 千克甲种食物,
千克甲种食物,![]() 千克乙种食物,
千克乙种食物,![]() 千克丙种食物配成100千克的混合食物,并使混合食物至少含56000单位维生素
千克丙种食物配成100千克的混合食物,并使混合食物至少含56000单位维生素![]() 和63000单位维生素
和63000单位维生素![]() .(1)用
.(1)用![]() 、
、![]() 表示混合物成本
表示混合物成本![]() .(2)确定
.(2)确定![]() 、
、![]() 、
、![]() 的值,使成本最低.
的值,使成本最低.
分析:找到线性约束条件及目标函数,用平行线移动法求最优解.
解:(1)依题意:![]() 、
、![]() 、
、![]() 满足
满足![]()
∴ 成本![]() (元)
(元)
(2)依题意![]()
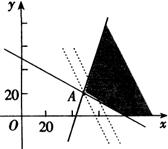 ∵
∵ ![]() ∴
∴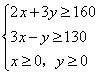
作出不等式组所对应的可行域,如图所示.
联立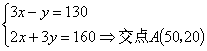
作直线![]() 则易知该直线截距越小,
则易知该直线截距越小,![]() 越小,所以该直线过
越小,所以该直线过![]() 时,直线在
时,直线在![]() 轴截距最小,从而
轴截距最小,从而![]() 最小,此时7×50+5×20+400=
最小,此时7×50+5×20+400=![]() =850元
=850元
∴ ![]() 千克,
千克,![]() 千克时成本最低.
千克时成本最低.
典型例题十二
例12 某工厂有甲、乙两种产品,按计划每天各生产不少于15![]() ,已知生产甲产品1
,已知生产甲产品1![]() 需煤9
需煤9![]() ,电力4
,电力4![]() ,劳力3个(按工作日计算);生产乙产品1
,劳力3个(按工作日计算);生产乙产品1![]() 需煤4
需煤4![]() ,电力5
,电力5![]() ,劳力10个;甲产品每吨价7万元,乙产品每吨价12万元;但每天用煤最不得超过300吨,电力不得超过200
,劳力10个;甲产品每吨价7万元,乙产品每吨价12万元;但每天用煤最不得超过300吨,电力不得超过200![]() ,劳力只有300个.问每天各生产甲、乙两种产品多少
,劳力只有300个.问每天各生产甲、乙两种产品多少![]() ,才能既保定完成生产任务,又能为国家创造最多的财富.
,才能既保定完成生产任务,又能为国家创造最多的财富.
分析:先设每天生产甲、乙两种产品的产量分别为![]() 和
和![]() ,建立约束条件和目标函数后,再利用图形直观解题.
,建立约束条件和目标函数后,再利用图形直观解题.
解:设每天生产甲产品![]() ,乙产品
,乙产品![]() ,总产值
,总产值![]() ,依题意约束条件为:
,依题意约束条件为:
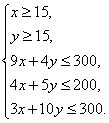
目标函数为![]() .
.
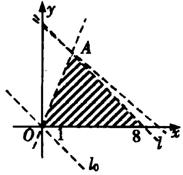
约束条件表示的可行域是五条直线所围成区域的内部的点加上它的边线上的点(如图阴影部分).
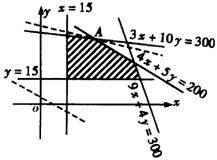
现在就要在可行域上找出使![]() 取最大值的点
取最大值的点![]() .作直线
.作直线![]() ,随着
,随着![]() 取值的变化,得到一束平行直线,其纵截距为
取值的变化,得到一束平行直线,其纵截距为![]() ,可以看出,当直线的纵截距越大,
,可以看出,当直线的纵截距越大,![]() 值也越大.
值也越大.
从图中可以看出,当直线![]() 经过点
经过点![]() 时,直线的纵截距最大,所以
时,直线的纵截距最大,所以![]() 也取最大值.
也取最大值.
解方程组![]()
得![]() .故当
.故当![]() ,
,![]() 时,
时,
![]() (万元).
(万元).
答:第天生产甲产品20![]() ,乙产品24
,乙产品24![]() ,这样既保证完成任务,又能为国家创造最多的财富428万元.
,这样既保证完成任务,又能为国家创造最多的财富428万元.
说明:解决简单线性规划应用题的关键是:(1)找出线性约束条件和目标函数;(2)准确画出可行域;(3)利用![]() 的几何意义,求出最优解.如本例中,
的几何意义,求出最优解.如本例中,![]() 是目标函数
是目标函数![]() 的纵截距.
的纵截距.
典型例题十三
例13 有一批钢管,长度都是4000![]() ,要截成500
,要截成500![]() 和600
和600![]() 两种毛坯,且这两种毛坯数量比大于
两种毛坯,且这两种毛坯数量比大于![]() 配套,怎样截最合理?
配套,怎样截最合理?
分析:先设出未知数,建立约束条件和目标函数后,再按求最优解是整数解的方法去求.
解:设截500![]() 的
的![]() 根,600
根,600![]() 的
的![]() 根,根据题意,得
根,根据题意,得
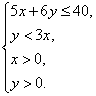 且
且![]() .
.
作出可行域,如下图中阴影部分.
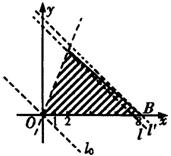
目标函数为![]() ,作一组平行直线
,作一组平行直线![]() ,经过可行域内的点且和原点距离最远的直线为过
,经过可行域内的点且和原点距离最远的直线为过![]() 的直线,这时
的直线,这时![]() .
.
由![]() ,
,![]() 为正整数,知
为正整数,知![]() 不是最优解.
不是最优解.
在可行域内找整点,使![]()
可知点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 均为最优解.
均为最优解.
答:每根钢管截500![]() 的2根,600
的2根,600![]() 的5根,或截500
的5根,或截500![]() 的3根,600
的3根,600![]() 的4根或截500
的4根或截500![]() 的4根,600
的4根,600![]() 的3根或截500
的3根或截500![]() 的5根,600
的5根,600![]() 的2根或截500
的2根或截500![]() 的6根,600
的6根,600![]() 的1根最合理.
的1根最合理.
说明:本题易出现如下错解:设截500![]() 的
的![]() 根,600
根,600![]() 的
的![]() 根,则
根,则
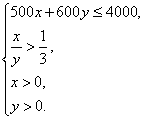 即
即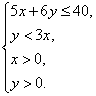
其中![]() 、
、![]() 均为整数.作出可行域,如下图所示中阴影部分.目标函数为
均为整数.作出可行域,如下图所示中阴影部分.目标函数为![]() ,作一组平行直线
,作一组平行直线![]() ,经过可行域内的点且和原点相距最远的直线为过
,经过可行域内的点且和原点相距最远的直线为过![]() 点的直线.先求
点的直线.先求![]() 点的坐标,
点的坐标,
解![]() 得
得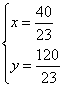 ,
,
故![]() ,即
,即![]() ,调整为
,调整为![]() ,
,![]() .
.
经检验满足条件,所以每根截500![]() 的2根,600
的2根,600![]() 的5根最合理.
的5根最合理.
本题解法错误主要是在作一组平行直线![]() 时没能准确作出,而得到经过可行域内的点且和原点距离最远的直线为过
时没能准确作出,而得到经过可行域内的点且和原点距离最远的直线为过![]() 点的直线.
点的直线.
此错误可检验如下:
如果直线![]() 通过
通过![]() 点,它是经过可行域内的点且到原点距离最远的直线,那么
点,它是经过可行域内的点且到原点距离最远的直线,那么![]() ,即
,即![]() .由于
.由于![]() ,
,![]() 为整数,所以点
为整数,所以点![]() 不是最优解但在可行域内除
不是最优解但在可行域内除![]() 点外,不可能再有其他点满足
点外,不可能再有其他点满足![]() ,只能在可行域内找满足
,只能在可行域内找满足![]() 的点.如果还没有整数点,则只能在可行域内找满足
的点.如果还没有整数点,则只能在可行域内找满足![]() 的整数点.但我们知道
的整数点.但我们知道![]() ,
,![]() 满足题意,这样,就出现了矛盾,从而判断解法错误,即
满足题意,这样,就出现了矛盾,从而判断解法错误,即![]() 通过
通过![]() 点的直线并不是通过可行域内的点且和原点距离最远的直线.
点的直线并不是通过可行域内的点且和原点距离最远的直线.
典型例题十四
例14 某工厂生产![]() 、
、![]() 两种产品,已知生产
两种产品,已知生产![]() 产品1
产品1![]() 要用煤9
要用煤9![]() ,电力4
,电力4![]() ,3个工作日;生产
,3个工作日;生产![]() 产品1
产品1![]() 要用煤4
要用煤4![]() ,电力5
,电力5![]() ,10个工作日.又知生产出
,10个工作日.又知生产出![]() 产品1
产品1![]() 可获利7万元,生产出
可获利7万元,生产出![]() 产品1
产品1![]() 可获利12万元,现在工厂只有煤360
可获利12万元,现在工厂只有煤360![]() ,电力200
,电力200![]() ,300个工作日,在这种情况下生产
,300个工作日,在这种情况下生产![]() ,
,![]() 产品各多少千克能获得最大经济效益.
产品各多少千克能获得最大经济效益.
分析:在题目条件比较复杂时,可将题目中的条件列表.
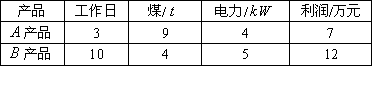
解:设这个工厂应分别生产![]() ,
,![]() 产品
产品![]() ,
,![]() ,可获利
,可获利![]() 万元.根据上表中的条件,列出线性约束条件为
万元.根据上表中的条件,列出线性约束条件为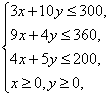 目标函数为
目标函数为![]() (万元).
(万元).
画出如图所示的可行域,做直线![]() ,做一组直线
,做一组直线![]() 与
与![]() 平行,当
平行,当![]() 过点
过点![]() 时
时![]() 最大.由
最大.由![]() 得
得![]() 点坐标为
点坐标为![]() .把
.把![]() 点坐标代入
点坐标代入![]() 的方程,得
的方程,得![]() (万元).
(万元).
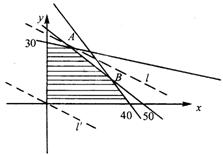
答:应生产![]() 产品20
产品20![]() ,
,![]() 产品24
产品24![]() ,能获最大利润428万元.
,能获最大利润428万元.
说明:把实际问题转化为线性规划问题的难点在于找出题目中的所有线性约束条件.同时本题的可行域形状较复杂,要注意分析目标函数的斜率和各边界斜率的关系:从而确定在何处取得最优解.解应用题时还应注意设出未知量和做答这两个必要步骤.
典型例题十五
例15 某公司每天至少要运送180![]() 货物.公司有8辆载重为6
货物.公司有8辆载重为6![]() 的
的![]() 型卡车和4辆载重为10
型卡车和4辆载重为10![]() 的
的![]() 型卡车,
型卡车,![]() 型卡车每天可往返4次,
型卡车每天可往返4次,![]() 型卡车可往返3次,
型卡车可往返3次,![]() 型卡车每天花费320元,
型卡车每天花费320元,![]() 型卡车每天花费504元,问如何调配车辆才能使公司每天花费最少.
型卡车每天花费504元,问如何调配车辆才能使公司每天花费最少.
分析:设![]() 型卡车
型卡车![]() 辆,
辆,![]() 型卡车
型卡车![]() 辆.问题转化为线性规划问题.同时应注意到题中的
辆.问题转化为线性规划问题.同时应注意到题中的![]() ,
,![]() 只能取整数.
只能取整数.
解:设![]() 型卡车
型卡车![]() 辆,
辆,![]() 型卡车
型卡车![]() 辆,则
辆,则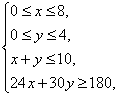 即
即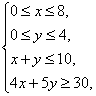
目标函数![]() .做如图所示的可行域,
.做如图所示的可行域,
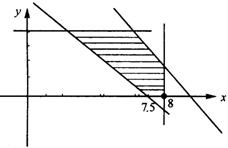
做直线![]() .在可行域中打上网格,找出
.在可行域中打上网格,找出![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…等整数点.做
,…等整数点.做![]() 与
与![]() 平行,可见当
平行,可见当![]() 过
过![]() 时
时![]() 最小,即
最小,即![]() (元).
(元).
说明:整数解的线性规划问题.如果取最小值时不是整数点,则考虑此点附近的整数点.
典型例题十六
例16 某工厂利用两种燃料生产三种不同的产品![]() 、
、![]() 、
、![]() ,每消耗一吨燃料与产品
,每消耗一吨燃料与产品![]() 、
、![]() 、
、![]() 有下列关系:
有下列关系:
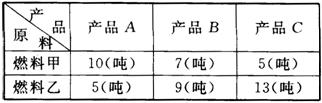
现知每吨燃料甲与燃料乙的价格之比为![]() ,现需要三种产品
,现需要三种产品![]() 、
、![]() 、
、![]() 各50吨、63吨、65吨.问如何使用两种燃料,才能使该厂成本最低?
各50吨、63吨、65吨.问如何使用两种燃料,才能使该厂成本最低?
分析:由于该厂成本与两种燃料使用量有关,而产品![]() 、
、![]() 、
、![]() 又与这两种燃料有关,且这三种产品的产量也有限制,因此这是一道求线性目标函数在线性约束条件下的最小值问题,这类简单的线性规划问题一般都可以利用二元一次不等式求在可行域上的最优解.
又与这两种燃料有关,且这三种产品的产量也有限制,因此这是一道求线性目标函数在线性约束条件下的最小值问题,这类简单的线性规划问题一般都可以利用二元一次不等式求在可行域上的最优解.
解:设该厂使用燃料甲![]() 吨,燃料乙
吨,燃料乙![]() 吨,甲每吨
吨,甲每吨![]() 元,
元,
则成本为![]() .因此只须求
.因此只须求![]() 的最小值即可.
的最小值即可.
又由题意可得![]() 、
、![]() 满足条件
满足条件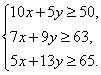
作出不等式组所表示的平面区域(如图)
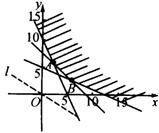
由![]() 得
得![]()
由![]() 得
得![]()
作直线![]() ,把直线
,把直线![]() 向右上方平移至可行域中的点
向右上方平移至可行域中的点![]() 时,
时,
![]() .
.
∴最小成本为![]() .
.
答:应用燃料甲![]() 吨,燃料乙
吨,燃料乙![]() 吨,才能使成本最低.
吨,才能使成本最低.
说明:本题中燃料的使用不需要是整数吨,若有些实际应用问题中的解是整数解,又该如何来考虑呢?
典型例题十七
例17 咖啡馆配制两种饮料,甲种饮料每杯含奶粉9克、咖啡4克、糖3克,乙种饮料每杯含奶粉4克、咖啡5克、糖10克.已知每天原料的使用限额为奶粉3600克、咖啡2000克、糖3000克.如果甲种饮料每杯能获利0.7元,乙种饮料每杯能获利1.2元,每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
分析:这是一道线性规划的应用题,求解的困难在于从实际问题中抽象出不等式组.只要能正确地抽象出不等式组,即可得到正确的答案.
解:设每天配制甲各饮料![]() 杯、乙种饮料
杯、乙种饮料![]() 杯可获得最大利润,利润总额为
杯可获得最大利润,利润总额为![]() 元.
元.
由条件知:![]() .变量
.变量![]() 、
、![]() 满足
满足
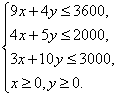
作出不等式组所表示的可行域(如图)
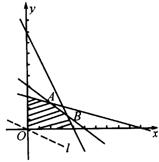
作直线![]() ,把直线
,把直线![]() 向右上方平移至经过
向右上方平移至经过![]() 点的位置时,
点的位置时,![]() 取最大值.
取最大值.
由方程组:![]()
得![]() 点坐标
点坐标![]() .
.
答:应每天配制甲种饮料200杯,乙种饮料240杯方可获利最大.