典型例题一
例1 比较![]() 与
与![]() 的大小,其中
的大小,其中![]() .
.
解:![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴
![]() .
.
说明:由例1可以看出实数比较大小的依据是:①![]() ;
;
②![]() ;③
;③![]() .
.
典型例题二
例2 比较![]() 与
与![]() 的大小,其中
的大小,其中![]()
解:![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
∴
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]()
说明:两个实数比较大小,通常用作差法来进行,其一般步骤是:第一步:作差;第二步:变形,常采用配方,因式分解等恒等变形手段;第三步:定号,贵州省是能确定是大于0,还是等于0,还是小于0.最后得结论.概括为“三步,—结论”,这里的“变形”一步最为关键.
典型例题三
例3 ![]() ,比较
,比较![]() 与
与![]() (
(![]() )的大小.
)的大小.
分析:直接作差需要将![]() 与
与![]() (
(![]() )展开,过程复杂,式子冗长,可否考虑根据两个式子特点,予以变形,再作差.
)展开,过程复杂,式子冗长,可否考虑根据两个式子特点,予以变形,再作差.
解:∵![]() =
=![]() (
(![]() )
)
![]() ,
,
![]()
![]() ,
,
∴
![]()
![]() .
.
则有![]() 时,
时,![]()
![]()
![]() (
(![]() )恒成立.
)恒成立.
说明:有的确问题直接作差不容易判断其符号,这时可根据两式的特点考虑先变形,到比较易于判断符号时,再作差,予以比较,如此例就是先变形后,再作差.
典型例题四
例4 设![]() ,比较
,比较![]() 与
与![]() 的大小.
的大小.
解:作差![]() ,
,
1)当![]() 时,即
时,即![]() ,
,
∴
![]() ;
;
2)当![]() ,即
,即![]() 时,
时,![]() ,
,
∴![]() ;
;
3)当![]() 但
但![]() ,即
,即![]() 或
或![]() 时,
时,![]() ,
,
∴![]() .
.
说明:如本题作差,变形,变形到最简形式时,由于式中含有字母,不能定号,必须对字母根据式子具体特点分类讨论才能定号.此时要注意分类合理恰当.
典型例题五
例5 比较![]() 与
与![]() 的大小
的大小
分析:两个数是幂的形式,比较大小一般采用作商法。
解:![]()
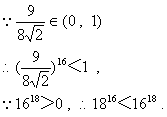
说明:求商法比大小的变形要围绕与1比大小进行.
典型例题六
例6 设![]() ,且
,且![]() ,比较:
,比较:![]() 与
与![]() 的大小。
的大小。
分析:比较大小一般方法是求差法或求商法,利用不等式的性质进行变形,然后确定大小。
解:![]()
当![]() 时,
时,![]() ,
,![]()
当![]() 时,
时,![]()
![]()
![]() 即
即![]() ,
,
又![]() ,
,![]()
说明:求商法的基本步骤是:①求商,②变形,③与1比大小从而确定两个数的大小.
典型例题七
例7 实数![]() 满足条件:①
满足条件:①![]() ;②
;②![]() ;③
;③![]() ,则有( )
,则有( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
(天津市2001年南开中学期末试题)
分析:先由条件②③分析出![]() 与
与![]() 的关系,根据条件利用①用数轴数形结合比出大小.
的关系,根据条件利用①用数轴数形结合比出大小.
解:∵![]() ,∴
,∴![]() 与
与![]() 同侧
同侧
∵![]() ,∴
,∴![]() 与
与![]() 异侧
异侧
∵![]()
∴把![]() 标在数轴上,只有下面一种情况
标在数轴上,只有下面一种情况
![]()
由此得出![]() ,∴此题选D.
,∴此题选D.
说明:比较大小时可以借助于数轴,利用推出的一些结论在数轴上标出它们的相对位置,这样容易看出几个数之间的大小关系,尤其是比较的个数较多时适用.
典型例题八
例8 已知①![]() ;②
;②![]() ,求:
,求:![]() 的取值范围.
的取值范围.
分析:此题是给代数式的字母的范围,求另外代数式的范围.分为两步来进行:(1)利用待定系数法将代数式![]() 用
用![]() 和
和![]() 表示.(2)利用不等式性质及题目条件确定
表示.(2)利用不等式性质及题目条件确定![]() 的范围.
的范围.
解:设:![]()
![]()
由①+②×2得:![]()
![]() :
:![]() .
.
说明:此题的一种典型错误做法,如下:
![]()
![]() ,即:
,即:![]()
![]()
![]() :
:![]()
![]()
此解法的错误原因是因为![]() 与
与![]() 是两个相互联系,相互制约的量,而不是各自独立的,当
是两个相互联系,相互制约的量,而不是各自独立的,当![]() 取到最大值或最小值时,
取到最大值或最小值时,![]() 不一定能取到最值,所以用以上方法可能扩大变量的范围.
不一定能取到最值,所以用以上方法可能扩大变量的范围.
避免出错的方法是通过待定系数法“整体代入”,见解题过程.
典型例题九
例9 判断下列各命题的真假,并说明理由.
(1)若![]() ,则
,则![]()
(2)若![]() ,则
,则![]()
(3)若![]() ,则
,则![]()
(4)若![]() ,则
,则![]()
(5)若![]() ,则
,则![]()
(6)若![]() ,则
,则![]()
分析:利用不等式的性质来判断命题的真假.
解:(1)![]()
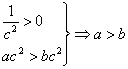 ,是真命题.
,是真命题.
(2)可用赋值法:![]() ,有
,有![]() ,是假命题.
,是假命题.
也可这样说明:![]() ,
,
∵ ![]() ,只能确定
,只能确定![]() ,
,
但![]() 的符号无法确定,从而
的符号无法确定,从而![]() 的符号确定不了,所以
的符号确定不了,所以![]() 无法得到,实际上有:
无法得到,实际上有:
![]()
![]()
(3)与(2)类似,由![]()
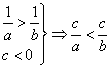 ,从而
,从而![]() 是假命题.
是假命题.
(4)取特殊值:![]()
有![]() ,∴ 是假命题.
,∴ 是假命题.
定理3的推论是同向不等式可相加,但同向不等式相减不一定成立.只有异向不等式可相减,即![]()
(5)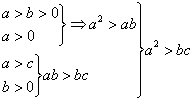 , ∴是真命题.
, ∴是真命题.
(6)定理4成立的条件为必须是正数.
举反例:
![]() ,则有
,则有![]()
说明:在利用不等式的性质解题时,一定要注意性质定理成立的条件.要说明一个命题是假命题可通过举反例.
典型例题十
例10 求证:![]()
分析:把已知的大小关系转化为差数的正负,再利用不等式的性质完成推理.
证明:利用不等式的性质,得
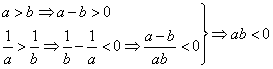
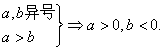
典型例题十一
例11 若![]() ,则下面不等式中成立的一个是( )
,则下面不等式中成立的一个是( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
解:由不等式的性质知:(A)、(B)、(C)成立的条件都不充分,所以选(D),其实(D) 正是异向不等式相减的结果.
![]()
说明:本的解法都是不等式性质的基本应用,对于不等式的基本性质要逐条掌握准确,以便灵活应用.
典型例题十二
例12 若![]() ,则下面各式中恒成立的是( ).
,则下面各式中恒成立的是( ).
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
分析 本题考查是否能正确使用不等式的性质来进行变形,应看到,已知条件中含有两个内容,即![]() ,
,![]() 和
和![]() ,根据不等式的性质,可得
,根据不等式的性质,可得![]() ,
,![]() ,继而得到
,继而得到![]() 且
且![]() ,故
,故![]() ,因此选A.
,因此选A.
典型例题十三
例13 若![]() ,则一定成立的不等式是( )
,则一定成立的不等式是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
分析:A错,当![]() 时有
时有![]() ;同样B错;D没有考虑各数取零和正负号的关系,所以也不对.
;同样B错;D没有考虑各数取零和正负号的关系,所以也不对.
故选C,因为不等式两边同时加上一个任意数(此题是![]() ),原不等式成立.
),原不等式成立.
说明:这类题可以采用特例法:令![]() 即得C成立.
即得C成立.
典型例题十四
例14 已知:![]() ,求证:
,求证:![]() .
.
分析:要证明的式子中,左右均为二项差,其中都有一项是两字母积的形式,因此在证明时,对两项积要注意性质的使用,对两项差的证明要注意使用同向加性或异向减性来处理.
证明:![]()
![]()
又![]() ∴由同向加性可得:
∴由同向加性可得:![]() .
.
说明:此题还可采用异向减性来处理:![]() 做这类题过程并不复杂,关键是记准性质,并能正确地应用.
做这类题过程并不复杂,关键是记准性质,并能正确地应用.
典型例题十五
例15已知集合![]() 求:
求:![]() .
.
分析:要求![]() ,需要先求集合
,需要先求集合![]() 和
和![]() ,从已知来看,
,从已知来看,![]() 的范围容易求,
的范围容易求,![]() 的元素由
的元素由![]() 可以推算,但在推算过程中,要注意运用不等式的性质.
可以推算,但在推算过程中,要注意运用不等式的性质.
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
说明:本题中的条件![]() ,意在明确集合
,意在明确集合![]() 中的元素为
中的元素为![]() ,若去掉此条件,会出现不确定的情况.比如,
,若去掉此条件,会出现不确定的情况.比如,![]() 的实数和
的实数和![]() 的整数显然是有区别的.另外,这里集合
的整数显然是有区别的.另外,这里集合![]() 的元素是通过集合
的元素是通过集合![]() 的元素求出的,解题时,一定要看清.
的元素求出的,解题时,一定要看清.
典型例题十六
例16 设![]() 和
和![]() 都是非零实数,求不等式
都是非零实数,求不等式![]() 和
和![]() 同时成立的充要条件.
同时成立的充要条件.
分析:本题是求两个不等式同时成立的充要条件,因此,这两个不等式不能分开来讨论.如果分开讨论,则![]() 成立的条件就是
成立的条件就是![]() 本身;而
本身;而![]() 成立的条件则是
成立的条件则是![]() 与
与![]() 同号,且
同号,且![]() ,但这个条件只是
,但这个条件只是![]() 的一个充分条件,并且与第一个不等式
的一个充分条件,并且与第一个不等式![]() 是矛盾的.所以必须研究这两个不等式同时成立的条件.显然,应该从求它们同时成立的必要条件入手.
是矛盾的.所以必须研究这两个不等式同时成立的条件.显然,应该从求它们同时成立的必要条件入手.
解:先求![]() ,
,![]() 同时成立的必要条件,即当
同时成立的必要条件,即当![]() ,
,![]() 同时成立时,
同时成立时,![]() 与
与![]() 应具备什么条件.
应具备什么条件.
由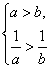 ,得
,得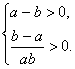
由![]() 可知
可知![]() ,再由
,再由![]() 知
知![]() ,即
,即![]() 与
与![]() 异号,因此
异号,因此![]() 是不等式
是不等式![]() 与
与![]() 同时成立的必要条件.
同时成立的必要条件.
再求![]() ,
,![]() 同时成立的充分条件.
同时成立的充分条件.
事实上,当![]() 时,必有
时,必有![]() ,且
,且![]() ,因而
,因而![]() 成立.从而
成立.从而![]() 是不等式
是不等式![]() ,
,![]() 同时成立的充分条件.
同时成立的充分条件.
因此,两个不等式![]() ,
,![]() 同时成立的充要条件是
同时成立的充要条件是![]() .
.
说明:本题结果表明,![]() 与
与![]() 同时成立,其充要条件是
同时成立,其充要条件是![]() 为正数,
为正数,![]() 为负数.这与
为负数.这与![]() 成立的条件
成立的条件![]() ,
,![]() 不要混淆.解本题是从必要条件入手的,即若
不要混淆.解本题是从必要条件入手的,即若![]() ,
,![]() 同时成立,则要研究从不等式
同时成立,则要研究从不等式![]() 和
和![]() 看
看![]() 与
与![]() 的大小有什么关系,从中得出结论(
的大小有什么关系,从中得出结论(![]() ),再把这个结论作为一个充分条件去验证
),再把这个结论作为一个充分条件去验证![]() 及
及![]() 能否同时成立.从而解决了本题.
能否同时成立.从而解决了本题.
典型例题十七
例17 已知函数![]() 满足:
满足:![]() 则
则![]() 应满足( )
应满足( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
分析:如果能用![]() 与
与![]() 将
将![]() “线性”表示出:
“线性”表示出:![]() ,就可利用不等式的基本性质,由
,就可利用不等式的基本性质,由![]() 、
、![]() 的取值范围,推出
的取值范围,推出![]() 满足的条件.
满足的条件.
解:∵![]()
∴![]()
故![]()
![]()
由不等式的基本性质,得
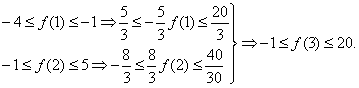
故选(C).
说明:(1)也可设![]() ,由代定系数法求得
,由代定系数法求得![]() ,
,![]() .
.
(2)下面的错误是值得引以为戒的∵![]()
![]()
![]()
又 ![]()
∴ ![]()
故选(A)
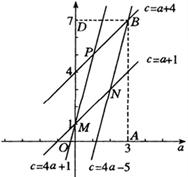 上述推理错误产生的原因是由于将条件
上述推理错误产生的原因是由于将条件
![]() 化为
化为![]() 使
使![]() 、
、![]() 的取值范围扩大所致.事实上,作为点集
的取值范围扩大所致.事实上,作为点集
![]()
与![]() 之间的关系是
之间的关系是![]() ,如图点集N是图中乱世形OABD所围成的区域,点集M是由平行四边形MNBP所围成的区域,这样就直观地表现了
,如图点集N是图中乱世形OABD所围成的区域,点集M是由平行四边形MNBP所围成的区域,这样就直观地表现了![]() ,揭示了上述解法的错误.
,揭示了上述解法的错误.