典型例题一
例1 解不等式:(1)![]() ;(2)
;(2)![]() .
.
分析:如果多项式![]() 可分解为
可分解为![]() 个一次式的积,则一元高次不等式
个一次式的积,则一元高次不等式![]() (或
(或![]() )可用“穿根法”求解,但要注意处理好有重根的情况.
)可用“穿根法”求解,但要注意处理好有重根的情况.
解:(1)原不等式可化为
![]()
把方程![]() 的三个根
的三个根![]() 顺次标上数轴.然后从右上开始画线顺次经过三个根,其解集如下图的阴影部分.
顺次标上数轴.然后从右上开始画线顺次经过三个根,其解集如下图的阴影部分.
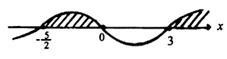
∴原不等式解集为![]()
(2)原不等式等价于
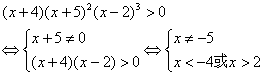
∴原不等式解集为![]()
说明:用“穿根法”解不等式时应注意:①各一次项中![]() 的系数必为正;②对于偶次或奇次重根可转化为不含重根的不等式,也可直接用“穿根法”,但注意“奇穿偶不穿”,其法如下图.
的系数必为正;②对于偶次或奇次重根可转化为不含重根的不等式,也可直接用“穿根法”,但注意“奇穿偶不穿”,其法如下图.

典型例题二
例2 解下列分式不等式:
(1)![]() ; (2)
; (2)![]()
分析:当分式不等式化为![]() 时,要注意它的等价变形
时,要注意它的等价变形
①![]()
②![]()
![]()
(1)解:原不等式等价于
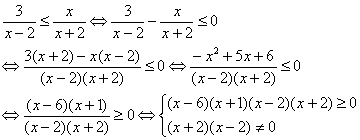
用“穿根法”
∴原不等式解集为![]() 。
。
(2)解法一:原不等式等价于 ![]()
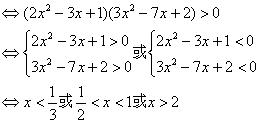
∴原不等式解集为![]() 。
。
![]()
解法二:原不等式等价于![]()
![]()
用“穿根法”
∴原不等式解集为![]()
典型例题三
例3 解不等式![]()
分析:解此题的关键是去绝对值符号,而去绝对值符号有两种方法:一是根据绝对值的意义![]()
二是根据绝对值的性质:![]() 或
或![]() ,因此本题有如下两种解法.
,因此本题有如下两种解法.
解法一:原不等式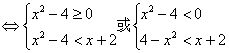
即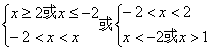
∴![]() 或
或![]()
故原不等式的解集为![]() .
.
解法二:原不等式等价于 ![]()
即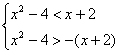 ∴
∴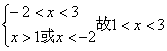 .
.
典型例题四
例4 解不等式![]() .
.
分析:这是一个分式不等式,其左边是两个关于![]() 二次式的商,由商的符号法则,它等价于下列两个不等式组:
二次式的商,由商的符号法则,它等价于下列两个不等式组:
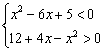 或
或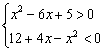
所以,原不等式的解集是上面两个不等式级的解集的并集.也可用数轴标根法求解.
解法一:原不等式等价下面两个不等式级的并集:
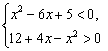 或
或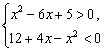
![]() 或
或![]()
![]() 或
或![]()
![]() 或
或![]() 或
或![]() .
.
∴原不等式解集是![]() .
.
解法二:原不等式化为![]() .
.
画数轴,找因式根,分区间,定符号.
![]() 符号
符号
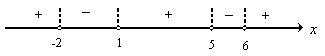
∴原不等式解集是![]() .
.
说明:解法一要注意求两个等价不等式组的解集是求每组两个不等式的交集,再求两组的解的并集,否则会产生误解.
解法二中,“定符号”是关键.当每个因式![]() 的系数为正值时,最右边区间一定是正值,其他各区间正负相间;也可以先决定含0的区间符号,其他各区间正负相间.在解题时要正确运用.
的系数为正值时,最右边区间一定是正值,其他各区间正负相间;也可以先决定含0的区间符号,其他各区间正负相间.在解题时要正确运用.
典型例题五
例5 解不等式![]() .
.
分析:不等式左右两边都是含有![]() 的代数式,必须先把它们移到一边,使另一边为0再解.
的代数式,必须先把它们移到一边,使另一边为0再解.
解:移项整理,将原不等式化为![]() .
.
由![]() 恒成立,知原不等式等价于
恒成立,知原不等式等价于![]() .
.
解之,得原不等式的解集为![]() .
.
说明:此题易出现去分母得![]() 的错误解法.避免误解的方法是移项使一边为0再解.
的错误解法.避免误解的方法是移项使一边为0再解.
另外,在解题过程中,对出现的二项式要注意其是否有实根,以便分析不等式是否有解,从而使求解过程科学合理.
典型例题六
例6 设![]() ,解关于
,解关于![]() 的不等式
的不等式![]() .
.
分析:进行分类讨论求解.
解:当![]() 时,因
时,因![]() 一定成立,故原不等式的解集为
一定成立,故原不等式的解集为![]() .
.
当![]() 时,原不等式化为
时,原不等式化为![]() ;
;
当![]() 时,解得
时,解得![]() ;
;
当![]() 时,解得
时,解得![]() .
.
∴当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() .
.
说明:解不等式时,由于![]() ,因此不能完全按一元二次不等式的解法求解.因为当
,因此不能完全按一元二次不等式的解法求解.因为当![]() 时,原不等式化为
时,原不等式化为![]() ,此时不等式的解集为
,此时不等式的解集为![]() ,所以解题时应分
,所以解题时应分![]() 与
与![]() 两种情况来讨论.
两种情况来讨论.
在解出![]() 的两根为
的两根为![]() ,
,![]() 后,认为
后,认为![]() ,这也是易出现的错误之处.这时也应分情况来讨论:当
,这也是易出现的错误之处.这时也应分情况来讨论:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
典型例题七
例7 解关于![]() 的不等式
的不等式![]() .
.
分析:先按无理不等式的解法化为两个不等式组,然后分类讨论求解.
解:原不等式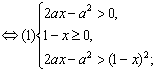 或
或![]()
由![]() ,得:
,得: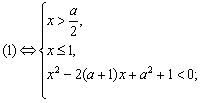
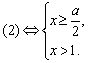
由判别式![]() ,故不等式
,故不等式![]() 的解是
的解是![]() .
.
当![]() 时,
时,![]() ,
,![]() ,不等式组(1)的解是
,不等式组(1)的解是![]() ,不等式组(2)的解是
,不等式组(2)的解是![]() .
.
当![]() 时,不等式组(1)无解,(2)的解是
时,不等式组(1)无解,(2)的解是![]() .
.
综上可知,当![]() 时,原不等式的解集是
时,原不等式的解集是![]() ;当
;当![]() 时,原不等式的解集是
时,原不等式的解集是![]() .
.
说明:本题分类讨论标准“![]() ,
,![]() ”是依据“已知
”是依据“已知![]() 及(1)中‘
及(1)中‘![]() ,
,![]() ’,(2)中‘
’,(2)中‘![]() ,
,![]() ’”确定的.解含有参数的不等式是不等式问题中的难点,也是近几年高考的热点.一般地,分类讨论标准(解不等式)大多数情况下依“不等式组中的各不等式的解所对应的区间的端点”去确定.
’”确定的.解含有参数的不等式是不等式问题中的难点,也是近几年高考的热点.一般地,分类讨论标准(解不等式)大多数情况下依“不等式组中的各不等式的解所对应的区间的端点”去确定.
本题易误把原不等式等价于不等式![]() .纠正错误的办法是熟练掌握无理不等式基本类型的解法.
.纠正错误的办法是熟练掌握无理不等式基本类型的解法.
典型例题八
例8 解不等式![]() .
.
分析:先去掉绝对值号,再找它的等价组并求各不等式的解,然后取它们的交集即可.
解答:去掉绝对值号得![]() ,
,
∴原不等式等价于不等式组
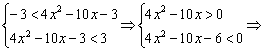
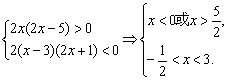
∴原不等式的解集为![]() .
.
说明:解含绝对值的不等式,关键是要把它化为不含绝对值的不等式,然后把不等式等价转化为不等式组,变成求不等式组的解.
典型例题九
例9 解关于![]() 的不等式
的不等式![]() .
.
分析:不等式中含有字母![]() ,故需分类讨论.但解题思路与一般的一元二次不等式的解法完全一样:求出方程
,故需分类讨论.但解题思路与一般的一元二次不等式的解法完全一样:求出方程![]() 的根,然后写出不等式的解,但由于方程的根含有字母
的根,然后写出不等式的解,但由于方程的根含有字母![]() ,故需比较两根的大小,从而引出讨论.
,故需比较两根的大小,从而引出讨论.
解:原不等式可化为![]() .
.
(1)当![]() (即
(即![]() 或
或![]() )时,不等式的解集为:
)时,不等式的解集为:
![]() ;
;
(2)当![]() (即
(即![]() )时,不等式的解集为:
)时,不等式的解集为:
![]() ;
;
(3)当![]() (即
(即![]() 或1)时,不等式的解集为:
或1)时,不等式的解集为:
![]() .
.
说明:对参数进行的讨论,是根据解题的需要而自然引出的,并非一开始就对参数加以分类、讨论.比如本题,为求不等式的解,需先求出方程的根![]() ,
,![]() ,因此不等式的解就是
,因此不等式的解就是![]() 小于小根或
小于小根或![]() 大于大根.但
大于大根.但![]() 与
与![]() 两根的大小不能确定,因此需要讨论
两根的大小不能确定,因此需要讨论![]() ,
,![]() ,
,![]() 三种情况.
三种情况.
典型例题十
例10 已知不等式![]() 的解集是
的解集是![]() .求不等式
.求不等式![]() 的解集.
的解集.
分析:按照一元二次不等式的一般解法,先确定系数![]() 的正负,然后求出方程
的正负,然后求出方程![]() 的两根即可解之.
的两根即可解之.
解:(解法1)由题可判断出![]() ,
,![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ,
,![]() .
.
又![]() 的解集是
的解集是![]() ,说明
,说明![]() .
.
而![]() ,
,![]()
![]() ,
,
∴![]() .
.
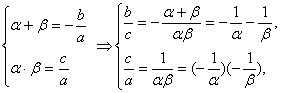
∴![]() ,即
,即![]() ,
,
即![]() .
.
又![]() ,∴
,∴![]() ,
,
∴![]() 的解集为
的解集为![]() .
.
(解法2)由题意可判断出![]() ,
,![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() .
.
又![]() 的解集是
的解集是![]() ,说明
,说明![]() .
.
而![]() ,
,![]()
![]() .
.
对方程![]() 两边同除以
两边同除以![]() 得
得
![]() .
.
令![]() ,该方程即为
,该方程即为
![]() ,它的两根为
,它的两根为![]() ,
,![]() ,
,
∴![]() ,
,![]() .∴
.∴![]() ,
,![]() ,
,
∴方程![]() 的两根为
的两根为![]() ,
,![]() .
.
∵![]() ,∴
,∴![]() .
.
∴不等式![]() 的解集是
的解集是![]() .
.
说明:(1)万变不离其宗,解不等式的核心即是确定首项系数的正负,求出相应的方程的根;(2)结合使用韦达定理,本题中只有![]() ,
,![]() 是已知量,故所求不等式解集也用
是已知量,故所求不等式解集也用![]() ,
,![]() 表示,不等式系数
表示,不等式系数![]() ,
,![]() ,
,![]() 的关系也用
的关系也用![]() ,
,![]() 表示出来;(3)注意解法2中用“变换”的方法求方程的根.
表示出来;(3)注意解法2中用“变换”的方法求方程的根.
典型例题十二
例12 若不等式![]() 的解为
的解为![]() ,求
,求![]() 、
、![]() 的值.
的值.
分析:不等式本身比较复杂,要先对不等式进行同解变形,再根据解集列出关于![]() 、
、![]() 式子.
式子.
解:∵![]() ,
,
![]() ,
,
∴原不等式化为![]() .
.
依题意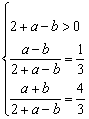 ,
,
∴![]() .
.
说明:解有关一元二次方程的不等式,要注意判断二次项系数的符号,结合韦达定理来解.
典型例题十三
例13 不等式![]() 的解集为
的解集为![]() ,求
,求![]() 与
与![]() 的值.
的值.
分析:此题为一元二次不等式逆向思维题,要使解集为![]() ,不等式
,不等式![]() 需满足条件
需满足条件![]() ,
,![]() ,
,![]() 的两根为
的两根为![]() ,
,![]() .
.
解法一:设![]() 的两根为
的两根为![]() ,
,![]() ,由韦达定理得:
,由韦达定理得:
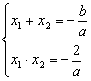 由题意:
由题意: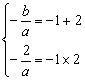
∴![]() ,
,![]() ,此时满足
,此时满足![]() ,
,![]() .
.
解法二:构造解集为![]() 的一元二次不等式:
的一元二次不等式:
![]() ,即
,即![]() ,此不等式与原不等式
,此不等式与原不等式![]() 应为同解不等式,故需满足:
应为同解不等式,故需满足:
![]() ∴
∴![]() ,
,![]() .
.
说明:本题考查一元二次方程、一元二次不等式解集的关系,同时还考查逆向思维的能力.对有关字母抽象问题,同学往往掌握得不好.
典型例题十四
例14 解关于![]() 的不等式
的不等式![]() .
.
分析:本题考查一元一次不等式与一元二次不等式的解法,因为含有字母系数,所以还考查分类思想.
解:分以下情况讨论
(1)当![]() 时,原不等式变为:
时,原不等式变为:![]() ,∴
,∴![]()
(2)当![]() 时,原不等式变为:
时,原不等式变为:![]() ①
①
①当![]() 时,①式变为
时,①式变为![]() ,∴不等式的解为
,∴不等式的解为![]() 或
或![]() .
.
②当![]() 时,①式变为
时,①式变为![]() . ②
. ②
∵![]() ,∴当
,∴当![]() 时,
时,![]() ,此时②的解为
,此时②的解为![]() .当
.当![]() 时,
时,![]() ,此时②的解为
,此时②的解为![]() .
.
说明:解本题要注意分类讨论思想的运用,关键是要找到分类的标准,就本题来说有三级分类:
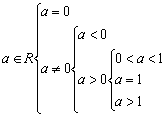
分类应做到使所给参数![]() 的集合的并集为全集,交集为空集,要做到不重不漏.另外,解本题还要注意在讨论
的集合的并集为全集,交集为空集,要做到不重不漏.另外,解本题还要注意在讨论![]() 时,解一元二次不等式
时,解一元二次不等式![]() 应首选做到将二次项系数变为正数再求解.
应首选做到将二次项系数变为正数再求解.
典型例题十五
例15 解不等式![]() .
.
分析:无理不等式转化为有理不等式,要注意平方的条件和根式有意义的条件,一般情况下,![]() 可转化为
可转化为![]() 或
或![]() ,而
,而![]() 等价于:
等价于:
![]() 或
或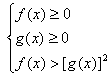 .
.
解:原不等式等价于下面两个不等式组:
①![]() ②
②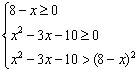
由①得![]() ,∴
,∴![]()
由②得∴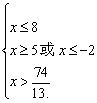
![]() ,
,
所以原不等式的解集为![]() ,即为
,即为![]() .
.
说明:本题也可以转化为![]() 型的不等式求解,注意:
型的不等式求解,注意:
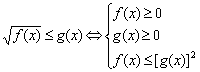 ,
,
这里,设全集![]() ,
,![]() ,
,
则所求不等式的解集为![]() 的补集
的补集![]()
![]() ,
,
由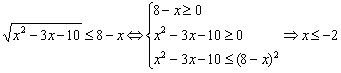 或
或![]() .
.
即![]() ,∴原不等式的解集是
,∴原不等式的解集是![]()
![]() .
.