典型例题一
例1 已知![]() ,
,![]() ,
,![]() ,求
,求![]() 点的坐标,使四边形
点的坐标,使四边形![]() 为等腰梯形.
为等腰梯形.
分析:利用等腰梯形所具备的性质“两底互相平行且两腰长相等”进行解题.
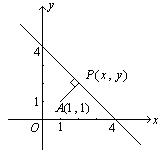
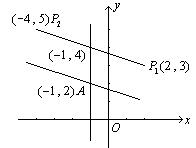
解:如图,
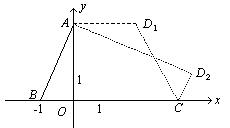
设![]() ,若
,若![]() ,则
,则![]() ,
,![]() ,
,
即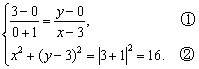
由①、②解得![]() .
.
若![]() ,则
,则![]()
即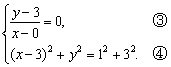
由③、④式解得![]() .
.
故![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
说明:(1)把哪两条边作为梯形的底是讨论的标准,解此题时注意不要漏解.(2)在遇到两直线平行问题时,一定要注意直线斜率不存在的情况.此题中![]() 、
、![]() 的斜率都存在,故不可能出现斜率不存在的情况.
的斜率都存在,故不可能出现斜率不存在的情况.
典型例题二
例2当![]() 为何值时,直线
为何值时,直线![]() 与直线
与直线![]() 互相垂直?
互相垂直?
分析:分类讨论,利用两直线垂直的充要条件进行求解.或利用结论“设直线![]() 和
和![]() 的方程分别是
的方程分别是![]() ,
,![]() ,则
,则![]() 的充要条件是
的充要条件是![]() ”(其证明可借助向量知识完成)解题.
”(其证明可借助向量知识完成)解题.
解法一:由题意,直线![]() .
.
(1)若![]() ,即
,即![]() ,此时直线
,此时直线![]() ,
,![]() 显然垂直;
显然垂直;
(2)若![]() ,即
,即![]() 时,直线
时,直线![]() 与直线
与直线![]() 不垂直;
不垂直;
(3)若![]() ,且
,且![]() ,则直线
,则直线![]() 、
、![]() 斜率
斜率![]() 、
、![]() 存在,
存在,
![]() ,
,![]() .
.
当![]() 时,
时,![]() ,即
,即![]() ,
,
∴![]() .
.
综上可知,当![]() 或
或![]() 时,直线
时,直线![]() .
.
解法二:由于直线![]() ,所以
,所以![]() ,解得
,解得![]() .
.
故当![]() 或
或![]() 时,直线
时,直线![]() .
.
说明:对于本题,容易出现忽视斜率存在性而引发的解题错误,如先认可两直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,则
,则![]() ,
,![]() .
.
由![]() ,得
,得![]() ,即
,即![]() .
.
解上述方程为![]() .从而得到当
.从而得到当![]() 时,直线
时,直线![]() 与
与![]() 互相垂直.
互相垂直.
上述解题的失误在于机械地套用两直线垂直(斜率形式)的充要条件,忽视了斜率存在的大前提,因而失去对另一种斜率不存在时两直线垂直的考虑,出现了以偏概全的错误.
典型例题三
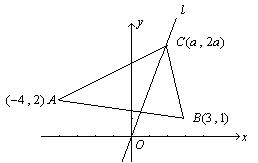
例3 已知直线![]() 经过点
经过点![]() ,且被两平行直线
,且被两平行直线![]() 和
和![]() 截得的线段之长为5,求直线
截得的线段之长为5,求直线![]() 的方程.
的方程.
分析:(1)如图,利用点斜式方程,分别与![]() 、
、![]() 联立,求得两交点
联立,求得两交点![]() 、
、![]() 的坐标(用
的坐标(用![]() 表示),再利用
表示),再利用![]() 可求出
可求出![]() 的值,从而求得
的值,从而求得![]() 的方程.(2)利用
的方程.(2)利用![]() 、
、![]() 之间的距离及
之间的距离及![]() 与
与![]() 夹角的关系求解.(3)设直线
夹角的关系求解.(3)设直线![]() 与
与![]() 、
、![]() 分别相交于
分别相交于![]() 、
、![]() ,则可通过求出
,则可通过求出![]() 、
、![]() 的值,确定直线
的值,确定直线![]() 的斜率(或倾斜角),从而求得直线
的斜率(或倾斜角),从而求得直线![]() 的方程.
的方程.
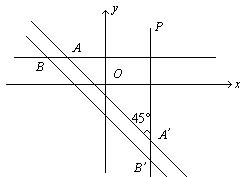
解法一:若直线![]() 的斜率不存在,则直线
的斜率不存在,则直线![]() 的方程为
的方程为![]() ,此时与
,此时与![]() 、
、![]() 的交点分别为
的交点分别为![]() 和
和![]() ,截得的线段
,截得的线段![]() 的长
的长![]() ,符合题意,
,符合题意,
若直线![]() 的斜率存在,则设直线
的斜率存在,则设直线![]() 的方程为
的方程为![]() .
.
解方程组![]() 得
得![]() ,
,
解方程组![]() 得
得![]() .
.
由![]() ,得
,得![]() .
.
解之,得![]() ,即欲求的直线方程为
,即欲求的直线方程为![]() .
.
综上可知,所求![]() 的方程为
的方程为![]() 或
或![]() .
.
解法二:由题意,直线![]() 、
、![]() 之间的距离为
之间的距离为![]() ,且直线
,且直线![]() 被平等直线
被平等直线![]() 、
、![]() 所截得的线段
所截得的线段![]() 的长为5(如上图),设直线
的长为5(如上图),设直线![]() 与直线
与直线![]() 的夹角为
的夹角为![]() ,则
,则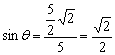 ,故∴
,故∴![]() .
.
由直线![]() 的倾斜角为135°,知直线
的倾斜角为135°,知直线![]() 的倾斜角为0°或90°,又由直线
的倾斜角为0°或90°,又由直线![]() 过点
过点![]() ,故直线
,故直线![]() 的方程为
的方程为![]() 或
或![]() .
.
解法三:设直线![]() 与
与![]() 、
、![]() 分别相交
分别相交![]() 、
、![]() ,则:
,则:
![]() ,
,![]() .
.
两式相减,得![]() . ①
. ①
又![]() ②
②
联立①、②,可得![]() 或
或![]()
由上可知,直线![]() 的倾斜角分别为0°或90°.
的倾斜角分别为0°或90°.
故所求直线方程为![]() 或
或![]() .
.
说明:本题容易产生的误解是默认直线![]() 的斜率存在,这样由解法一就只能得到
的斜率存在,这样由解法一就只能得到![]() ,从而遗漏了斜率不存在的情形.
,从而遗漏了斜率不存在的情形.
一般地,求过一定点,且被两已知平行直线截得的线段为定长![]() 的直线,当
的直线,当![]() 小于两平行直线之间距离
小于两平行直线之间距离![]() 时无解;当
时无解;当![]() 时有唯一解;当
时有唯一解;当![]() 时,有且只有两解.另外,本题的三种解法中,解法二采取先求出夹角
时,有且只有两解.另外,本题的三种解法中,解法二采取先求出夹角![]() 后,再求直线
后,再求直线![]() 的斜率或倾斜角,从方法上看较为简单;而解法三注意了利用整体思想处理问题,在一定程度上也简化了运算过程.
的斜率或倾斜角,从方法上看较为简单;而解法三注意了利用整体思想处理问题,在一定程度上也简化了运算过程.
典型例题四
例4
已知点![]() ,
,![]() ,点
,点![]() 在坐标轴上,且
在坐标轴上,且![]() ,则满足条件的点
,则满足条件的点![]() 的个数是( ).
的个数是( ).
(A)1 (B)2 (C)3 (D)4
解:点![]() 在坐标轴上,可有两种情况,即在
在坐标轴上,可有两种情况,即在![]() 轴或
轴或![]() 轴上,点
轴上,点![]() 的坐标可设为
的坐标可设为![]() 或
或![]() .
.
由题意,![]() ,直线
,直线![]() 与直线
与直线![]() 垂直,其斜率乘积为-1,可分别求得
垂直,其斜率乘积为-1,可分别求得![]() 或2,
或2,![]() 或4,所以满足条件的点的坐标为(0,0),(2,0),(0,4).
或4,所以满足条件的点的坐标为(0,0),(2,0),(0,4).
说明:①本题还可以有另外两种解法:一种是利用勾股定理,另一种是直角三角形斜边![]() 与
与![]() 轴交点
轴交点![]() 恰为斜边
恰为斜边![]() 中点,则由
中点,则由![]() 到
到![]() 、
、![]() 距离相等的性质可解.②本题易错,可能只解一个坐标轴;可能解方程时漏解;也可能看到
距离相等的性质可解.②本题易错,可能只解一个坐标轴;可能解方程时漏解;也可能看到![]() 、
、![]() 各有两解而误以为有四点.
各有两解而误以为有四点.
典型例题五
例5 已知![]() 的一个定点是
的一个定点是![]() ,
,![]() 、
、![]() 的平分线分别是
的平分线分别是![]() ,
,![]() ,求直线
,求直线![]() 的方程.
的方程.
分析:利用角平分线的轴对称性质,求出![]() 关于
关于![]() ,
,![]() 的对称点,它们显然在直线
的对称点,它们显然在直线![]() 上.
上.
解:![]() 关于
关于![]() ,
,![]() 的对称点分别是
的对称点分别是![]() 和
和![]() ,且这两点都在直线
,且这两点都在直线![]() 上,由两点式求得直线
上,由两点式求得直线![]() 方程为
方程为![]() .
.
典型例题六
例6 求经过两条直线![]() 和
和![]() 的交点,并且垂直于直线
的交点,并且垂直于直线![]() 的直线的方程.
的直线的方程.
解一:解得两直线![]() 和
和![]() 的交点为(
的交点为(![]() ,
,![]() ),由已知垂直关系可求得所求直线的斜率为
),由已知垂直关系可求得所求直线的斜率为![]() ,进而所求直线方程为
,进而所求直线方程为![]() .
.
解二:设所求直线方程为![]() ,将所求交点坐标(
,将所求交点坐标(![]() ,
,![]() )代入方程得
)代入方程得![]() ,所以所求直线方程为
,所以所求直线方程为![]() .
.
解三:所求直线过点(![]() ,
,![]() ),且与直线
),且与直线![]() 垂直,所以,所求直线方程为
垂直,所以,所求直线方程为
![]()
即
![]() .
.
解四:设所求直线得方程为
![]()
即 ![]() (1)
(1)
由于该直线与已知直线![]() 垂直
垂直
则
![]()
解得
![]()
代入(1)得所求直线方程为![]() .
.
典型例题七
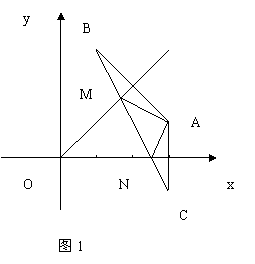
例7
已知定点![]() (3,1),在直线
(3,1),在直线![]() 和
和![]() 上分别求点
上分别求点![]() 和点
和点![]() ,使
,使![]() 的周长最短,并求出最短周长.
的周长最短,并求出最短周长.
 分析:由连接两点的线中,直线段最短,利用对称,把折线转化为直线,即转化为求两点间的距离.
分析:由连接两点的线中,直线段最短,利用对称,把折线转化为直线,即转化为求两点间的距离.
解:如图1,设点![]() 关于直线
关于直线![]() 和
和![]() 的对称点分别为
的对称点分别为![]() ,
,![]()
∵![]()
又![]()
周长最小值是: ![]()
由两点式可得![]() 方程为:
方程为:
![]() .
.
而且易求得:![]() (
(![]() ,
,![]() ),
),![]() (
(![]() ,0),
,0),
此时,周长最短,周长为![]() .
.
典型例题八
例8 已知实数![]() ,
,![]() 满足
满足![]() ,求证:
,求证:![]() .
.
解:本题的几何意义是:直线![]() 上的点(
上的点(![]() ,
,![]() )与定点
)与定点![]() 的距离的平方不小于
的距离的平方不小于![]() .因为直线外一点与直线上任一点连线中,垂线段距离最短,而垂线段的长度即距离
.因为直线外一点与直线上任一点连线中,垂线段距离最短,而垂线段的长度即距离![]() ,
,
所以![]() ,即
,即![]() .
.
说明:本题应为不等式的题目,难度较大,证明方法也较多,但用解析几何的方法解决显得轻松简捷,深刻地体现了数形结合的思想.
典型例题九
例9 在平面直角坐标系中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上
上![]() ,
,![]() ,
,![]() ,试在
,试在![]() 轴的正半周上求一点
轴的正半周上求一点![]() ,使
,使![]() 取得最大值.
取得最大值.
分析:要使最大,只需最大,而是直线到直线的角(此处即为夹角),利用公式可以解决问题.
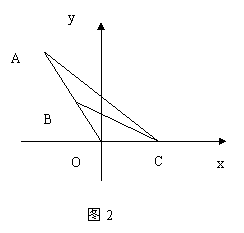 解:如图2,设点
解:如图2,设点![]()
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
于是直线![]() 、
、![]() 的斜率分别为:
的斜率分别为:
![]() ,
,
![]()
∴![]() =
=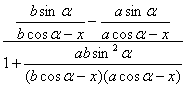
=![]()
=![]()
=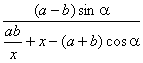
∵![]()
∴![]()
当且仅当![]() 即
即![]() ,
,![]() 点的坐标为(
点的坐标为(![]() ,0),由
,0),由![]() 可知
可知![]() 为锐角,所以此时
为锐角,所以此时![]() 有最大值
有最大值![]()
![]() .
.
说明:本题综合性强,是三角、不等式和解析几何知识的交汇点.另外本题也是足球射门最大角问题的推广.
为了更好地理解问题,可以演示用“几何画板”制作的课件.
典型例题十
例10 直线![]() ,求
,求![]() 关于直线
关于直线![]() 对称的直线
对称的直线![]() 的方程.
的方程.
分析:本题可有多种不同的解法,给出多种解法的途径是:一类利用直线方程的不同形式求解;另一类采用消元思想进行求解.
解法一:由![]() 得
得![]() 与
与![]() 的交点为
的交点为![]() ,显见
,显见![]() 也在
也在![]() 上.
上.
设![]() 的斜率为
的斜率为![]() ,又
,又![]() 的斜率为-2,
的斜率为-2,![]() 的斜率为
的斜率为![]() ,则
,则
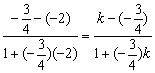 ,解得
,解得![]() .
.
故![]() 的直线方程为
的直线方程为![]() .即
.即![]() .
.
解法二:在直线![]() 上取一点
上取一点![]() ,又设点
,又设点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,则
,则
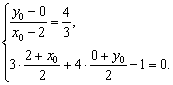 解得
解得![]()
故由两点式可求得直线![]() 的方程为
的方程为![]() .
.
解法三:设直线![]() 上一动点
上一动点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,则
,则
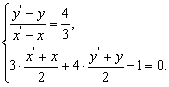
解得![]() ,
,![]() .
.
显然![]() 在
在![]() 上,即
上,即![]() ,也即
,也即![]() .这便是所求的直线
.这便是所求的直线![]() 的方程.
的方程.
解法四:设直线![]() 上一动点
上一动点![]() ,则
,则![]() 关于
关于![]() 的对称点
的对称点![]() 在直线
在直线![]() 上,可设
上,可设![]() 的坐标为
的坐标为![]() ,则
,则
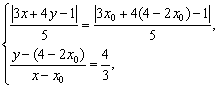
即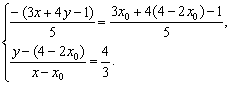
消去![]() ,得
,得![]() ,即此所求的直线
,即此所求的直线![]() 的方程.
的方程.
说明:在解法一中,应注意正确运用“到角公式”,明确由哪条直线到哪条直线的角.在具体解题时,最好能准确画出图形,直观地得出关系式.在解法四中,脱去绝对值符号时,运用了平面区域的知识.否则,若从表面上可得到两种结果,这显然很难准确地得出直线![]() 的方程.
的方程.
本题的四种不同的解法,体现了求直线方程的不同的思想方法,具有一定的综合性.除此之外,从本题的不同解法中可以看出,只有对坐标法有了充分的理解与认识,并具有较强的数形结合意识,才有可能驾驭本题,从而在解法选择的空间上,真正做到游刃有余,左右逢源.
典型例题十一
例11 不论![]() 取什么实数,直线
取什么实数,直线![]() 都经过一个定点,并求出这个定点.
都经过一个定点,并求出这个定点.
分析:题目所给的直线方程的系数含有字母![]() ,给
,给![]() 任何一个实数值,就可以得到一条确定的直线,因此所给的方程是以
任何一个实数值,就可以得到一条确定的直线,因此所给的方程是以![]() 为参数的直线系方程.要证明这个直线系的直线都过一定点,就是证明它是一个共点的直线系,我们可以给出
为参数的直线系方程.要证明这个直线系的直线都过一定点,就是证明它是一个共点的直线系,我们可以给出![]() 的两个特殊值,得到直线系中的两条直线,它们的交点即是直线系中任何直线都过的定点.
的两个特殊值,得到直线系中的两条直线,它们的交点即是直线系中任何直线都过的定点.
另一思路是由于方程对任意的![]() 都成立,那么就以
都成立,那么就以![]() 为未知数,整理为关于
为未知数,整理为关于![]() 的一元一次方程,再由一元一次方程有无数个解的条件求得定点的坐标.
的一元一次方程,再由一元一次方程有无数个解的条件求得定点的坐标.
解法一:对于方程![]() ,令
,令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() .
.
解方程组![]() 得两直线的交点为
得两直线的交点为![]() .
.
将点![]() 代入已知直线方程左边,得:
代入已知直线方程左边,得:
![]()
![]() .
.
这表明不论![]() 为什么实数,所给直线均经过定点
为什么实数,所给直线均经过定点![]() .
.
解法二:将已知方程以![]() 为未知数,整理为:
为未知数,整理为:
![]() .
.
由于![]() 取值的任意性,有
取值的任意性,有
![]() ,解得
,解得![]() ,
,![]() .
.
所以所给的直线不论![]() 取什么实数,都经过一个定点
取什么实数,都经过一个定点![]() .
.
说明:(1)曲线过定点,即与参数无关,则参数的同次幂的系数为0,从而求出定点.
(2)分别令参数为两个特殊值,得方程组求出点的坐标,代入原方程满足,则此点为定点.
典型例题十二
例12 一年级为配合素质教育,利用一间教室作为学生绘画成果展览室.为节约经费,他们利用课桌作为展台,将装画的镜框旋置桌上,斜靠展出.已知镜框对桌面的倾角为![]() (
(![]() )镜框中,画的上、下边缘与镜框下边缘分别相距
)镜框中,画的上、下边缘与镜框下边缘分别相距![]()
![]() 、
、![]()
![]() (
(![]() ),学生距离镜框下缘多远看画的效果最佳?
),学生距离镜框下缘多远看画的效果最佳?
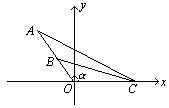
分析:建立如图所示的直角坐标系,![]() 为镜框边,
为镜框边,![]() 为画的宽度,
为画的宽度,![]() 为下边缘上的一点,则可将问题转化为:
为下边缘上的一点,则可将问题转化为:
已知![]() ,
,![]() ,
,![]() ,在
,在![]() 轴的正方向向上求一点
轴的正方向向上求一点![]() ,使
,使![]() 取最大值.
取最大值.
因为视角最大时,从理论上讲,看画的效果最佳(不考虑其他因素).
解:设![]() 点坐标为
点坐标为![]() (
(![]() ),从三角函数定义知
),从三角函数定义知![]() 、
、![]() 两点坐标分别为
两点坐标分别为![]() 、
、![]() ,于是直线
,于是直线![]() 、
、![]() 的斜率分别为
的斜率分别为
![]() ,
,![]() .
.
于是![]() ,
,
即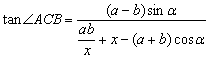 .
.
由于![]() 是锐角,且在
是锐角,且在![]() 上,则:
上,则:![]() ,
,
当且仅当![]() ,即
,即![]() 时,等号成立,此时
时,等号成立,此时![]() 取最大值,对应的点为
取最大值,对应的点为![]() ,因此,学生距离镜框下缘
,因此,学生距离镜框下缘![]() 处时,视角最大,即看画效果最佳.
处时,视角最大,即看画效果最佳.
说明:解决本题有两点至关重要:一是建立恰当的坐标系,使问题转化成解析几何问题求解;二是把问题进一步转化成求![]() 的最大值.如果坐标系选择不当,或选择求
的最大值.如果坐标系选择不当,或选择求![]() 的最大值,都将使问题变得复杂起来.
的最大值,都将使问题变得复杂起来.
本题是一个非常实际的数学应用问题,它不仅考查了直线的有关概念以及三角知识的结合运用,而且更重要的是考查了把实际问题转化为数学问题的能力.
典型例题十三
例13 知实数![]() ,
,![]() 满足
满足![]() ,求
,求![]() 的最小值.
的最小值.
分析:本题可使用减少变量法和数形结合法两种方法:![]() 可看成点
可看成点![]() 与
与![]() 之间的距离.
之间的距离.
解:(法1)由![]() 得
得![]() (
(![]() ),
),
则![]()
![]()
![]()
![]() ,
,
∴![]() 的最小值是2.
的最小值是2.
(法2)∵实数![]() ,
,![]() 满足
满足![]() ,
,
∴点![]() 在直线
在直线![]() 上.
上.
而![]() 可看成点
可看成点![]() 与点
与点![]() 之间的距离(如图所示)
之间的距离(如图所示)
显然![]() 的最小值就是点
的最小值就是点![]() 到直线
到直线![]() 的距离:
的距离:
![]() ,
,
∴![]() 的最小值为2.
的最小值为2.
说明:利用几何意义,可以使复杂问题简单化.形如![]() 的式子即可看成是两点间的距离,从而结合图形解决.
的式子即可看成是两点间的距离,从而结合图形解决.
典型例题十四
例14直线![]() 是
是![]() 中
中![]() 的平分线所在的直线,且
的平分线所在的直线,且![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,求顶点
,求顶点![]() 的坐标并判断
的坐标并判断![]() 的形状.
的形状.
分析:“角平分线”就意味着角相等,故可考虑使用直线的“到角”公式将“角相等”列成一个表达式.
解:(法1)由题意画出草图(如图所示).
∵点![]() 在直线
在直线![]() 上,∴设
上,∴设![]() ,
,
则![]() ,
,![]() ,
,![]() .
.
由图易知![]() 到
到![]() 的角等于
的角等于![]() 到
到![]() 的角,因此这两个角的正切也相等.
的角,因此这两个角的正切也相等.
∴![]() ,
,
∴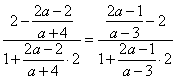 .
.
解得![]() .
.
∴![]() 的坐标为
的坐标为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() 是直角三角形.
是直角三角形.
(法2)设点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,则
,则![]() 必在直线
必在直线![]() 上.以下先求
上.以下先求![]() .
.
由对称性可得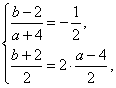
解得![]() ,∴
,∴![]() .
.
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.
由![]() 得
得![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
∴![]() 是直角三角形.
是直角三角形.
说明:(1)在解法1中设点![]() 坐标时,由于
坐标时,由于![]() 在直线
在直线![]() 上,故可设
上,故可设![]() ,而不设
,而不设![]() ,这样可减少未知数的个数.(2)注意解法2中求点
,这样可减少未知数的个数.(2)注意解法2中求点![]() 关于
关于![]() 的对称点
的对称点![]() 的求法:原理是线段
的求法:原理是线段![]() 被直线
被直线![]() 垂直平分.
垂直平分.
典型例题十五
例15 两条直线![]() ,
,![]() ,求分别满足下列条件的
,求分别满足下列条件的![]() 的值.
的值.
(1) ![]() 与
与![]() 相交;
(2)
相交;
(2) ![]() 与
与![]() 平行;
(3)
平行;
(3) ![]() 与
与![]() 重合;
重合;
(4) ![]() 与
与![]() 垂直;
(5)
垂直;
(5) ![]() 与
与![]() 夹角为
夹角为![]() .
.
分析:可先从平行的条件![]() (化为
(化为![]() )着手.
)着手.
解:由![]() 得
得![]() ,解得
,解得![]() ,
,![]() .
.
由![]() 得
得![]() .
.
(1)当![]() 且
且![]() 时,
时,![]() ,
,![]() 与
与![]() 相交;
相交;
(2)当![]() 时,
时,![]() .
.![]() ;
;
(3)当![]() 时,
时,![]() ,
,![]() 与
与![]() 重合;
重合;
(4)当![]() ,即
,即![]() ,
,![]() 时,
时,![]() ;
;
(5) ![]() ,
,![]() .
.
由条件有![]() .
.
将![]() ,
,![]() 代入上式并化简得
代入上式并化简得![]() ,
,![]() ;
;
![]() ,
,![]() .
.
∴当![]() 或-5或3时
或-5或3时![]() 与
与![]() 夹角为
夹角为![]() .
.
说明:由![]() 解得
解得![]() 或
或![]() ,此时两直线可能平行也可能重合,可将
,此时两直线可能平行也可能重合,可将![]() 的值代入原方程中验证是平行还是重合.当
的值代入原方程中验证是平行还是重合.当![]() 时两直线一定相交,此时应是
时两直线一定相交,此时应是![]() 且
且![]() .
.
典型例题十六
例16点![]() ,
,![]() 和
和![]() ,求过点
,求过点![]() 且与点
且与点![]() ,
,![]() 距离相等的直线方程.
距离相等的直线方程.
分析:可以用待定系数法先设出直线方程,再求之;也可从几何意义上考察这样的直线具有的特征.
解:(法1)设所求直线方程为![]() ,即
,即![]() ,由点
,由点![]() 、
、![]() 到直线的距离相等得:
到直线的距离相等得:
![]() .
.
化简得![]() ,则有:
,则有:![]() 或
或![]() ,
,
即![]() 或方程无解.
或方程无解.
方程无解表明这样的![]() 不存在,但过点
不存在,但过点![]() ,所以直线方程为
,所以直线方程为![]() ,它与
,它与![]() ,
,![]() 的距离都是3.
的距离都是3.
∴所求直线方程为![]() 或
或![]() .
.
(法2)设所求直线为![]() ,由于
,由于![]() 过点
过点![]() 且与
且与![]() ,
,![]() 距离相等,所以
距离相等,所以![]() 有两种情况,如下图:
有两种情况,如下图:
(1)当![]() ,
,![]() 在
在![]() 同侧时,有
同侧时,有![]() ,此时可求得
,此时可求得![]() 的方程为
的方程为![]() ,即
,即![]() ;
;
(2)当![]() ,
,![]() 在
在![]() 异侧时,
异侧时,![]() 必过
必过![]() 中点
中点![]() ,此时
,此时![]() 的方程为
的方程为![]() .
.
∴所求直线的方程为![]() 或
或![]() .
.
说明:该题如果用待定系数法解易漏掉![]() ,即斜率不存在的情况.所以无论解什么题目,只要图形容易画出,就应结合图形,用代数法、几何法配合来解.
,即斜率不存在的情况.所以无论解什么题目,只要图形容易画出,就应结合图形,用代数法、几何法配合来解.
典型例题十七
例17 经过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 的方程.
的方程.
分析:已知直线![]() 与直线
与直线![]() 平行,故
平行,故![]() 的斜率可求,又
的斜率可求,又![]() 过已知点
过已知点![]() ,利用点斜式可得到
,利用点斜式可得到![]() 的方程.另外由于
的方程.另外由于![]() 与已知直线平行,利用平行直线系方程,再由已知点
与已知直线平行,利用平行直线系方程,再由已知点![]() ,也可确定
,也可确定![]() 的方程.
的方程.
解法一:由已知直线![]() ,知其斜率
,知其斜率![]() .
.
又由![]() 与直线
与直线![]() 平行,所以直线
平行,所以直线![]() 的斜率
的斜率![]() .
.
又由直线![]() 经过已知点
经过已知点![]() ,所以利用点斜式得到直线
,所以利用点斜式得到直线![]() 的方程为:
的方程为:
![]() ,即
,即![]() .
.
解法二:因为直线![]() 平行于直线
平行于直线![]() ,所以可设直线
,所以可设直线![]() 的方程为
的方程为![]() .
.
又点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,解得
,解得![]() .
.
故直线![]() 的方程为
的方程为![]() .
.
说明:解法二使用的是平行直线系,并用了待定系数法来解.
典型例题十八
例18 过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 的方程.
的方程.
分析:已知直线![]() 与直线
与直线![]() 垂直,故
垂直,故![]() 的斜率可求,又
的斜率可求,又![]() 过已知点
过已知点![]() ,利用点斜式可得到
,利用点斜式可得到![]() 的方程.另外由于
的方程.另外由于![]() 与已知直线垂直,利用垂直直线系方程,再由已知点
与已知直线垂直,利用垂直直线系方程,再由已知点![]() ,也可确定
,也可确定![]() 的方程.
的方程.
解法一:由直线![]() ,知其斜率
,知其斜率![]() .
.
又由![]() 与直线
与直线![]() 垂直,所以直线
垂直,所以直线![]() 的斜率
的斜率![]() .
.
又因![]() 过已知点
过已知点![]() ,利用点斜式得到直线
,利用点斜式得到直线![]() 的方程为
的方程为
![]() ,即
,即![]() .
.
解法二:由直线![]() 与直线
与直线![]() 垂直,可设直线
垂直,可设直线![]() 的方程为:
的方程为:
![]() .
.
又由直线![]() 经过已知点
经过已知点![]() ,有
,有![]() .
.
解得![]() .因此直线
.因此直线![]() 的方程为
的方程为![]() .
.
说明:此题的解二中使用垂直直线系方程,并使用了待定系数法.
典型例题十九
例19知直线![]() 经过两条直线
经过两条直线![]() 与
与![]() 的交点,且与直线
的交点,且与直线![]() 的夹角为
的夹角为![]() ,求直线
,求直线![]() 的方程.
的方程.
分析:先求![]() 与
与![]() 的交点,再列两条直线夹角公式,利用
的交点,再列两条直线夹角公式,利用![]() 与
与![]() 夹角为
夹角为![]() ,求得
,求得![]() 的斜率.也可使用过两直线交点的直线系方程的方法省去求交点的过程,直接利用夹角公式求解.
的斜率.也可使用过两直线交点的直线系方程的方法省去求交点的过程,直接利用夹角公式求解.
解法一:由方程组![]() 解得直线
解得直线![]() 与
与![]() 的交点
的交点![]() .
.
于是,所求直线![]() 的方程为
的方程为![]() .
.
又由已知直线![]() 的斜率
的斜率![]() ,而且
,而且![]() 与
与![]() 的夹角为
的夹角为![]() ,故由两直线夹角正切公式,得
,故由两直线夹角正切公式,得
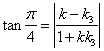 ,即
,即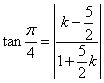 .
.
有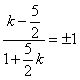 ,
,![]() ,
,
当![]() 时,解得
时,解得![]() ;当
;当![]() 时,解得
时,解得![]() .
.
故所求的直线![]() 的方程为
的方程为![]() 或
或![]() ,
,
即![]() 或
或![]() .
.
解法二:由已知直线![]() 经过两条直线
经过两条直线![]() 与
与![]() 的交点,则可设直线
的交点,则可设直线![]() 的方程为
的方程为
![]() , (*)
, (*)
即![]() .
.
又由![]() 与
与![]() 的夹角为
的夹角为![]() ,
,![]() 的方程为
的方程为![]() ,有
,有
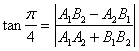 ,
,
即![]() ,也即
,也即![]() ,
,
从而![]() ,
,![]() .
.
解得![]() ,
,![]() .代入(*)式,可得直线
.代入(*)式,可得直线![]() 的方程为
的方程为
![]() 或
或![]() .
.
说明:此题用到两直线的夹角公式,注意夹角公式与到角公式的区别。解法二还用到了过两相交直线的交点的直线系方程,用它可以省去求交点的过程,但不一定这样的运算就简单,还要根据具体题目选择合适的方法。
典型例题二十
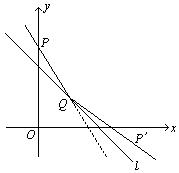
例20 直线![]() ,一束光线过点
,一束光线过点![]() ,以
,以![]() 的倾斜角投射到
的倾斜角投射到![]() 上,经
上,经![]() 反射,求反射线所在直线的方程.
反射,求反射线所在直线的方程.
分析:此题解法很多.如图,入射线与![]() 交于
交于![]() 点,则
点,则![]() 点的坐标易得.求反射线的方程只缺少一个条件,寻求这个条件的主要思路有:
点的坐标易得.求反射线的方程只缺少一个条件,寻求这个条件的主要思路有:
思路一:已知![]() 的倾斜角为
的倾斜角为![]() ,入射线的倾斜解为
,入射线的倾斜解为![]() ,可由三角形外角定理得到反射线的倾斜角.
,可由三角形外角定理得到反射线的倾斜角.
思路二:如图,由光线的反射定律可知,![]() 到
到![]() 的角等于
的角等于![]() 到反射线的角,可得到反射线的斜率.
到反射线的角,可得到反射线的斜率.
思路三:由光的反射性质,可知反射线所在直线除经过![]() 点外,还经过
点外,还经过![]() 点关于
点关于![]() 的对称点
的对称点![]() ,求得
,求得![]() 的坐标,反射线方程也可求得.
的坐标,反射线方程也可求得.
思路四:由直线![]() 为入射线和反射线所在直线交角的平分线,
为入射线和反射线所在直线交角的平分线,![]() 上任意一点到入射线和反射线的距离相等,也可求得反射线的斜率.
上任意一点到入射线和反射线的距离相等,也可求得反射线的斜率.
思路五:可求得![]() ,直线
,直线![]() 为
为![]() ,入射线和反射线关于
,入射线和反射线关于![]() 对称,利用反函数性质,由入射线的方程可以求出反射线的方程.
对称,利用反函数性质,由入射线的方程可以求出反射线的方程.
解法一:由已知入射线的倾斜角为![]() ,其斜率为
,其斜率为![]() ,又入射线过点
,又入射线过点![]() ,所以入射线所在直线的方程为:
,所以入射线所在直线的方程为:![]() .
.
解方程组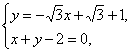 得交点
得交点![]() .
.
又因![]() 的倾斜角为
的倾斜角为![]() ,入射线
,入射线![]() 的倾斜角
的倾斜角![]() ,所以入射线与
,所以入射线与![]() 的夹角为
的夹角为![]() .
.
于是据外角定理![]() ,即反射线所在直线的斜率为
,即反射线所在直线的斜率为![]() .故反射线所在直线的方程为
.故反射线所在直线的方程为![]() ,即:
,即:
![]() .
.
解法二:由已知可得![]() ,
,![]() ,设反射线的斜率为
,设反射线的斜率为![]() ,则由入射线到
,则由入射线到![]() 的角等于
的角等于![]() 到反射线的角,可得
到反射线的角,可得
![]() ,即
,即![]() .
.
解得![]() .
.
以下求出![]() 点坐标,再由点斜式得反射线所在直线的方程(略).
点坐标,再由点斜式得反射线所在直线的方程(略).
解法三:由已知得入射线所在直线方程为![]() ,再与直线
,再与直线![]() 的方程联立得交点
的方程联立得交点![]() .
.
利用关于直线对称点的知识,求得点![]() 关于
关于![]() 的对称点
的对称点![]() .
.
又由反射线所在直线过![]() 与
与![]() 两点,它的方程为
两点,它的方程为![]() ,即:
,即:
![]() .
.
解法四:可求得入射线所在直线方程为![]() ,即
,即![]() ,入射线与
,入射线与![]() 交点为
交点为![]() .
.
于是可设反射线所在直线的方程为:![]() ,即
,即![]() .
.
由于直线![]() 为入射线与反射线夹角的平分线,则
为入射线与反射线夹角的平分线,则![]() 上的任一点到它们的距离相等,于是在
上的任一点到它们的距离相等,于是在![]() 上取点
上取点![]() ,有:
,有:
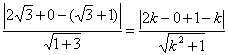 .
.
所以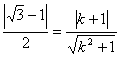 ,即
,即![]() .
.
故![]() ,
,![]() (等于入射线斜率,舍去).
(等于入射线斜率,舍去).
于是反射线的方程为:![]() ,即
,即![]() .
.
解法五:由点![]() ,得直线
,得直线![]() 的方程为
的方程为![]() .
.
又因入射线与反射线所在直线关于![]() 对称,点
对称,点![]() 关于直线
关于直线![]() 对称的点
对称的点![]() 的坐标为
的坐标为![]() .
.
由于反射线所在直线经过![]() 与
与![]() 两点,所以它的方程为:
两点,所以它的方程为:
![]() ,即
,即![]() .
.
典型例题二十一
例21 已知直线![]() ,试求:
,试求:
(1)点![]() 关于直线
关于直线![]() 的对称点坐标;
的对称点坐标;
(2)直线![]() 关于直线
关于直线![]() 对称的直线
对称的直线![]() 的方程;
的方程;
(3)直线![]() 关于点
关于点![]() 的对称直线方程.
的对称直线方程.
分析:对称问题可分为四种类型:①点关于点的对称点;②点关于直线的对称点;③直线关于直线的对称直线;④直线关于点的对称直线.对于①利用中点坐标公式即可.对于②需利用“垂直”“平分”两个条件.若③④在对称中心(轴),及一个曲线方程已知的条件下给出,则通常采取坐标转移法,其次对于对称轴(中心)是特殊直线,如:坐标轴、直线![]() ,采取特殊代换法,应熟练掌握.
,采取特殊代换法,应熟练掌握.
解:(1)设点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,
,
则线段![]() 的中点
的中点![]() 在对称轴
在对称轴![]() 上,且
上,且![]() .
.
∴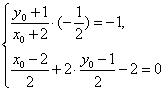
解之得: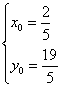
即![]() 坐标为
坐标为![]() .
.
(2)直线![]() 关于直线
关于直线![]() 对称的直线为
对称的直线为![]() ,则
,则![]() 上任一点
上任一点![]() 关于
关于![]() 的对称点
的对称点![]() 一定在直线
一定在直线![]() 上,反之也成立.
上,反之也成立.
由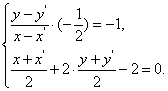
得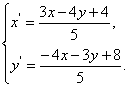
把![]() 代入方程
代入方程![]() 并整理,得:
并整理,得:![]()
即直线![]() 的方程为
的方程为![]() .
.
(3)设直线![]() 关于点
关于点![]() 的对称直线为
的对称直线为![]() ,则直线
,则直线![]() 上任一点
上任一点![]() 关于点
关于点![]() 的对称点
的对称点![]() 一定在直线
一定在直线![]() 上,反之也成立.
上,反之也成立.
由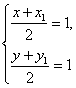 得
得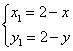
将![]() 代入直线
代入直线![]() 的方程得:
的方程得:![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
说明:本题是求有关对称点、对称直线的问题,主要用到中点坐标公式和直线垂直的斜率关系.
典型例题二十二
例22 已知直线![]() 和两点
和两点![]() 、
、![]() .
.
(1)在![]() 上求一点
上求一点![]() ,使
,使![]() 最小;
最小;
(2)在![]() 上求一点
上求一点![]() ,使
,使![]() 最大.
最大.
分析:较直接的思路是:用两点间的距离公式求出![]() 的表达式,再求它的最小值.这样计算量太大也不可行.我们可以求出
的表达式,再求它的最小值.这样计算量太大也不可行.我们可以求出![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,从而将
,从而将![]() 转化为
转化为![]() ,从而当
,从而当![]() 、
、![]() 、
、![]() 三点共线时,
三点共线时,![]() 才最小,对于
才最小,对于![]() 最大也可以利用这样的方法.
最大也可以利用这样的方法.
解:(1)如图,设![]() 关于
关于![]() 的对称点为
的对称点为![]()
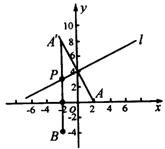
则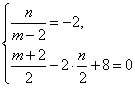
∴![]() ,
,![]() .
.
∴![]()
∴![]() 的的是
的的是![]() ,
,![]() 与
与![]() 的交点是
的交点是![]() ,
,
故所求的点为![]() .
.
(2)如下图,
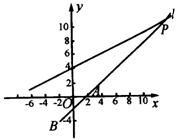
![]() 是方程
是方程![]() ,
,
即![]() .
.
代入![]() 的方程,得直线
的方程,得直线![]() 与
与![]() 的交点
的交点![]() ,
,
故所求的点![]() 为
为![]() .
.
说明:本例利用求对称点的方法巧妙地求出了所求点![]() 的坐标.
的坐标.
典型例题二十四
例24 已知点![]() ,
,![]() 和直线
和直线![]() ,求一点
,求一点![]() 使
使![]() ,且点
,且点![]() 到
到![]() 的距离等于2.
的距离等于2.
分析:为使![]() (如图),点
(如图),点![]() 必在线段
必在线段![]() 的垂直平分线上,又点
的垂直平分线上,又点![]() 到直线
到直线![]() 的距离为2,所以点
的距离为2,所以点![]() 又在距离
又在距离![]() 为2的平行于
为2的平行于![]() 的直线上,求这两条直线的交点即得所求点
的直线上,求这两条直线的交点即得所求点![]() .
.
解:设点![]() 的坐标为
的坐标为![]() .
.
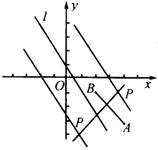
∵![]() ,
,![]() .
.
∴![]() 的中点
的中点![]() 的坐标为
的坐标为![]() .
.
又![]() 的斜率
的斜率![]() .
.
∴![]() 的垂直平分线方程为
的垂直平分线方程为![]() ,即
,即![]() .
.
而![]() 在直线
在直线![]() 上.
上.
∴![]() . ①
. ①
又已知点![]() 到
到![]() 的距离为2.
的距离为2.
∴点![]() 必在于
必在于![]() 平行且距离为2的直线上,
平行且距离为2的直线上,
设直线方程为![]() ,
,
由两条平行直线之间的距离公式得:
![]()
∴![]() 或
或![]() .
.
∴点![]() 在直线
在直线![]() 或
或![]() 上.
上.
∴![]() 或
或![]() ②
②
由∴①②得:![]() ,
,![]() 或
或![]() ,
,![]() .
.
∴点![]() 或
或![]() 为所求的点.
为所求的点.
说明:在平面几何中,常用交轨法作图得点![]() 的位置,而在解析几何中,则是将直线用方程来表示,用求方程组的解的方式来求得点
的位置,而在解析几何中,则是将直线用方程来表示,用求方程组的解的方式来求得点![]() 的坐标.这是解析法的重要应用,也是其方便之处.
的坐标.这是解析法的重要应用,也是其方便之处.