典型例题一
例1
在二项式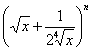 的展开式中,前三项的系数成等差数列,求展开式中所有有理项.
的展开式中,前三项的系数成等差数列,求展开式中所有有理项.
分析:本题是典型的特定项问题,涉及到前三项的系数及有理项,可以通过抓通项公式解决.
解:二项式的展开式的通项公式为:
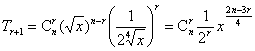
前三项的![]()
得系数为:![]() ,
,
由已知:![]() ,
,
∴![]()
通项公式为
![]() 为有理项,故
为有理项,故![]() 是4的倍数,
是4的倍数,
∴![]()
依次得到有理项为![]() .
.
说明:本题通过抓特定项满足的条件,利用通项公式求出了r的取值,得到了有理项.类似地,![]() 的展开式中有多少项是有理项?可以通过抓通项中r的取值,得到共有17项.
的展开式中有多少项是有理项?可以通过抓通项中r的取值,得到共有17项.
典型例题二
例2
求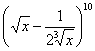 的展开式中,系数绝对值最大的项以及系数最大的项.
的展开式中,系数绝对值最大的项以及系数最大的项.
分析:本题仍然属于抓通项公式解决特定项的问题,但是系数的绝对值的最大值或系数的最大值,需要对所有项的系数的变化规律进行研究.由于系数的绝对值都是正数,我们可以用作商来研究系数绝对值的变化情况,另外各项系数正负交替,又便于用系数绝对值的大小变化抓系数的最大值.
解:展开式的通项公式为:![]()
系数的绝对值为![]() ,记为
,记为![]() .
.
用前后两项系数的绝对值作商得:
![]()
令![]() 得:
得:![]() 即
即![]() 、1、2时,上述不等式成立.
、1、2时,上述不等式成立.
所以,系数的绝对值从第1项到第4项增加,以后逐项减小.
系数绝对值最大的项为第4项,![]() .
.
从系数绝对值的变化情况及系数的正负交替,只要比较第3项与第5项的系数,
![]()
所以,系数最大的项为第5项,![]() .
.
典型例题三
例3
已知![]() ,求:(1)
,求:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
分析:本题是有关展开式系数和的问题,通过对等式中字母的赋值,往往会得到此类问题的结果.字母经常取的值有0、1、-1等.
解:(1)取![]() 可得
可得![]() ,
,
取![]() 得
得![]() .
.
∴![]() .
.
(2)取![]() 得
得![]() ,
,
记![]() .
.
∴![]() .
.
可得![]()
从而![]() .
.
(3)从(2)的计算已知![]() .
.
说明:赋值法不仅可以用来求二项展开式的系数和,对于展开式为多项式的代数式的系数和大多数也能用此方法解决,如:![]() 的展开式中各项的系数和为多少?可以看到
的展开式中各项的系数和为多少?可以看到![]() 的展开式仍是多项式,令
的展开式仍是多项式,令![]() ,即得各项系数和为
,即得各项系数和为![]() .再比如:
.再比如:![]() ,则
,则![]() 等于多少?本题可以由取
等于多少?本题可以由取![]() 得到各项系数和,取
得到各项系数和,取![]() 得到奇数项系数和减去偶数项系数和,两式相加可得
得到奇数项系数和减去偶数项系数和,两式相加可得![]() .此外,为了赋值的需要,有时需要用一个新的二项式替换原来二项式,只要它们的系数等同即可.如:
.此外,为了赋值的需要,有时需要用一个新的二项式替换原来二项式,只要它们的系数等同即可.如:![]() 的展开式中各项的系数和是多少?我们可以用一个更简单的二项式
的展开式中各项的系数和是多少?我们可以用一个更简单的二项式![]() 代替原来的二项式,它们的系数并不改变,令
代替原来的二项式,它们的系数并不改变,令![]() 便得各项系数和为
便得各项系数和为![]() .
.
典型例题四
例4
(1)求![]() 展开式中
展开式中![]() 的系数;(2)求
的系数;(2)求![]() 展开式中的常数项.
展开式中的常数项.
分析:本题的两小题都不是二项式展开,但可以转化为二项式展开的问题,(1)可以视为两个二项展开式相乘;(2)可以经过代数式变形转化为二项式.
解:(1)![]() 展开式中的
展开式中的![]() 可以看成下列几种方式得到,然后合并同类项:
可以看成下列几种方式得到,然后合并同类项:
用![]() 展开式中的常数项乘以
展开式中的常数项乘以![]() 展开式中的
展开式中的![]() 项,可以得到
项,可以得到![]() ;用
;用![]() 展开式中的一次项乘以
展开式中的一次项乘以![]() 展开式中的
展开式中的![]() 项可得到
项可得到![]() ;用
;用![]() 中的
中的![]() 乘以
乘以![]() 展开式中的
展开式中的![]() 可得到
可得到![]() ;用
;用 ![]() 中的
中的![]() 项乘以
项乘以![]() 展开式中的
展开式中的![]() 项可得到
项可得到![]() ,合并同类项得
,合并同类项得![]() 项为:
项为:
![]() .
.
(2)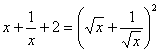
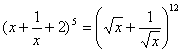 .
.
由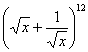 展开式的通项公式
展开式的通项公式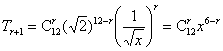 ,可得展开式的常数项为
,可得展开式的常数项为![]() .
.
说明:问题(2)中将非二项式通过因式分解转化为二项式解决.这时我们还可以通过合并项转化为二项式展开的问题来解决.
典型例题五
例5
求![]() 展开式中
展开式中![]() 的系数.
的系数.
分析:![]() 不是二项式,我们可以通过
不是二项式,我们可以通过![]() 或
或![]() 把它看成二项式展开.
把它看成二项式展开.
解:方法一:![]()
![]()
其中含![]() 的项为
的项为![]() .
.
含![]() 项的系数为6.
项的系数为6.
方法二:![]()
![]()
其中含![]() 的项为
的项为![]() .
.
∴![]() 项的系数为6.
项的系数为6.
方法3:本题还可通过把![]() 看成6个
看成6个![]() 相乘,每个因式各取一项相乘可得到乘积的一项,
相乘,每个因式各取一项相乘可得到乘积的一项,![]() 项可由下列几种可能得到.5个因式中取x,一个取1得到
项可由下列几种可能得到.5个因式中取x,一个取1得到![]() .
.
3个因式中取x,一个取![]() ,两个取1得到
,两个取1得到![]() .
.
1个因式中取x,两个取![]() ,三个取1得到
,三个取1得到![]() .
.
合并同类项为![]() ,
,![]() 项的系数为6.
项的系数为6.
典型例题六
例6
求证:(1)![]() ;
;
(2)![]() .
.
分析:二项式系数的性质实际上是组合数的性质,我们可以用二项式系数的性质来证明一些组合数的等式或者求一些组合数式子的值.解决这两个小题的关键是通过组合数公式将等式左边各项变化的等数固定下来,从而使用二项式系数性质![]() .
.
解:(1)![]()
∴左边![]()
![]() 右边.
右边.
(2)![]()
![]() .
.
∴左边![]()
![]() 右边.
右边.
说明:本题的两个小题都是通过变换转化成二项式系数之和,再用二项式系数的性质求解.此外,有些组合数的式子可以直接作为某个二项式的展开式,但这需要逆用二项式定理才能完成,所以需仔细观察,我们可以看下面的例子:求![]() 的结果.仔细观察可以发现该组合数的式与
的结果.仔细观察可以发现该组合数的式与![]() 的展开式接近,但要注意:
的展开式接近,但要注意:
![]()
![]()
![]()
从而可以得到:![]() .
.
典型例题七
例7
利用二项式定理证明:![]() 是64的倍数.
是64的倍数.
分析:64是8的平方,问题相当于证明![]() 是
是![]() 的倍数,为了使问题向二项式定理贴近,变形
的倍数,为了使问题向二项式定理贴近,变形![]() ,将其展开后各项含有
,将其展开后各项含有![]() ,与
,与![]() 的倍数联系起来.
的倍数联系起来.
解:∵![]()
![]()
![]()
![]()
![]()
![]() 是64的倍数.
是64的倍数.
说明:利用本题的方法和技巧不仅可以用来证明整除问题,而且可以用此方程求一些复杂的指数式除以一个数的余数.
典型例题八
例8 展开![]() .
.
分析1:用二项式定理展开式.
解法1:![]()
![]()
![]()
![]()
分析2:对较繁杂的式子,先化简再用二项式定理展开.
解法2:![]()
![]()
![]()
![]()
![]() .
.
说明:记准、记熟二项式![]() 的展开式,是解答好与二项式定理有关问题的前提条件.对较复杂的二项式,有时先化简再展开会更简便.
的展开式,是解答好与二项式定理有关问题的前提条件.对较复杂的二项式,有时先化简再展开会更简便.
典型例题九
例9 若将![]() 展开为多项式,经过合并同类项后它的项数为( ).
展开为多项式,经过合并同类项后它的项数为( ).
A.11 B.
分析:![]() 看作二项式
看作二项式![]() 展开.
展开.
解:我们把![]() 看成
看成![]() ,按二项式展开,共有
,按二项式展开,共有![]() “项”,即
“项”,即
![]() .
.
这时,由于“和”中各项![]() 的指数各不相同,因此再将各个二项式
的指数各不相同,因此再将各个二项式![]() 展开,
展开,
不同的乘积![]() (
(![]() )展开后,都不会出现同类项.
)展开后,都不会出现同类项.
下面,再分别考虑每一个乘积![]() (
(![]() ).
).
其中每一个乘积展开后的项数由![]() 决定,
决定,
而且各项中![]() 和
和![]() 的指数都不相同,也不会出现同类项.
的指数都不相同,也不会出现同类项.
故原式展开后的总项数为![]() ,
,
∴应选D.
典型例题十
例10 若![]() 的展开式的常数项为
的展开式的常数项为![]() ,求
,求![]() .
.
分析:题中![]() ,当
,当![]() 时,把三项式
时,把三项式![]() 转化为
转化为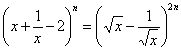 ;当
;当![]() 时,同理
时,同理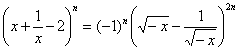 .然后写出通项,令含
.然后写出通项,令含![]() 的幂指数为零,进而解出
的幂指数为零,进而解出![]() .
.
解:当![]() 时
时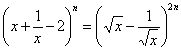 ,其通项为
,其通项为
![]() ,
,
令![]() ,得
,得![]() ,
,
∴展开式的常数项为![]() ;
;
当![]() 时,
时,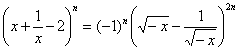 ,
,
同理可得,展开式的常数项为![]() .
.
无论哪一种情况,常数项均为![]() .
.
令![]() ,以
,以![]() ,逐个代入,得
,逐个代入,得![]() .
.
典型例题十一
例11 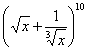 的展开式的第3项小于第4项,则
的展开式的第3项小于第4项,则![]() 的取值范围是______________.
的取值范围是______________.
分析:首先运用通项公式写出展开式的第3项和第4项,再根据题设列出不等式即可.
解:使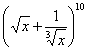 有意义,必须
有意义,必须![]() ;
;
依题意,有![]() ,即
,即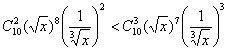 .
.
∴![]() (∵
(∵![]() ).
).
解得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.
∴应填:![]() .
.
典型例题十二
例12 已知![]() 的展开式中有连续三项的系数之比为
的展开式中有连续三项的系数之比为![]() ,这三项是第几项?若展开式的倒数第二项为
,这三项是第几项?若展开式的倒数第二项为![]() ,求
,求![]() 的值.
的值.
解:设连续三项是第![]() 、
、![]() 、
、![]() 项(
项(![]() 且
且![]() ),则有
),则有![]() ,
,
即![]() .
.
∴![]() .
.
∴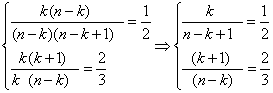
![]() ,
,![]() 所求连续三项为第
所求连续三项为第![]() 、
、![]() 、
、![]() 三项.
三项.
又由已知,![]() .即
.即![]() .
.
两边取以![]() 为底的对数,
为底的对数,![]() ,
,![]() ,
,
∴![]() ,或
,或![]() .
.
说明:当题目中已知二项展开式的某些项或某几项之间的关系时,常利用二项式通项,根据已知条件列出某些等式或不等式进行求解.
典型例题十三
例13 ![]() 的展开式中第
的展开式中第![]() 项与第
项与第![]() 项的系数相等,求展开式中二项式系数最大的项和系数最大的项.
项的系数相等,求展开式中二项式系数最大的项和系数最大的项.
分析:根据已知条件可求出![]() ,再根据
,再根据![]() 的奇偶性;确定二项式系数最大的项.
的奇偶性;确定二项式系数最大的项.
解:![]() ,
,![]() ,依题意有
,依题意有
![]() .
.
∴![]() 的展开式中,二项式系数最大的项为
的展开式中,二项式系数最大的项为![]() .
.
设第![]() 项系数最大,则有
项系数最大,则有
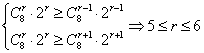 .
.
∴![]() 或
或![]() (∵
(∵![]() ).
).
∴系娄最大的项为:![]() ,
,![]() .
.
说明:(1)求二项式系数最大的项,根据二项式系数的性质,![]() 为奇数时中间两项的二项式系数最大,
为奇数时中间两项的二项式系数最大,![]() 为偶数时,中间一项的二项式系数最大.
为偶数时,中间一项的二项式系数最大.
(2)求展开式中系数最大项与求二项式系数最大项是不同的,需根据各项系数的正、负变化情况,一般采用列不等式,解不等式的方法求得.
典型例题十四
例14 设![]() (
(![]() ),若其展开式中关于
),若其展开式中关于![]() 的一次项的系数和为
的一次项的系数和为![]() ,问
,问![]() 为何值时,含
为何值时,含![]() 项的系数取最小值?并求这个最小值.
项的系数取最小值?并求这个最小值.
分析:根据已知条件得到![]() 的系数关于
的系数关于![]() 的二次表达式,然后利用二次函数性质探讨最小值问题.
的二次表达式,然后利用二次函数性质探讨最小值问题.
解:![]() .
.
![]()
![]() .
.
∵![]() ,
,
∴![]() 或
或![]() ,
,![]() 或
或![]() 时,
时,![]() 项系数最小,最小值为
项系数最小,最小值为![]() .
.
说明:二次函数![]() 的对称轴方程为
的对称轴方程为![]() ,即
,即![]() ,由于
,由于![]() 、
、![]() 距
距![]() 等距离,且对
等距离,且对![]() ,
,![]() 、
、![]() 距
距![]() 最近,所以
最近,所以![]() 的最小值在
的最小值在![]() 或
或![]() 处取得.
处取得.
典型例题十五
例15 若![]() ,
,
求(1) ![]() ;(2)
;(2) ![]() ;(3)
;(3) ![]() .
.
解:(1)令![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() . ①
. ①
∴![]() .
.
(2)令![]() ,则
,则![]() ②
②
由![]() 得:
得:![]()
(3)由![]() 得:
得:
![]()
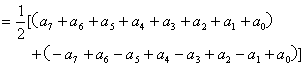
![]() .
.
说明:(1)本解法根据问题恒等式特点来用“特殊值”法.这是一种重要的方法,它适用于恒等式.
(2)一般地,对于多项式![]() ,
,![]() 的各项的系数和为
的各项的系数和为![]() :
:
![]() 的奇数项的系数和为
的奇数项的系数和为![]() .
.
![]() 的偶数项的系数和为
的偶数项的系数和为![]() .
.
典型例题十六
例16 填空:(1) ![]() 除以
除以![]() 的余数_____________;(2)
的余数_____________;(2) ![]() 除以
除以![]() 的余数是________________.
的余数是________________.
分析(1):将![]() 分解成含
分解成含![]() 的因数,然后用二项式定理展开,不含
的因数,然后用二项式定理展开,不含![]() 的项就是余数.
的项就是余数.
解:![]()
![]()
![]()
![]()
![]()
![]()
又∵余数不能为负数,需转化为正数
∴![]() 除以
除以![]() 的余数为
的余数为![]()
∴应填:![]()
分析(2):将![]() 写成
写成![]() ,然后利用二项式定理展开.
,然后利用二项式定理展开.
解:![]()
![]()
![]()
容易看出该式只有![]() 不能被
不能被![]() 整除,因此
整除,因此![]() 除以
除以![]() 的余数,即
的余数,即![]() 除以
除以![]() 的余数,故余数为
的余数,故余数为![]() .∴应填:
.∴应填:![]() .
.
典型例题十七
例17 求证:对于![]() ,
,![]() .
.
证明:![]() 展开式的通项
展开式的通项
![]()
![]()
![]() .
.
![]() 展开式的通项
展开式的通项
![]()
![]() .
.
由二项式展开式的通项明显看出![]() ,
,
所以![]() .
.
说明:本题的两个二项式中的两项为正项,且有一项相同,证明时,根据题设特点,采用比较通项大小的方法完成本题证明.
典型例题十八
例18 在![]() 的展开式中
的展开式中![]() 的系数为( ).
的系数为( ).
A.160 B.
分析:本题考查二项式定理的通项公式的运用.应想办法将三项式转化为二项式求解.
解法1:由![]() ,
,
得![]()
![]() .
.
再一次使用通项公式得,![]() ,
,
这里![]() ,
,![]() .
.
令![]() ,即
,即![]() .
.
所以![]() ,
,![]() ,由此得到
,由此得到![]() 的系数为
的系数为![]() .
.
解法2:由![]() ,知
,知![]() 的展开式中
的展开式中![]() 的系数为
的系数为![]() ,
,
常数项为![]() ,
,![]() 的展开式中
的展开式中![]() 的系数为
的系数为![]() ,常数项为
,常数项为![]() .
.
因此原式中![]() 的系数为
的系数为![]() .
.
解法3:将![]() 看作
看作![]() 个三项式相乘,
个三项式相乘,
展开式中![]() 的系数就是从其中一个三项式中取
的系数就是从其中一个三项式中取![]() 的系数
的系数![]() ,
,
从另外![]() 个三项式中取常数项相乘所得的积,即
个三项式中取常数项相乘所得的积,即![]() .
.
∴应选B.
典型例题十九
例19 已知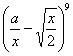 的展开式中
的展开式中![]() 的系数为
的系数为![]() ,常数
,常数![]() 的值为___________.
的值为___________.
分析:利用二项式的通项公式.
解:在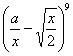 的展开式中,
的展开式中,
通项公式为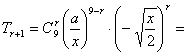
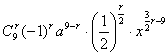 .
.
根据题设,![]() ,所以
,所以![]() .代入通项公式,得
.代入通项公式,得![]() .
.
根据题意,![]() ,所以
,所以![]() .
.
∴应填:![]() .
.
典型例题二十
例20 (1)求证:![]()
(2)若![]() ,求
,求![]() 的值.
的值.
分析:(1)注意观察![]() 的系数、指数特征,即可通过赋值法得到证明.(2)注意到
的系数、指数特征,即可通过赋值法得到证明.(2)注意到![]()
![]() ,再用赋值法求之.
,再用赋值法求之.
解:(1)在公式![]() 中令
中令![]() ,即有
,即有
![]()
![]()
∴等式得证.
(2)在展开式![]() 中,
中,
令![]() ,得
,得![]() ;
;
令![]() ,得
,得![]() .
.
∴原式![]()
![]() .
.
说明:注意“赋值法”在证明或求值中的应用.赋值法的模式是,在某二项展开式,如
![]() 或
或![]()
![]()
![]() 中,对任意的
中,对任意的![]() (
(![]() )该式恒成立,那么对
)该式恒成立,那么对![]() 中的特殊值,该工也一定成立.特殊值
中的特殊值,该工也一定成立.特殊值![]() 如何选取,没有一成不变的规律,需视具体情况而定,其灵活性较强.一般取
如何选取,没有一成不变的规律,需视具体情况而定,其灵活性较强.一般取![]() 较多.一般地,多项式
较多.一般地,多项式![]() 的各项系数和为
的各项系数和为![]() ,奇数项系数和为
,奇数项系数和为![]() ,偶次项系数和为
,偶次项系数和为![]() .二项式系数的性质
.二项式系数的性质![]() 及
及![]() 的证明就是赋值法应用的范例.
的证明就是赋值法应用的范例.
典型例题二十一
例21 若![]() ,求证明:
,求证明:![]() 能被
能被![]() 整除.
整除.
分析:考虑先将![]() 拆成与
拆成与![]() 的倍数有关的和式,再用二项式定理展开.
的倍数有关的和式,再用二项式定理展开.
解:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
∵![]() ,
,![]() ,
,![]() ,…均为自然数,
,…均为自然数,
∴上式各项均为![]() 的整数倍.
的整数倍.
∴原式能被![]() 整除.
整除.
说明:用二项式定理证明整除问题,大体上就是这一模式,先将某项凑成与除数有关的和式,再展开证之.该类题也可用数学归纳法证明,但不如用二项式定理证明简捷.
典型例题二十二
例22 已知![]() 的展开式各项系数和比它的二项式系数和大
的展开式各项系数和比它的二项式系数和大![]() .
.
(1)求展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
分析:先由条件列方程求出![]() .(1)需考虑二项式系数的性质;(2)需列不等式确定
.(1)需考虑二项式系数的性质;(2)需列不等式确定![]() .
.
解:令![]() 得展开式的各项系数之和为
得展开式的各项系数之和为![]() ,而展开式的二项式系数的和为
,而展开式的二项式系数的和为
![]() ,
,
∴有![]() .
.
∴![]() .
.
(1)∵![]() ,故展开式共有
,故展开式共有![]() ,其中二项式系数最大的项为第三、第四两项.
,其中二项式系数最大的项为第三、第四两项.
∴![]() ,
,
![]() .
.
(2)设展开式中第![]() 项的系数最大.
项的系数最大.
![]() ,
,
故有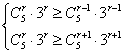
即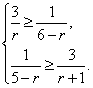
解得![]() .∵
.∵![]() ,
,
∴![]() ,即展开式中第
,即展开式中第![]() 项的系数最大.
项的系数最大.
![]()
说明:展开式中二项式系数最大的项与系数最大的项是两个不同的概念,因此其求法亦不同.前者用二项式系数的性质直接得出,后者要列不等式组;解不等式组时可能会求出几个![]() ,这时还必须算出相应项的系数后再比较大小.
,这时还必须算出相应项的系数后再比较大小.
典型例题二十三
例23 求证:(1) ![]() ;
;
(2) ![]() (
(![]() ,
,![]() )
)
分析:(1)注意到两列二项式两乘后系数的特征,可构造一个函数;也可用构造一个组合问题的两种不同解法找到思路.(2)同上构造函数,赋值.
证明:(1)(法1)∵![]() ,
,
∴![]() .
.
∴此式左右两边展开式中![]() 的系数必相等.
的系数必相等.
左边![]() 的系数是
的系数是![]() ,右边
,右边![]() 的系数是
的系数是
![]() ,
,
∴![]() .
.
等式成立.
(法2)设想有下面一个问题:要从![]() 个不同元素中取出
个不同元素中取出![]() 个元素,共有多少种取法?该问题可有两种解法.一种解法是明显的,即直接由组合数公式可得出结论:有
个元素,共有多少种取法?该问题可有两种解法.一种解法是明显的,即直接由组合数公式可得出结论:有![]() 种不同取法.第二种解法,可将
种不同取法.第二种解法,可将![]() 个元素分成两组,第一组有
个元素分成两组,第一组有![]() 个元素,第二组有
个元素,第二组有![]() 个元素,则从
个元素,则从![]() 个元素中取出
个元素中取出![]() 个元素,可看成由这两组元素中分别取出的元素组成,取法可分成
个元素,可看成由这两组元素中分别取出的元素组成,取法可分成![]() 类:从第一组取
类:从第一组取![]() 个,第二组不取,有
个,第二组不取,有![]() 种取法;从第一组取
种取法;从第一组取![]() 个,从第二组取
个,从第二组取![]() 个,有
个,有![]() 种取法,…,第一组不取,从第二组取
种取法,…,第一组不取,从第二组取![]() 个.因此取法总数是
个.因此取法总数是![]() .
.
而该问题的这两种解法答案应是一致的,故有
![]() .
.
(2)∵![]() 为偶数,
为偶数,
∴![]() ;
;
![]() .
.
两式相加得![]() ,
,
∴![]() .
.
说明:构造函数赋值法,构造问题双解法,拆项法、倒序相加法都是证明一些组合数恒等式(或求和)的常用方法.