高二文科数学下学期第一次月考试题
（考试时间：120分钟 总分：150分）
命题人：漳平一中 范思南 审题人：漳平一中 苏新妙
一、选择题（每小题5分，共60分）
1、已知集合
，
则
（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
2、设有一个回归方程为
变量
增加一个单位，则（ ）
Ａ、
平均增加3个单位 Ｂ、平均减少4个单位
Ｃ、平均减少3个单位 Ｄ、平均增加4个单位
3、下面四个平面图形中，顶点数Ｖ，边数Ｅ和区域数Ｆ的关系式是（ ）
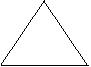
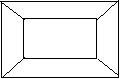
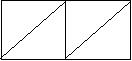
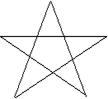
Ａ、Ｖ+Ｆ－Ｅ＝2 Ｂ、Ｖ+Ｆ－Ｅ＝1
Ｃ、Ｖ+Ｆ－Ｅ＝0 Ｄ、Ｖ+Ｆ－Ｅ＝3
4、如果方程
的两根为
那么
的值为（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、－6
5、二次函数
中，
则函数的零点个数是（ ）
Ａ、1个 Ｂ、2个 Ｃ、0个 Ｄ、无法确定
6、观察下图规律，在其最下面一行的空格内画上合适的图形是（ ）
| ☆ | ● | □ | ▲ |
| △ | ★ | ○ | ■ |
| ▲ | ☆ | ● | |
Ａ、△★○■ Ｂ、○■△★ Ｃ、○★△■ Ｄ、□●☆▲
7、设函数
，
则
（ ）
Ａ、3 Ｂ、－3 Ｃ、2 Ｄ、7
8、已知数列
前
项和
且
通过计算
，猜想
等于（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
9、已知复数
若
为实数 则
（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
10、下列哪个程序框图能实现交换
两个变量的值（ ）
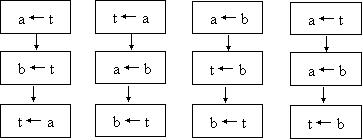
Ａ Ｂ Ｃ Ｄ
11、已知函数
若
，
则（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
与
的大小不能确定
12、函数
在
恒为正，则实数
的范围是（ ）
Ａ、
Ｂ、
Ｃ、
Ｄ、
二、填空题（每小题4分，共16分）
13、设集合
若
，则实数
的取值范围为 。
14、若集合
则
。
15、已知
，求取值范围为 。
16、已知
且
，函数
与
的图象有两个交点，则取值范围为
三、解答题（共74分）
17、（12分）已知复数
（1）求
（2）如果
求实数
18、（12分）已知函数
定义域为（－2,2），函数
（1）求函数
的定义域；
（2）若是奇函数且在定义域上单调递减，求不等式
的解集。
19、（12分）设甲、乙两人每次射击命中目标的概率分别为
和
，且各次射击相互独立。
（1）若甲、乙各射击一次，求甲命中但乙未命中目标的概率；
（2）若甲、乙各射击两次，求甲命中目标的次数大于乙命中目标次数的概率。
20、（12分）已知函数
（1）若函数的值域为
求的值；
（2）若函数的值都是非负数，求函数
的值域。
21、（12分）某服装厂生产一种服装，每件服装的成本为40元，出厂单价定为60元，为鼓励销售商订购，决定当一次订购量超过100件时，每多订购一件，订购的全部服装的出厂单价就降低0.02元，根据市场调查，销售商一次订购量不会超过500件。
（1）设一次订购量为件，服装的实际出厂单价为
元，写出函数
的表达式；
（2）当销售商一次订购450件服装时，该服装厂获得的利润是多少元？（服装厂售出一件服装的利润＝实际出厂价－成本）
22、（14分）已知
（1）求
的定义域；
（2）在函数的图象上是否存在不同的两点，使经过这两点的直线平行轴；
（3）当满足什么条件时，在区间
上恒取正值。
“华安、连城、永安、漳平一中，龙海二中” 五校联考
2007－2008学年下学期第一次月考
高二文科数学答题卷
| 题号 | 选择题 | 填空题 | 17 | 18 | 19 | 20 | 21 | 22 | 得分 |
| 得分 |
二、填空题：
13、 14、 15、 16、
| ||||
| ||||
|
|
|
|
“华安、连城、永安、漳平一中，龙海二中” 五校联考
2007－2008学年下学期第一次月考
高二文科数学参考答案
一、选择题（每小题5分，共60分）、
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | Ｄ | Ｂ | Ａ | Ｃ | Ｂ | Ｂ | Ｄ | Ｂ | Ｂ | Ｂ | Ａ | Ｃ |
二、填空题（每小题4分，共16分）
13、
14、
15、
16、
12、当 不成立
当
时 
有
恒成立
三、解答题（共74分）
17、解：（1）
…………………………………………4分
（2）
…………………8分
………………………………………………12分
18、解：（1）由题意可知
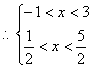……………………4分
得
故的定义域为
……………………………………………6分
（2）由
得
…………………………………………………………7分
是奇函数 
……………………………………8分
而在（－2,2）上单调递减
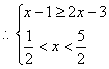………………………………………………………………10分
…………………………………………………………………………11分
解集为
…………………………………………………………12分
19、解：（1）Ａ表示甲命中目标，Ｂ表示乙命中目标
答：甲中乙未中目标概率为…………………………………………6分
（2）设
表示甲在两次射击中命中
次
表示乙在两次射击中命中次
答：甲命中目标次数大于乙命中目标次数概率为
。………………………12分
20、解（1）
函数值域为
△
…………………………………………………………2分
故
或
……………………………………………………………………4分
（2）对一切
函数值是非负数
△
…………………………………………………………6分
…………………………8分
在[
]上是减函数
……………………………………………10分
值域
……………………………………………………12分
21、解：（1）当
时 
当
时，
所以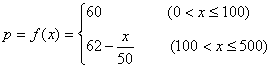
…………6分
（2）设销售商的一次购量为件时，工厂获得的利润为元
则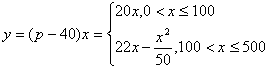
…………10分
当销售商一次订购450件服装时，该厂获得的利润是5850元……12分
22、解：（1）
得
函数定义域为
……………………………………4分
（2）设
则
即故在上是增函数
不存在不同的两点，使过这两点的直线平行轴………………………………10分
（3）在上是增函数
要设在上恒为正值
……………………………………………………………………………14分