高二文科(必修3)模块测试卷数学试题(文科)
(时间:120分钟 满分:150分)
说明:请将答案填写在答卷纸上,考试结束后只交答案卷。
一、选择题:(本题共12小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是正确的)
1.已知物体运动的方程是![]() (
(![]() 的单位:
的单位:![]() ;
; ![]() 的单位:
的单位:![]() ),则该物体在
),则该物体在![]()
![]() 时的速度为( )
时的速度为( )![]() 。 ( )
。 ( )
A. 0 B.
2.设k>1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是 ( )
A.长轴在y轴上的椭圆 B.长轴在x轴上的椭圆
C.实轴在y轴上的双曲线 D.实轴在x轴上的双曲线
3.已知椭圆![]() 的两准线间的距离为
的两准线间的距离为![]() ,离心率为
,离心率为![]() ,则椭圆方程为( )
,则椭圆方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.过点![]() 作直线
作直线![]() ,与抛物线
,与抛物线![]() 只有一个公共点,满足条件的直线有( )条
只有一个公共点,满足条件的直线有( )条
A.0条 B.1条 C.2条 D.条
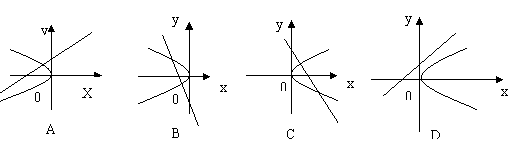 5.方程
5.方程![]() 的图像只可能是下图中 ( )
的图像只可能是下图中 ( )
6.函数![]() 在闭区间[-3,0]上的最大值、最小值分别是 ( )
在闭区间[-3,0]上的最大值、最小值分别是 ( )
A. 1,-17 B.3,
7.设![]() 是函数
是函数![]() 的导函数,
的导函数,
|
的图象最有可能的是 ( )
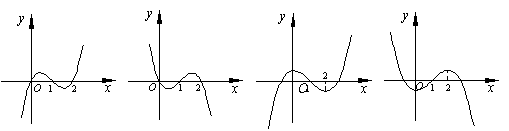 |
A. B. C. D.
8.等腰![]() 内接于抛物线
内接于抛物线![]() ,
,![]() 是抛物线的顶点,
是抛物线的顶点,![]() ,则
,则![]() 的面积是 ( )
的面积是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
9.有一条光线沿直线![]() 射到抛物线
射到抛物线![]() 上的一点
上的一点![]() ,经抛物线反射后,反射光线所在的直线与抛物线的另一个交点是
,经抛物线反射后,反射光线所在的直线与抛物线的另一个交点是![]() ,
,![]() 是抛物线的焦点,则弦
是抛物线的焦点,则弦![]() 的斜率为 ( )
的斜率为 ( )
A. ![]() B.
B. ![]() C.
2 D. 1
C.
2 D. 1
|
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
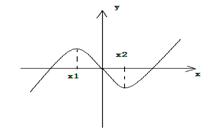 11.函数
11.函数![]()
![]()
|
A.![]() B.
B.![]()
C.![]() D.
D.![]()
12.已知两点M(-5,0),N(5,0),若直线上存在点P ,使![]() ,则称该直线为“B型直线”给出下列直线 ①
,则称该直线为“B型直线”给出下列直线 ①![]() ②
②![]() ③
③![]()
④![]() 其中为“B型直线”的是 ( )
其中为“B型直线”的是 ( )
A.①③ B.①② C.③④ D.①④
二、填空题:(本题共4小题,每小题4分,共16分)
13.函数![]() 的导函数是
的导函数是
14.过抛物线![]() 焦点的直线交抛物线于A、B两点,已知
焦点的直线交抛物线于A、B两点,已知![]() ,则AB中点
,则AB中点
的纵坐标为
15.过点E(5,0)且与圆F:![]() 外切的圆的圆心P的轨迹方程是
外切的圆的圆心P的轨迹方程是
16.若函数![]() 在区间
在区间![]() 内是增函数,则实数
内是增函数,则实数![]() 的取值范围是
的取值范围是
三、解答题:(本大题共6小题,共74分)
17.(本题12分)求与曲线![]() :
:![]() 相切,并且与直线
相切,并且与直线![]() :
:![]() 平行的直线方程。
平行的直线方程。
18.(本题12分)椭圆的中心是原点![]() ,它的短轴长为
,它的短轴长为![]() ,相应于焦点
,相应于焦点![]() (
(![]() )的准线
)的准线![]() 与
与![]() 轴相交于点A,
轴相交于点A,![]() ,
,
(1)求椭圆的离心率;
(2)设直线![]() :
:![]() ,若直线
,若直线![]() 与该椭圆相交于B、C两点,且
与该椭圆相交于B、C两点,且![]() ,求
,求![]() 的值。
的值。
19.(本小题满分12分)已知![]() 在区间
在区间![]() 上最大值是5,最小值是-11,求
上最大值是5,最小值是-11,求![]() 的解析式.
的解析式.
20.(本题12分)双曲线C的两条渐近线过坐标原点,且与圆S:![]() 相切.
相切.
(1)求渐近线方程;
(2)圆S的圆心关于渐近线的对称点在双曲线上,求双曲线C的标准方程。
21.(本题13分)已知函数![]()
(1)若![]() 在
在![]() 处取得极值,求
处取得极值,求![]() 的单调增区间;
的单调增区间;
(2)若![]() 在区间
在区间![]() 内有极大值和极小值,求实数
内有极大值和极小值,求实数![]() 的取值范围.
的取值范围.
22.(本题13分)已知点![]() ,点A、B分别在x轴负半轴和y轴上,且
,点A、B分别在x轴负半轴和y轴上,且![]() ·
·![]() =0,点
=0,点![]() 满足
满足![]() ,当点B在y轴上移动时,记点C的轨迹为E。
,当点B在y轴上移动时,记点C的轨迹为E。
(1)求曲线E的方程;
(2)过点Q(1,0)且斜率为k的直线![]() 交曲线E于不同的两点M、N,若D(
交曲线E于不同的两点M、N,若D(![]() ,0),且
,0),且![]() ·
·![]() >0,求k的取值范围。
>0,求k的取值范围。
附加题:(答题正确完整加10分,答错或不答不扣分)
双曲线C的两条渐近线过坐标原点,且与圆S:![]() 相切. 当
相切. 当![]() 时,求双曲线C的离心率e的取值范围。
时,求双曲线C的离心率e的取值范围。
参考答案
一、选择题:
|
二、13.![]() 14.3 15.
14.3 15.![]() 16.
16.![]()
17.解: ![]()
∵所求直线与![]() 平行 ∴所求直线斜率为1
平行 ∴所求直线斜率为1
令![]() 则
则![]() 或
或![]()
∴切点为![]() 或
或![]()
∴所求直线方程为:![]() 或
或![]()
即![]() 或
或![]()
18.解:(1)由短轴长为![]() 可设椭圆的方程为
可设椭圆的方程为![]()
由已知得 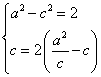 ∴
∴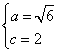
∴![]()
(2)由(1)得椭圆方程为![]() 即
即![]()
由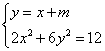 得
得![]()
设![]() 、
、![]() ∴
∴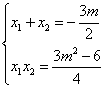
∴![]() ∴
∴![]()
∴![]()
![]() =2
=2
∴![]() ∴
∴![]()
∵![]()
![]()
∴当![]() 时,
时,![]() ∴
∴![]()
19.解: ![]() ∴
∴![]()
由题意可知![]()
令![]() =0,得
=0,得![]()
∵![]()
![]() ∴舍去
∴舍去![]()
(1) 若![]()
|
|
| 0 |
|
|
|
| 0 |
|
|
| ↗ | 极大值 | ↘ |
∵![]()
![]() ∴
∴![]()
![]()
![]() ∴
∴![]()
![]()
若![]()
|
|
| 0 |
|
|
|
| 0 |
|
|
| ↘ | 极小值 | ↗ |
∴![]() ,得
,得![]()
![]()
∴![]()
![]()
20.(1)解:设渐近线方程为:y=kx ∵点(0,2)到直线kx-y=0的距离为1
∴ ![]()
![]() 渐近线方程为:y=
渐近线方程为:y=![]()
(2)m=2时,圆心S(0,2)关于渐近线的对称点S’![]() 在双曲线上,
在双曲线上,
点(0,2)关于![]() 的对称点S’满足
的对称点S’满足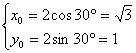
设双曲线C的标准方程为![]() ,则
,则 ![]()
∴所求双曲线标准方程为![]()
21.解:![]()
(1)∵![]() 在
在![]() 处取得极值 ∴
处取得极值 ∴![]()
∴![]() ∴
∴![]()
∴![]()
![]()
令![]() 则
则![]() ∴
∴![]() 或
或![]()
∴函数![]() 的单调递增区间为
的单调递增区间为![]()
(2) ∵![]() 在
在![]() 内有极大值和极小值 ∴
内有极大值和极小值 ∴![]() 在
在![]() 内有两根
内有两根
对称轴![]()
∴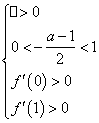 即
即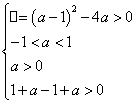 ∴
∴![]()
22.解:(1)设![]()
则![]()
∵![]()
![]()
∴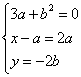 消去
消去![]() 得
得![]() ∵
∵![]() ∴
∴![]()
故曲线E的方程为![]()
(2)设直线![]() 方程为
方程为![]()
由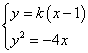 得
得![]()
∵直线![]() 交曲线E于不同的两点M、N ∴
交曲线E于不同的两点M、N ∴![]()
即![]() ∴
∴![]() ①
①
设M![]() ,N
,N![]()
则![]()
∴ 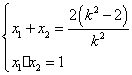
∴![]()
![]()
![]()
![]() 解得
解得![]() ②
②
①②联立解得 ![]() 或
或![]()
附加题:解:①当双曲线焦点在x轴上时,设其方程为:![]()
渐近线方程:![]() 设
设![]()
![]()
∴![]()
![]()
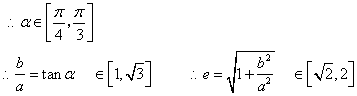
②当双曲线焦点在y轴上时,设其标准方程为:![]()
渐近线方程:![]() 设
设![]()
![]()
∴![]()
![]()
∴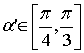
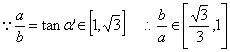
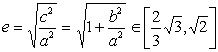
![]()