高二数学第一学期期末试卷
满分100分,考试时间90分钟
| 题号 | 一 | 二 | 三 | 总分 | |||
| 分数 | 15 | 16 | 17 |
18 | |||
| 得分 | 评卷人 |
第Ι卷(选择题,共32分)
一、选择题:(本大题共8小题,每小题4分,共32分.在每题给出的四个选项中,只有一项是符合题目要求的.)
(1)如果直线![]() 与直线
与直线![]() 平行,那么系数
平行,那么系数![]() 等于(
)
等于(
)
![]()
![]()
![]()
![]()
![]()
(2)两名同学进行英语听力练习,甲能听懂的概率为![]() ,乙能听懂的概率为0.5 ,则甲、乙二人恰有一人能听懂的概率为(
)
,乙能听懂的概率为0.5 ,则甲、乙二人恰有一人能听懂的概率为(
)
(3)已知x、y满足条件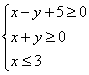 ,则
,则![]() 的最小值为( )
的最小值为( )
A. –6
B.
(4)![]() 的展开式中第四项的系数是( )
的展开式中第四项的系数是( )
A.10 B.
-
(5)抛物线![]() (
(![]() )上横坐标为3的点到焦点的距离是4,则p等于(
)
)上横坐标为3的点到焦点的距离是4,则p等于(
)
A. 8 B.
(6)已知直线![]() 的斜率为
的斜率为![]() ,且过双曲线
,且过双曲线![]() 的左焦点,则直线
的左焦点,则直线![]() 与此双曲线的交点个数为( )个
与此双曲线的交点个数为( )个
A. 3
B.
(7)五个人排成一排,其中甲、乙、丙三人左、中、右顺序不变(不一定相邻)的排法种数是( )
A.12 B.
(8)已知![]() 、
、![]() 是椭圆
是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 是椭圆的右准线,点P
是椭圆的右准线,点P![]() 且在x轴上方,则
且在x轴上方,则![]() 的最大值是( )
的最大值是( )
A.![]() B.30
B.30![]() C.
C.![]() D.
D.![]()
| 得分 | 评卷人 |
二、填空题:(本大题共6小题,每小题4分 ,共24分.答案填在题中横线上.)
(9)在参加2006年德国世界杯足球赛决赛阶段比赛的32支球队中,有欧洲队14支,美洲队8支,亚洲队4支,大洋洲队1支,非洲队5支,从中选出一支球队为欧洲队或美洲队的概率为 .
(10)3个班分别从2个风景点中选择1处游览,有________ 种不同的选法 .
(11)若点(-2,![]() )在不等式2x-3y+6
)在不等式2x-3y+6![]() 0所表示的平面区域内,则
0所表示的平面区域内,则![]() 的取值范围是_________ .
的取值范围是_________ .
(12) 圆![]() 的(
的(![]() 为参数)圆心坐标为 ;直线l与此圆交于A、B两点,且线段AB的中点坐标是
为参数)圆心坐标为 ;直线l与此圆交于A、B两点,且线段AB的中点坐标是![]() ,则直线l的方程为 .
,则直线l的方程为 .
(13)中心在原点,焦点在x轴上,离心率为![]() ,并且虚轴长为8的双曲线标准方程为
,并且虚轴长为8的双曲线标准方程为
__________;若P为此双曲线上的一点,![]() 、
、![]() 分别是此双曲线的左、右焦点,
分别是此双曲线的左、右焦点,
且![]() ,则
,则![]() 的面积为
.
的面积为
.
(14)过椭圆![]() 的右焦点作x轴的垂线交椭圆于A,B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A,B两点,则双曲线的离心率e为
的右焦点作x轴的垂线交椭圆于A,B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A,B两点,则双曲线的离心率e为
.
三、解答题:(本大题共4小题,共44分,解答应写出文字说明,证明过程或演算步骤.)
| 得分 | 评卷人 |
(本题满分12分)
(15)已知点P(2,0),![]() C:
C:![]() .
.
(Ⅰ)当直线l过点P且与圆心C的距离为1时,求直线l的方程;
(Ⅱ)设过点P的直线与![]() C交于A、B两点,且
C交于A、B两点,且![]() ,求以线段AB为直径的圆的方程.
,求以线段AB为直径的圆的方程.
| 得分 | 评卷人 |
(本题满分10分)
(16)一个小朋友将七支颜色各不相同的彩笔排成一列.
(Ⅰ)求红色彩笔与黄色彩笔相邻的概率;
(Ⅱ)求绿色彩笔与蓝色彩笔之间恰有一支彩笔的概率.
| 得分 | 评卷人 |
(本题满分12分)
(17)一次小测验共有3道选择题和2道填空题,每答对一道题得20分,答错或不答得0分.某同学答对每道选择题的概率均为0.8,答对每道填空题的概率均为0.5.各道题答对与否互不影响.
(Ⅰ)求该同学恰好答对1道选择题和2道填空题的概率;
(Ⅱ)求该同学至少答对1道题的概率;
(Ⅲ)求该同学在这次测验中恰好得80分的概率.
| 得分 | 评卷人 |
(本题满分10分普通校学生做,重点校学生不做)
(18)已知两点![]() ,动点
,动点![]() 在
在![]() 轴上的射影为
轴上的射影为![]() 是2和
是2和![]() 的等比中项.
的等比中项.
(I)求动点P的轨迹方程;
(Ⅱ)若直线![]() 交以点M、N为焦点的双曲线C的右支于点Q,求实轴长最长的双曲线C的方程.
交以点M、N为焦点的双曲线C的右支于点Q,求实轴长最长的双曲线C的方程.
| 得分 | 评卷人 |
(本题满分10分重点校学生做,普通校学生不做)
(18)已知椭圆![]() 的左、右焦点分别是
的左、右焦点分别是![]() ,Q是椭圆外的动点,满足
,Q是椭圆外的动点,满足![]() 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,并且满足![]()
(I)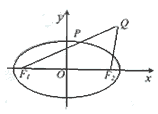 设
设![]() 为点P的横坐标,求证:
为点P的横坐标,求证:![]() ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)在点T的轨迹C上,是否存在点M,
使△F1MF2的面积S=![]() 若存在,求∠F1MF2
若存在,求∠F1MF2
的正切值;若不存在,请说明理由.
草 稿 纸
高二数学学科期末试卷答案
一.选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 答案 | D | C | A | B | C | C | B | B |
二.填空题
9.![]() 10 .8 11.
10 .8 11. ![]() 12. (0,1);
12. (0,1); ![]() 13.
13.![]() ;16
;16
14. ![]() (注12,13小题每空2分)
(注12,13小题每空2分)
三.解答题
15. (Ⅰ)解:设直线l的斜率为k(若k存在),则方程为 ![]() …(2分)
…(2分)
又![]() C的圆心为C(3,-2) , r=3,由
C的圆心为C(3,-2) , r=3,由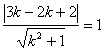
![]() , …… (4分)
, …… (4分)
直线l的方程为![]() ,即
,即![]() ………(5分)
………(5分)
当k不存在时,l的方程为x=2. ………… (7分)
(Ⅱ)依题意AB![]() CP ,得P为线段AB的中点,即为以AB为直径的圆的圆心……(9分)
CP ,得P为线段AB的中点,即为以AB为直径的圆的圆心……(9分)
已知C(3,-2) ,P(2,0),由两点间距离公式得![]() .
…… (10分)
.
…… (10分)
在直角三角形![]() 中,可求半径
中,可求半径![]() .
…………(11分)
.
…………(11分)
故以AB为直径的圆的方程为![]() .
…………(12分)
.
…………(12分)
16.解:七支彩笔可排列总数为![]() ,每一种排列出现的机会是等可能的 …………(3分)
,每一种排列出现的机会是等可能的 …………(3分)
(Ⅰ)记红色彩笔与黄色彩笔相邻为事件A,红色彩笔与黄色彩笔相邻的排列有![]() 种,
种,
则P(A)=![]() .
……………… (7分)
.
……………… (7分)
(Ⅱ)记绿色彩笔与蓝色彩笔之间恰有一支彩笔的事件为B,则
绿色彩笔与蓝色彩笔之间恰有一支彩笔的概率为![]() . … (10分)
. … (10分)
(注:学生(1)问求出红色彩笔与黄色彩笔相邻的概率可得满分,未写出是等可能的不扣分)
17. 解:(Ⅰ)该同学恰好答对1道选择题和2道填空题的概率为
![]() . ……………… (4分)
. ……………… (4分)
(Ⅱ)该同学至少答对1道题的概率为![]() . ……… (8分)
. ……… (8分)
(Ⅲ)设该同学在这次测验中恰好得80分为事件A,他恰好答对2道选择题和
2道填空题为事件B1,他恰好答对3道选择题和1道填空题为事件B2
则A=B1+B2,B1,B2为互斥事件.
![]()
=![]() ……(12分)
……(12分)
18. A(普通校)
解:(Ⅰ)动点为![]() ,则
,则![]()
…………………………… (2分)
∴![]() ,且
,且![]() .
…………………………… (4分)
.
…………………………… (4分)
由题意得![]() ,即
,即![]() ,
,![]() . …… (5分)
. …… (5分)
![]() 是2和
是2和![]() 的等比中项,点P不能与点H重合,
的等比中项,点P不能与点H重合,![]() .
.
∴![]() (
(![]() )为所求点P的轨迹方程. ………………………… (6分)
)为所求点P的轨迹方程. ………………………… (6分)
(Ⅱ)当直线![]() 与双曲线C右支交于点Q时,而
与双曲线C右支交于点Q时,而![]() 关于直线
关于直线![]()
的对称点为![]() ,则
,则![]()
∴双曲线C的实轴长![]() (当且仅当
(当且仅当
Q,E,M共线时取“=”),此时,实轴长![]() 最大为
最大为![]() ;……………… (8分)
;……………… (8分)
所以,双曲线C的实半轴长为![]()
又∵![]() ,∴
,∴![]()
∴双曲线C的方程为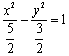 . …………………………… (10分)
. …………………………… (10分)
18.B(重点校)
解:(Ⅰ)证明:设点P的坐标为![]() 椭圆的左准线方程为
椭圆的左准线方程为![]() .
.
由椭圆第二定义得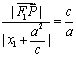 ,即
,即![]()
由![]() ,所以
,所以![]() …………… 3分
…………… 3分
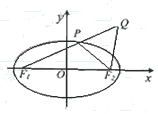 (Ⅱ)解法一:设点T的坐标为
(Ⅱ)解法一:设点T的坐标为![]()
当![]() 时,由
时,由![]() ,
,
得![]() .又由椭圆定义得
.又由椭圆定义得![]() ,如图可得
,如图可得![]()
则![]() ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中,![]() ,所以有
,所以有![]() ………5分
………5分
当![]() 时,点(
时,点(![]() ,0)和点(-
,0)和点(-![]() ,0)在轨迹上.
,0)在轨迹上.
综上所述,点T的轨迹C的方程是![]() …………………6分
…………………6分
解法二:设点T的坐标为![]()
当![]() 时,由
时,由![]() ,得
,得![]() .
.
又![]() ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
设点Q的坐标为(![]() ),则
),则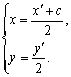
因此![]() ①
①
由![]() 得
得![]() ②
②
将①代入②,可得![]() ………………5分
………………5分
当![]() 时,点(
时,点(![]() ,0)和点(-
,0)和点(-![]() ,0)在轨迹上.
,0)在轨迹上.
综上所述,点T的轨迹C的方程是![]() ………………6分
………………6分
|
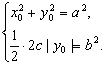
由③得![]() ,由④得
,由④得![]() 所以,当
所以,当![]() 时,存在点M,使S=
时,存在点M,使S=![]() ;
;
当![]() 时,不存在满足条件的点M.
…………………8分
时,不存在满足条件的点M.
…………………8分
当![]() 时,
时,![]() ,
,
由![]() ,
,
![]() ,
,
![]() ,得
,得![]() ……10分
……10分
解法二:
由上解法当![]() 时,存在点M,使S=
时,存在点M,使S=![]() ;
;
当![]() 时,不存在满足条件的点M.
………………………8分
时,不存在满足条件的点M.
………………………8分
当![]() 时,
时,
![]() ,
,![]() ,由
,由![]() ,知
,知![]() ,
,
所以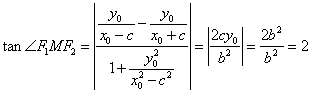 . ………10分
. ………10分