高中二年级理科数学下期期末考试试卷
(理科)
考试时间:120分钟 总分:150分
命题人:刘 波 审题人:钟 波
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。试题卷1至4页。答题卷5到8页。考试结束后,将答题卷和答题卡一并交回。
第Ⅰ卷
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A、B互斥,那么 球是表面积公式
![]()
![]()
如果事件A、B相互独立,那么 其中R表示球的半径
![]() 球的体积公式
球的体积公式
如果事件A在一次试验中发生的概率是P,那么 ![]()
n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
![]()
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知直线![]() 、
、![]() 和平面
和平面![]() ,则
,则![]() 的一个必要不充分的条件是
( )
的一个必要不充分的条件是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 、
、![]() 与
与![]() 成等角
成等角
2、从甲、乙等![]() 名同学中挑选
名同学中挑选![]() 名参加某项公益活动,要求甲、乙中至少有
名参加某项公益活动,要求甲、乙中至少有![]() 人参加,则不同的挑选方法共有
( )
人参加,则不同的挑选方法共有
( )
(A)140种 (B)112种 (C)168种 (D)70种
3、已知![]() 平面
平面![]() ,
,![]() 为垂足,
为垂足,![]() 为斜线
为斜线![]() 在平面
在平面![]() 内的射影,
内的射影,![]() ,
,![]() ,
,![]() ,则
,则![]() 和平面
和平面![]() 所成的角为
( )
所成的角为
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、![]() 的展开式中x的系数是
( )
的展开式中x的系数是
( )
A.-4
B.
5、设有直线m、n和平面![]() 、
、![]() 。下列四个命题中,正确的是
( )
。下列四个命题中,正确的是
( )
A.若m∥![]() ,n∥
,n∥![]() ,则m∥n B.若m
,则m∥n B.若m![]()
![]() ,n
,n![]()
![]() ,m∥
,m∥![]() ,n∥
,n∥![]() ,则
,则![]() ∥
∥![]()
C.若![]()
![]()
![]() ,m
,m![]()
![]() ,则m
,则m![]()
![]() D.若
D.若![]()
![]()
![]() ,m
,m![]()
![]() ,m
,m![]()
![]() ,则m∥
,则m∥![]()
6、设随机变量![]() 服从正态分布N(0,1) ,若P (
服从正态分布N(0,1) ,若P (![]() >c+1)=P(
>c+1)=P(![]() <c-
<c-![]() ,则c=
( )
,则c=
( )
A.-1 B
7、一个盒子里装有相同大小的红球、白球共![]() 个,其中白球
个,其中白球![]() 个,从中任取
个,从中任取![]() 个,则概率为
个,则概率为![]() 的事件是
( )
的事件是
( )
A.没有白球 B.至少有一个白球 C.至少有一个红球 D.至多有一个白球
8、某班举行联欢会,原定的6个节目已排出节目单,演出前又增加了3个节目,若将这3个节目插入原节目单中,则不同的插法总数为 ( )
A.504 B.210 C.336 D.378
9、5张卡片上分别写有A,B,C,D,E 5个字母,从中任取2张卡片,这两张卡片上的字母恰好是按字母顺序相邻的概率为 ( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
10、有8张卡片分别标有数字1,2,3,4,5,6,7,8,从中取出6张卡片排成3行2列,要求3行中仅有中间行的两张卡片上的数字之和为5,则不同的排法共有 ( )
(A) 1344种 (B) 1248种 (C) 1056种 (D) 960种
11、长方体ABCD-A1B1C1D1的8个顶点在同一球面上,且AB=2,AD=![]() ,AA1=1,则顶点A、B间的球面距离是
( )
,AA1=1,则顶点A、B间的球面距离是
( )
A.2![]() B.
B.![]() C.
C.![]() D.
D.
![]()
12、三位数中,如果十位上的数字比百位上的数字和个位上的数字都大,则称这个数为凸数,如![]() 等,那么任取一个三位正整数恰好是无重复数字的三位凸数的概率是
( ).
等,那么任取一个三位正整数恰好是无重复数字的三位凸数的概率是
( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在答题卷中相应横线上。
13、某高中共有学生1200人,其中高一年级有500人,高二年级有400人,高三年级有300人,采用分层抽样方法抽取一个容量为60的样本,那么高一、高二、高三各年级抽取学生个数分别应为_______________________.
14、将正方形![]() 沿对角线
沿对角线![]() 折成一个直二面角,则异面直线AB和CD所成的角为__________________.
折成一个直二面角,则异面直线AB和CD所成的角为__________________.
15、一个四面体的所有棱长都为![]() ,四个顶点在同一个球面上,则此球的体积为___________________.
,四个顶点在同一个球面上,则此球的体积为___________________.
16、若![]()
![]() 展开式的各奇项系数之和为32,则n= ,其展开式中的常数项为
展开式的各奇项系数之和为32,则n= ,其展开式中的常数项为
。(用数字作答)
三、解答题(共74分,解答应写出文字说明,证明过程或演算步骤.)
17、(10分)已知![]() 展开式中的前三项系数成等差数列,
展开式中的前三项系数成等差数列,
求展开式中含![]() 的项
的项
18、(本小题共12分)
甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加A岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
19、(本小题共13分)
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.
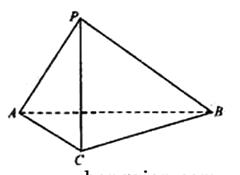
(Ⅰ)求证:PC⊥AB;
(Ⅱ)求二面角B-AP-C的大小;
(Ⅲ)求点C到平面APB的距离.
20、(本小题满分13分)
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
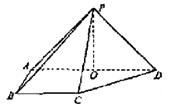
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
21.、本小题满分12分)
袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一球.ξ表示所取球的标号.
(Ⅰ)求ξ的分布列,期望和方差;
(Ⅱ)若η=aξ![]() ,Eη=1,Dη=11,试求a,b的值.
,Eη=1,Dη=11,试求a,b的值.
22、(本小题满分14分)
在数列{an},{bn}中,a1=2, b1=4,且![]() 成等差数列,
成等差数列,![]() 成等比数列(
成等比数列(![]() )
)
(Ⅰ)求a2, a3, a4及b2, b3, b4,由此猜测{an},{bn}的通项公式,并证明你的结论;
(Ⅱ)证明:![]()
成都十八中2007~2008学年度下期高中二年级
期末考试数学答题卷(理科)
二、填空题:本大题共4小题,每小题4分,满分16分.把答案填在题中横线上.
13、 14.
15. 16.
三、解答题(共74分,解答应写出文字说明,证明过程或演算步骤.)
17、(10分)
已知![]() 展开式中的前三项系数成等差数列,求展开式中含
展开式中的前三项系数成等差数列,求展开式中含![]() 的项
的项
18、(本小题共12分)
甲、乙等五名奥运志愿者被随机地分到A,B,C,D四个不同的岗位服务,每个岗位至少有一名志愿者.
(Ⅰ)求甲、乙两人同时参加A岗位服务的概率;
(Ⅱ)求甲、乙两人不在同一个岗位服务的概率;
(Ⅲ)设随机变量ξ为这五名志愿者中参加A岗位服务的人数,求ξ的分布列.
19、(本小题共13分)
如图,在三棱锥P-ABC中,AC=BC=2,∠ACB=90°,AP=BP=AB,PC⊥AC.

(Ⅰ)求证:PC⊥AB;
(Ⅱ)求二面角B-AP-C的大小;
(Ⅲ)求点C到平面APB的距离.
20、(本小题满分13分)
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
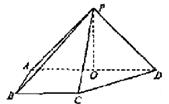
(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的大小;
(Ⅲ)线段AD上是否存在点Q,使得它到平面PCD的距离为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
21.、本小题满分12分)
袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4).现从袋中任取一球.ξ表示所取球的标号.
(Ⅰ)求ξ的分布列,期望和方差;
(Ⅱ)若η=aξ-b,Eη=1,Dη=11,试求a,b的值.
22、(本小题满分14分)
在数列{an},{bn}中,a1=2, b1=4,且![]() 成等差数列,
成等差数列,![]() 成等比数列(
成等比数列(![]() )
)
(Ⅰ)求a2, a3, a4及b2, b3, b4,由此猜测{an},{bn}的通项公式,并用数学归纳法证明你的结论;
(Ⅱ)证明:![]()
高二理科六月考数学参考答案
一、选择题(每小题5分共60分)
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | C | A | D | B | B | A | B | C | C | B |
二、填空题(每小题4分16分)
13. 25,20,15; 14. ![]() 15.
15. ![]() ;
16. 16
;
16. 16
三、解答题(共74分,解答应写出文字说明,证明过程或演算步骤.)
17、(10分)解: ![]()
得前三项系数分别是![]() ,
,![]() ,
,![]()
前三项系数成等差数列,![]() 有
有![]()
解得![]() 或
或![]() (不合题意舍去)
(不合题意舍去)
![]()
由![]() 得
得![]()
![]() 所求项是
所求项是![]()
18、(12分)解:(Ⅰ)记甲、乙两人同时参加A岗位服务为事件EA,那么
P(EA)=![]() 即甲、乙两人同时参加A岗位服务的概率是
即甲、乙两人同时参加A岗位服务的概率是![]()
(Ⅱ)记甲、乙两个同时参加同一岗位服务为事件E,那么
P(E)=![]() 所以,甲、乙两人不在同一岗位服务的概率是
所以,甲、乙两人不在同一岗位服务的概率是
P(![]() )=1-P(E)=
)=1-P(E)=![]()
(Ⅲ)随机变量ξ可能取的值为1,2.事件“ξ=2”是指有两人同时参加A岗位服务,则
P(ξ=2)=![]()
所以p(ξ-1)=1-P(ξ=2)=![]() .ξ的分布列是
.ξ的分布列是
| ξ | 1 | 2 |
P |
|
|
19、解法一:
(I) 取AB中点D,连结PD,CD.
∵AP=BP,∴PD⊥AB. ∵AC=BC, ∴CD⊥AB.
∵PD∩CD=D, ∴AB⊥平面PCD. ∵PC∩平面PCD. ∴PC⊥AB.
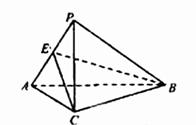 (Ⅱ)∵AC=BC,AP=BP,
(Ⅱ)∵AC=BC,AP=BP,
∴△APC≌△BPC.
又PC⊥BC. ∴PC⊥BC.
又∠ACB=90°,即AC⊥BC.
且AC∩PC=C, ∴BC⊥平面PAC.
取AP中点E,连结BE,CE.
∵AB=BP, ∴BE⊥AP.
∵EC是BE在平面PAC内的射影. ∴CE⊥AP.
∴∠BEC是二面角B-AP-C的平面角.
在△BCE中,∠BCE=90°,BC=2,BE=![]() AB=
AB=![]() ,∴sin∠BEC=
,∴sin∠BEC=![]()
∴二面角B-AP-C的大小为 aresin![]()
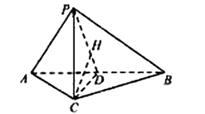 (Ⅲ)由(Ⅰ)知AB⊥平面PCD,
(Ⅲ)由(Ⅰ)知AB⊥平面PCD,
∴平面APB⊥平面PCD.过C作CH⊥PD,垂足为H.
∵平面APB∩平面PCD=PD,∴CH⊥平面APB.
∴CH的长即为点C到平面APB的距离,
由(Ⅰ)知PC⊥AB,又PC⊥AC,
且AB∩AC=A.∴PC⊥平面ABC.
CD![]() 平面ABC.∴PC⊥CD.
平面ABC.∴PC⊥CD.
在Rt△PCD中,CD=![]()
∴PC=![]() ∴CH=
∴CH=![]() ∴点C到平面APB的距离为
∴点C到平面APB的距离为![]()
解法二:
(Ⅰ)∵AC=BC,AP=BP,∴△APC≌△BPC.
又PC⊥AC.∴PC⊥BC.∵AC∩BC=C,∴PC⊥平面ABC.∵AB![]() 平面ABC,∴PC⊥AB.
平面ABC,∴PC⊥AB.
(Ⅱ)如图,以C为原点建立空间直角坐标系C-xyz.
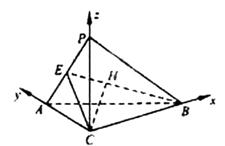 则C(0,0,0),A(0,2,0),B(2,0,0).
则C(0,0,0),A(0,2,0),B(2,0,0).
设P(0,0,1).
∵|PB|=|AB|=2![]() ,∴t=2,P(0,0,2).取AP中点E,连结BE,CE.
,∴t=2,P(0,0,2).取AP中点E,连结BE,CE.
∵|AC|=|PC|,|AB|=|BP|,∴CE⊥AP,BE⊥AP.∴∠BEC是二面角B-AP-C的平面角.
∵E(0,1,1),![]() ∴cos∠BEC=
∴cos∠BEC=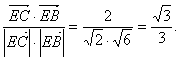
∴二面角B-AP-C的大小为arecos![]()
(Ⅲ)∵AC=BC=PC,
∴C在平面APB内的射影为正△APB的中心H,且CH的长为点C到平面APB的距离.
如(Ⅱ)建立空间直角坐标第C-xyZ.
∵![]() ∴点H的坐标为(
∴点H的坐标为(![]() ).∴
).∴![]() ∴点C到平面APB的距离为
∴点C到平面APB的距离为![]()
20 解法一:
(Ⅰ)证明:在△PAD中PA=PD,O为AD中点,所以PO⊥AD,
又侧面PAD⊥底面ABCD,平面![]() 平面ABCD=AD,
平面ABCD=AD, ![]() 平面PAD,
平面PAD,
所以PO⊥平面ABCD.
(Ⅱ)连结BO,在直角梯形ABCD中、BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,所以四边形OBCD是平行四边形,
所以OB∥DC.
由(Ⅰ)知,PO⊥OB,∠PBO为锐角,
所以∠PBO是异面直线PB与CD所成的角.
因为AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,所以OB=![]() ,
,
在Rt△POA中,因为AP=![]() ,AO=1,所以OP=1,
,AO=1,所以OP=1,
在Rt△PBO中,tan∠PBO=![]()
所以异面直线PB与CD所成的角是![]() .
.
(Ⅲ)假设存在点Q,使得它到平面PCD的距离为![]() .
.
设QD=x,则![]() ,由(Ⅱ)得CD=OB=
,由(Ⅱ)得CD=OB=![]() ,
,
在Rt△POC中, ![]() 所以PC=CD=DP,
所以PC=CD=DP, ![]()
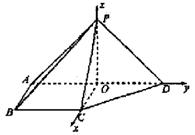 由Vp-DQC=VQ-PCD,得
由Vp-DQC=VQ-PCD,得![]() 2,所以存在点Q满足题意,此时
2,所以存在点Q满足题意,此时![]() .
.
解法二:
(Ⅰ)同解法一.
(Ⅱ)以O为坐标原点,![]() 的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz,依题意,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),
的方向分别为x轴、y轴、z轴的正方向,建立空间直角坐标系O-xyz,依题意,易得A(0,-1,0),B(1,-1,0),C(1,0,0),D(0,1,0),
P(0,0,1),
所以![]() 所以异面直线PB与CD所成的角是arccos
所以异面直线PB与CD所成的角是arccos![]() ,
,
(Ⅲ)假设存在点Q,使得它到平面PCD的距离为![]() ,由(Ⅱ)知
,由(Ⅱ)知![]()
设平面PCD的法向量为n=(x0,y0,z0).则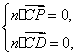 所以
所以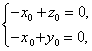 即
即![]() ,
,
取x0=1,得平面PCD的一个法向量为n=(1,1,1).
设![]() 由
由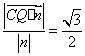 ,得
,得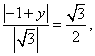 解y=-
解y=-![]() 或y=
或y=![]() (舍去),此时
(舍去),此时![]() ,所以存在点Q满足题意,此时
,所以存在点Q满足题意,此时![]() .
.
21、17.本小题主要考查概率、随机变量的分布列、期望和方差等概念,以及基本的运算能力.(满分12分)解:(Ⅰ)![]() 的分布列为:
的分布列为:
|
| 0 | 1 | 2 | 3 | 4 |
| P |
|
|
|
|
|
∴![]()
D![]() (Ⅱ)由
(Ⅱ)由![]() ,得a2×2.75=11,即
,得a2×2.75=11,即![]() 又
又![]() 所以
所以
当a=2时,由1=2×1.5![]() ,得b=2; 当a=-2时,由1=-2×1.5
,得b=2; 当a=-2时,由1=-2×1.5![]() ,得b=
,得b=![]() . ∴
. ∴![]() 或
或![]() 即为所求.
即为所求.
22、(14分)本小题主要考查等差数列,等比数例,数学归纳法,不等式等基础知识,考查综合运用数学知识进行归纳、总结、推理、论证等能力.满分12分.
解:(Ⅰ)由条件得![]()
由此可得![]() 猜测
猜测![]()
用数学归纳法证明:
①当n=1时,由上可得结论成立.
②假设当n=k时,结论成立,即
![]() 那么当n=k+1时,
那么当n=k+1时,
![]()
所以当n=k+1时,结论也成立.
由①②,可知![]() 对一切正整数都成立.
对一切正整数都成立.
(Ⅱ)![]() n≥2时,由(Ⅰ)知
n≥2时,由(Ⅰ)知![]()
故![]()
=![]()
=![]()
综上,原不等式成立.