高二学业水平测试数学模拟试题2
一、选择题。本卷共18小题，每小题3分，共54分．在每小题给出的四个选项中，只有一项是符合题目要求的，请把符合要求的选项填写在后面的答题卡中．
1．设全集I=R，集合P=
，集合Q={ x x+4>0}，则 （ ）
A 
P
Q=Æ BP
Q=R C
Q= D
={-4}
2 若
，则点
位于（ ）
A第一象限 B第二象限 C第三象限
D第四象限
3 有一个几何体的三视图及其尺寸如下（单位
），则该几何体的表面积及体积为：（
）
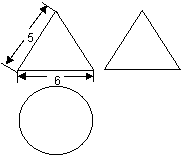A
，
B
，
C
，
D 以上都不正确
4．
是定义在R上的以3为周期的偶函数，且
，则方程=0在区间（0，6）内解的个数的最小值是 （ ）
A．5 B．
5
将参加数学竞赛的1000名学生编号如下0001，0002，0003，…，1000，打算从中抽取一个容量为50的样本，按系统抽样的方法分成50部分，如果第一部分的编号为0001，0002，0003，…，0020，从第一部分随机抽取一个号码为0015，则被抽取的第40个号码为（ ）
A．0040 B．
6若平面四边形ABCD满足
且
，则该四边形一定是（ ）
A 直角梯形 B 矩形
C 菱形 D 正方形
7下面程序的功能是（ ）
A 统计十个数据中负数个数 B
找出十个数据中的负数
C 判断x的符号 D
求十个数据中所有负数的和
8
如图，边长为2的正方形中有一封闭曲线围成的阴影区域，在正
方形中随机撒一粒豆子（假设它落在正方形区域内任何位置的机会均等），它落在阴影区域内的概率为
，则阴影区域的面积为（ ）
A．
B．
C． D．无法计算
9．不等式
恒成立，则
的取值范围为( )
A．
B．
C．
D．
10 在等差数列
中
，且
，则使数列前n项和
取最小值的n等于( )
A 5 B 7 D 8
11．已知f(x)=2
x+1，则
的值是 （ ）
A
B 
C
D
5
12．函数
的值域是 （ ）
A
[-2，2] B
[-1，2] C
[-1，1] D
[0，2]
13若
=
，
，则
的值为 （ ）
A
1
B
D
14．已知函数
，则函数的图像的一条对称轴方程是（ ）
Ａ 
Ｂ 
Ｃ 
Ｄ 
15 设函数
，若是奇函数，则
的值是（ ）
A 
B 
C 
D 4
16把圆
平分，且不通过第四象限的直线的斜率的取值范围是 （ ）
A 
B 
C 
D 
17．在正四面体
中，D,E,F分别是
的中点，下面四个结论中不成立的是（ ）
A 
B
C 
D
18 若圆锥侧面展开图是圆心角为
的扇形，则这个圆锥的表面积与侧面积的比是
（ ）
A 3：2 B 2： 4：3 D 5：3
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 答案 |
二、填空题：本大题共4小题，每小题4分，共16分
19 圆心在
轴上，通过点（3，1）且与
轴相切的圆的方程是
。
20 两平行线
之间的距离为
，则
21下列各族向量
①
②
③
其中能作为表示它们所在平面内的所有向量的基底的是
。
22 已知是定义在R上的函数，且满足
，当
有
，现有三个命题：①是以2为周期的函数；②当
时，
；③是偶函数。其中正确的序号是
。
三、解答题：本大题共3小题，共30分 解答应写出文字说明，证明过程或演算步骤
23．平面向量
，若存在不同时为
的实数
和
，使
且
，试求函数关系式
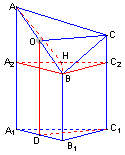
24右图是一个直三棱柱（以
为底面）被一平面所截得到的几何体，截面为
已知
，
，
，
，
（1）设点
是
的中点，证明：
平面；
（2）求与平面
所成的角的大小；
（3）求此几何体的体积
25．已知函数
⑴当
，解不等式
；
⑵讨论的奇偶性，并说明理由
学业水平测试模拟试题2答案
一选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 答案 | D | D | A | B | B | C | A | B | D | B | A | B | B | B | A | D | C | C |
二、填空题
19、
20、-1或1 21、① 22、①②
三、解答题
23、解：由得
24、解法一：
（1）证明：作
交
于
，连
则
，
因为是的中点，
所以
则
是平行四边形，因此有
，
平面
，且
平面
则面
（2）解：如图，过
作截面
面，分别交
，
于
，
，
作
于
，
因为平面
平面，则
面
连结
，则
就是与面所成的角
因为
，
，所以
与面所成的角为
（3）因为，所以
所求几何体的体积为
25、
解：⑴
⑵当
时，，对任意的
，
，
是偶函数
当
时 
，取
得
，
，
函数既不是奇函数也不是偶函数。