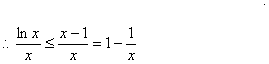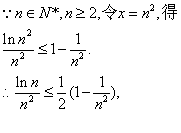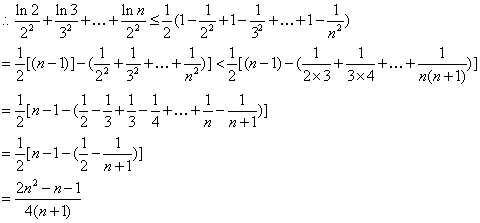高二年级数学第二学期综合练习
（考试时间120分钟，试卷满分150分）
一、填空题：本大题共14小题，每小题5分，共70分．
1．命题“对任意的
”的否定是
2．复数
=
3．“
”是“对任意的正数
，
”的 条件
4．设集合
，则
的取值范围是
5．为得到函数
的图像，只需将函数
的图像
6．已知t为常数，函数
在区间[0，3]上的最大值为2，则t=
7．
= ．
8．已知实数x,y满足条件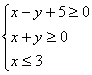
，
为虚数单位），则
的最大值和最小值分别是
9．已知
，则
=
10．若动直线
与函数
和
的图像分别交于
两点，则
的最大值为
11．设函数
，则
的单调增区间为
12．若函数
的图像与函数
的图像关于直线
对称，则
13．已知函数
是R上的偶函数，且在区间
上是增函数.令
，则a、b、c的大小关系由小到大排列为
14．设奇函数在
上为增函数，且
，则不等式
的解集为
二、解答题：解答应写出文字说明，证明过程或演算步骤．
15．（14分）已知函数f(x)＝
为偶函数，且函数y＝f(x)图象的两相邻对称轴间的距离为
（Ⅰ）求f（
）的值；
（Ⅱ）将函数y＝f(x)的图象向右平移
个单位后，再将得到的图象上各点的横坐标伸长到原来的4倍，纵坐标不变，得到函数y＝g(x)的图象，求g(x)的单调递减区间。
16．（14分）设全集U＝R
（1）解关于x的不等式
（
R）
（2）记A为（1）中不等式的解集，集合B＝｛
｝，若
恰有3个元素，求a的取值范围。
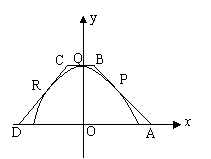
17．（14分）如图，等腰梯形
的三边
分别与函数
，
的图象切于点
.求梯形面积的最小值。
18．（16分）已知函数
.
（1）若
，求的值；
（2）若
对于
恒成立，求实数
的取值范围。
19．（16分）已知是实数，函数
。
（Ⅰ）求函数的单调区间；
（Ⅱ）设
为在区间
上的最小值。
（i）写出的表达式；（ii）求的取值范围，使得
。
20. （16分）设
（e为自然对数的底数）
（1）求p与q的关系；
（2）若
在其定义域内为增函数，求p的取值范围；
（3）证明：
①
；②
（n∈N，n≥2）
答案：
1．
2．－8i
3．充分不必要条件
4．
5．
只需将函数的图像向左平移
个单位得到函数的图像
6．1
7．2
8．
9．
10．
11．
（
）
12．由
13．
14．由奇函数可知
，而，则
，当
时，
；当
时，
，又在上为增函数，则奇函数在
上为增函数，
15．（Ⅰ）f(x)＝
＝
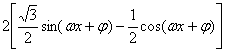
＝2sin(
-)
因为 f(x)为偶函数，
所以 对x∈R,f(-x)=f(x)恒成立，
因此 sin（--）＝sin(-).
即-sin
cos(
-)+cossin(-)=sincos(-)+cossin(-),
整理得 sincos(-)=0.因为 
＞0，且x∈R,所以 cos（-）＝0.
又因为 0＜＜π，故 -＝
.所以 f(x)＝2sin(+)=2cos.
由题意得 
故 f(x)=2cos2x.
因为 
（Ⅱ）将f(x)的图象向右平移个
个单位后，得到
的图象，再将所得图象横坐标伸长到原来的4倍，纵坐标不变，得到
的图象.
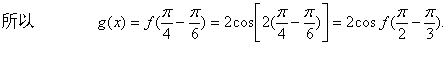
当 2kπ≤
≤2 kπ+ π (k∈Z),
即 4kπ＋≤
≤x≤4kπ+
(k∈Z)时，g(x)单调递减.
因此g(x)的单调递减区间为 
(k∈Z)
16．：(Ⅰ)由x-1+a-1＞0得x-1＞1-a．
当a＞1时，解集是R；
当a≤1时，解集是{xx＜a或x＞2-a}．
(Ⅱ)当a＞1时，
UA=φ；
当a≤1时，UA={xa≤x≤2-a}．
因sin(πx-
)+
cos(πx-)
=2[sin(πx-)cos+cos(πx-)sin]=2sinπx，
由sinπx=0，得πx=kπ(k∈Z)，即x=k∈Z，所以B=Z．
当(UA)∩B恰有3个元素时，a应满足
解得-1＜a≤0．
17．解：设梯形的面积为
，点P的坐标为
。由题意得，
点
的坐标为
，直线
的方程为
。
直线
的方程为
即：
令
得，
令 得，
当且仅当
，即
时，取“=”且
，
时，
有最小值为
.
梯形的面积的最小值为。
18．（1）当
时，
；当
时，
.
由条件可知 
，即 
，
解得 
.
，
.
（2）当
时，
，
即 
.
， 
.
，
故
的取值范围是
.
19．（Ⅰ）解：函数的定义域为
，
（）．
若
，则
，
有单调递增区间．
若
，令
，得
，
当
时，
，
当
时，．
有单调递减区间
，单调递增区间
．
（Ⅱ）解：（i）若，在
上单调递增，
所以
．
若
，在上单调递减，在
上单调递增，
所以
．
若
，在上单调递减，
所以
．
综上所述，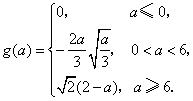
（ii）令
．
若，无解．
若，解得
．
若，解得
．
故的取值范围为
．
20．（1）由题意
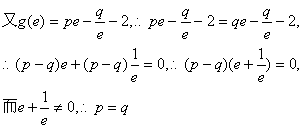
（2）由（1）知：
（x>0）
令h(x)=px2－2x+p.要使g(x)在（0，+∞）为增函数，只需h(x)在（0，+∞）满足：h(x)≥0恒成立.
即px2－2x+p≥0
上恒成立
又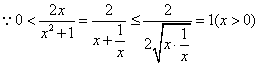
所以
（3）证明：①即证：lnx－x+1≤0 (x>0)，
设
.
当x∈（0，1）时，k′(x)>0，∴k(x)为单调递增函数；
当x∈（1，∞）时，k′(x)<0，∴k(x)为单调递减函数；
∴x=1为k(x)的极大值点，
∴k(x)≤k(1)=0.
即lnx－x+1≤0，∴lnx≤x－1.
②由①知lnx≤x－1,又x>0，
