高二数学下学期六校联考试卷
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共150分,考试用时120分钟。
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.
1.直线![]() 同时经过第一、三、四象限的必要不充分条件是
( )
同时经过第一、三、四象限的必要不充分条件是
( )
A.![]() B.m·n<0
B.m·n<0
C.![]() D.
D.![]()
2.以原点为圆心,且截直线3x+4y+15=0所得弦长为8的圆的方程是 ( ) A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若直线![]() 始终平分圆
始终平分圆![]() 的周长,则
的周长,则![]() 取值范围是
( )
取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.曲线f(x,y)=0关于直线x-y-2=0的对称曲线的方程为 ( )
A.f(y+2,x)=0 B.f (x-2,y)=
5.设点![]() ,
,![]() 若直线
若直线![]() 与线段
与线段![]() 有交点,则
有交点,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.直线![]() 与直线
与直线![]() 互相垂直,则
互相垂直,则![]() 的最小值为 ( )
的最小值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.直线![]() 的方向向量为
的方向向量为![]() ,直线
,直线![]() 的方向向量为
的方向向量为![]() ,那么
,那么![]() 到
到![]() 的角是
( )
的角是
( )
A.20° B.30° C.150° D.160°
8.已知集合![]() ,集合
,集合![]()
![]()
![]() ,那么
,那么![]() 中
( )
中
( )
A.不可能有两个元素 B.至多有一个元素
C.不可能只有一个元素 D.必含无数个元素
9.已知向量![]() ,且
,且![]() 的夹角为钝角,则在
的夹角为钝角,则在![]() 平面上,点
平面上,点![]() 所在的区域是
( )
所在的区域是
( )
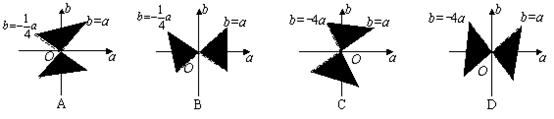
|
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
11.已知两个圆C1:x2+y2=1和C2:(x+5)2+y2=1,如果直线x-![]() y+m=0恰好在这两个圆之间通过,则实数m的取值范围是
( )
y+m=0恰好在这两个圆之间通过,则实数m的取值范围是
( )
A.(1,4) B.(2,3) C.(1,3) D.(2,4)
12.若圆![]() 至少能盖住函数
至少能盖住函数![]() 的一个最大值点和一个最小值点,则
的一个最大值点和一个最小值点,则![]() 的取值范围是
( )
的取值范围是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在答题卡相应位置上.
13.已知直线![]() 与
与![]() 平行,则
平行,则![]() ___________.
___________.
14.过点P(3,7)做圆![]() 的两条切线,切点分别为A、B,则直线AB的方程为
.
的两条切线,切点分别为A、B,则直线AB的方程为
.
15.已知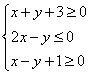 ,则
,则![]() 的最大值为___________.
的最大值为___________.
16.给出下列命题:①若![]() ,
,![]() ,则
,则![]() ; ②若
; ②若![]() ,则
,则![]() ;③设
;③设![]() ,
,![]() ,则直线AB的倾斜角
,则直线AB的倾斜角![]() ;④如果曲线C上的点的坐标
;④如果曲线C上的点的坐标![]() 满足方程
满足方程![]() ,则方程
,则方程![]() 的曲线是C
的曲线是C
其中真命题的序号是_______________.
三、解答题:本大题共6小题,共74分. 解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知A(1,2),B(5,4)和直线x-2y-2=0上一动点P,且点P使|PA|+|PB|最小,求点P的坐标.
18.(本小题满分12分)
设直线l与圆![]() 交于A、B两点,O为坐标原点,已知
交于A、B两点,O为坐标原点,已知![]()
(1)当原点O到直线l的距离为![]() 时,求直线l的方程;
时,求直线l的方程;
(2)当OA⊥OB时,求直线l的方程.
19.(本小题满分12分)
某人上午7:00时,乘摩托车以匀速![]() 千米/时
千米/时![]() 从A港出发到相距
从A港出发到相距![]() 千米/时
千米/时![]() 自B港向距
自B港向距
(1)作图表示满足上述条件的x, y的范围;
(2)如果已知所要的经费:![]() (元),那么
(元),那么![]() ,
, ![]() 分别是多少时所要的经费最少?此时需花费多少元?
分别是多少时所要的经费最少?此时需花费多少元?
20.(本小题满分12分)
已知定点![]() 、
、![]() ,动点
,动点![]() 满足:
满足:![]() 等于点
等于点![]() 到点
到点![]() 距离平方的k倍.
距离平方的k倍.
(1)试求动点![]() 的轨迹方程;
的轨迹方程;
(2)当k=2时,求![]() 最大值和最小值.
最大值和最小值.
21.(本小题满分12分)
已知圆的方程是:![]() ,其中
,其中![]() ,且
,且![]() .
.
(1)求证:![]() 取不为1的实数时,上述圆恒过定点;
取不为1的实数时,上述圆恒过定点;
(2)求恒与圆相切的直线的方程;
(3)求圆心的轨迹方程。
22.(本小题满分14分)
已知圆C:![]() ,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点P(-3,0)
,圆D的圆心D在y轴上,且与圆C外切,圆D与y轴交于A 、B两点,点P(-3,0)
(1)若点D的坐标为(0,3),求![]() 的正切值;
的正切值;
(2)当点D在y 轴上运动时,求![]() 的最大值;
的最大值;
(3)在x轴上是否存在定点![]() ,当圆D在y轴上运动时,
,当圆D在y轴上运动时,![]() 是定值?如果存在,求点
是定值?如果存在,求点![]() 的坐标,如果不存在,说明理由.
的坐标,如果不存在,说明理由.
参考答案:
一、选择题
1.B 2.B 3.D 4.C 5.D 6.B 7.B 8.C 9.A 10.D 11.B 12.A
|
13.-2 14.![]() 15.26 16.①
15.26 16.①
三、解答题
17.解:由题知点A、B在已知直线的同侧,
设点A关于已知直线的对称点为![]()
则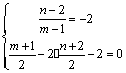 解得
解得![]() 即
即![]()
又![]() , 当且仅当
, 当且仅当![]() 三点共线时取等号
三点共线时取等号
此时直线![]() 的方程为:
的方程为:![]() , 与已知直线方程联立解得P(4,1)
, 与已知直线方程联立解得P(4,1)
18.解:(1)当直线l与x轴垂直时,直线l的方程为:![]()
当直线![]() 与
与![]() 轴不垂直时,可设l:
轴不垂直时,可设l:![]()
![]() 即:
即:![]()
依题意有:![]() ,解得
,解得![]() ,所求直线的方程为:
,所求直线的方程为:![]()
综上:所求直线的方程为:![]() 或
或![]()
(2)由已知![]() ,有
,有![]() ,当
,当![]() 时,原点O到直线l的距离为
时,原点O到直线l的距离为![]() ,可求得直线l的方程为
,可求得直线l的方程为![]()
即![]() 或
或![]()
19.解:(1)依题意得:![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,
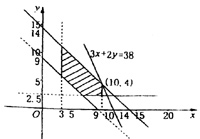 所以
所以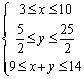 ,所以满足条件的点的范围是图中阴影部分:
,所以满足条件的点的范围是图中阴影部分:
(2)![]() ,
,
![]() ,
,
作出一组平行直线![]() (t为参数),
(t为参数),
由图可知,当直线![]() 经过点
经过点![]() 时,
时,
其在y轴上截距最大,
此时p有最小值,即当![]() 时,p最小,
时,p最小,
此时![]() 元
元
20.解:(1)设![]() (x,y),则,
(x,y),则,
![]()
![]() , 即:
, 即:![]() ,为动点
,为动点![]() 的轨迹方程.
的轨迹方程.
(2)当k=2时,![]()
![]() 点的轨迹方程为,
点的轨迹方程为,![]()
令![]()
又![]() 在圆
在圆![]() 外, 所以
外, 所以
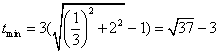 ,
,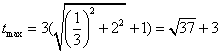 .
.
21.解:(1)将方程![]()
整理得:![]()
令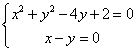 解之得
解之得![]()
![]() 定点为
定点为![]()
(2)圆的圆心坐标为(![]() ,
,![]() ),半径为
),半径为![]()
![]()
显然,满足题意切线一定存在斜率,
![]() 可设所求切线方程为
可设所求切线方程为![]() ,即
,即![]() ,
,
则圆心到直线的距离应等于圆的半径,即![]() 恒成立,
恒成立,
即![]() 恒成立比较系数得
恒成立比较系数得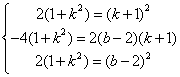
解之得![]() ,所以所求的直线方程为
,所以所求的直线方程为![]()
(3)圆心坐标为(![]() ,2-
,2-![]() ),又设圆心坐标为(x,y),
),又设圆心坐标为(x,y),
则有![]() 消去参数得
消去参数得![]() ,即所求的圆心的轨迹方程为
,即所求的圆心的轨迹方程为![]()
![]() .
.
22.解:(1)∵![]() 且⊙C与⊙D外切,⊙D半径r=3,此时,A、B坐标分别为(0,0),(0,6)
且⊙C与⊙D外切,⊙D半径r=3,此时,A、B坐标分别为(0,0),(0,6)
∵![]() ∴
∴![]()
(2)设![]() 半径为r,则
半径为r,则![]() ,
,
![]() 点坐标分别为
点坐标分别为![]() ,则
,则![]() ,
,![]() ,
,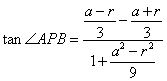 =
=![]() ,
,![]() ,
,
又![]() ,
,![]() 的最大值为
的最大值为![]()
(3)假设存在点![]() ,则
,则![]()
则 .
.
又![]() ,
,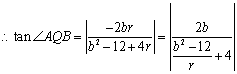 .
.
欲使![]() 的大小与
的大小与![]() 无关,必
无关,必![]() ,
,![]() .
.
此时![]() 即存在.
即存在.