(一).选择题
(1)曲线![]() 在点(1,-1)处的切线方程为( )
在点(1,-1)处的切线方程为( )
A.![]() B。
B。![]() C。
C。![]() D。
D。![]() a
a
(2) 函数y=![]() x2+1的图象与直线y=x相切,则
x2+1的图象与直线y=x相切,则![]() =
( )
=
( )
A.
![]() B.
B.![]() C.
C.![]() D.1
D.1
(3) 函数![]() 是减函数的区间为 ( )
是减函数的区间为 ( )
A.![]() B.
B.![]() C.
C.![]() D.(0,2)
D.(0,2)
(4) 函数![]() 已知
已知![]() 时取得极值,则
时取得极值,则![]() = ( )
= ( )
A.2 B.
(5) 在函数![]() 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于![]() 的点中,坐标为整数的点的个数是 ( )
的点中,坐标为整数的点的个数是 ( )
A.3 B.
(6)函数![]() 有极值的充要条件是 ( )
有极值的充要条件是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(7)函数![]() (
(![]() 的最大值是( )
的最大值是( )
A. ![]() B.
B.
(8)函数![]() =
=![]() (
(![]() -1)(
-1)(![]() -2)…(
-2)…(![]() -100)在
-100)在![]() =0处的导数值为( )
=0处的导数值为( )
A、0 B、
(9)曲线![]() 在点
在点![]() 处的切线与坐标轴围成的三角形面积为( )
处的切线与坐标轴围成的三角形面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
(二).填空题
(1).垂直于直线2x+6y+1=0且与曲线y = x3+3x-5相切的直线方程是 。
(2).设f ( x ) = x3-![]() x2-2x+5,当
x2-2x+5,当![]() 时,f ( x ) < m恒成立,则实数m的取值范围为
.
时,f ( x ) < m恒成立,则实数m的取值范围为
.
(3).函数y = f ( x ) = x3+ax2+bx+a2,在x = 1时,有极值10,则a = ,b = 。
(4).已知函数![]() 在
在![]() 处有极值,那么
处有极值,那么![]() ;
;![]()
![]()
(5).已知函数![]() 在R上有两个极值点,则实数
在R上有两个极值点,则实数![]() 的取值范围是
的取值范围是
![]()
(6).已知函数![]() 既有极大值又有极小值,则实数
既有极大值又有极小值,则实数![]() 的取值范围是
的取值范围是 ![]()
(7).若函数![]() 是R是的单调函数,则实数
是R是的单调函数,则实数![]() 的取值范围是
的取值范围是 ![]()
(8).设点![]() 是曲线
是曲线![]() 上的任意一点,
上的任意一点,![]() 点处切线倾斜角为
点处切线倾斜角为![]() ,则角
,则角![]() 的取值范围是 。
的取值范围是 。
(三).解答题
1.已知函数![]() 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M![]() 处的切线方程为
处的切线方程为![]() .
.
(Ⅰ)求函数![]() 的解析式;(Ⅱ)求函数
的解析式;(Ⅱ)求函数![]() 的单调区间.
的单调区间.
2.已知函数![]() 在
在![]() 处取得极值.
处取得极值.
(Ⅰ)讨论![]() 和
和![]() 是函数
是函数![]() 的极大值还是极小值;
的极大值还是极小值;
(Ⅱ)过点![]() 作曲线
作曲线![]() 的切线,求此切线方程.
的切线,求此切线方程.
3.已知向量![]() 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
4.已知函数![]()
(1)当![]() 时,求函数
时,求函数![]() 极小值;(2)试讨论曲线
极小值;(2)试讨论曲线![]() 与
与![]() 轴公共点的个数。
轴公共点的个数。
5.已知![]() 是函数
是函数![]() 的一个极值点,其中
的一个极值点,其中![]() ,
,
(I)求![]() 与
与![]() 的关系式;
(II)求
的关系式;
(II)求![]() 的单调区间;
的单调区间;
(III)当![]() 时,函数
时,函数![]() 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3![]() ,求
,求![]() 的取值范围.
的取值范围.
6.已知两个函数![]() ,
,![]() .
.
(Ⅰ)若对任意![]() [-3,3],都有
[-3,3],都有![]() ≤
≤![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若对任意![]() [-3,3],
[-3,3],![]() [-3,3],都有
[-3,3],都有![]() ≤
≤![]() 成立,求实数
成立,求实数![]() 的取值范围
的取值范围
7.设函数![]() 在
在![]() 及
及![]() 时取得极值.
时取得极值.
(Ⅰ)求a、b的值;
(Ⅱ)若对于任意的![]() ,都有
,都有![]() 成立,求c的取值范围.
成立,求c的取值范围.
8.设函数![]() .
.
(Ⅰ)求![]() 的最小值
的最小值![]() ;
;
(Ⅱ)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围
的取值范围
9.已知![]() 在区间[0,1]上是增函数,在区间
在区间[0,1]上是增函数,在区间![]() 上是减函数,又
上是减函数,又![]()
(Ⅰ)求![]() 的解析式;(Ⅱ)若在区间
的解析式;(Ⅱ)若在区间![]() (m>0)上恒有
(m>0)上恒有![]() ≤x成立,求m的取值范围.
≤x成立,求m的取值范围.
10.用长为
11.某市旅游部门开发一种旅游纪念品,每件产品的成本是15元,销售价是20元,月平均销售a件.通过改进工艺,产品的成本不变,质量和技术含金量提高,市场分析的结果表明,如果产品的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为x2.记改进工艺后,旅游部门销售该纪念品的月平均利润是y(元).
,那么月平均销售量减少的百分率为x2.记改进工艺后,旅游部门销售该纪念品的月平均利润是y(元).
(1)写出y与x的函数关系式;
(2)改进工艺后,试确定该纪念品的销售价,使得旅游部门销售该纪念品的月平均利润最大.
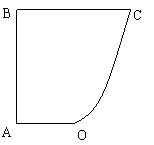
12.某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形的高科技工业园区.已知AB⊥BC,OA//BC,且AB=BC=2 AO=
 |
13.设三次函数![]() 在
在![]() 处取得极值,其图象在
处取得极值,其图象在![]() 处的切线的斜率为
处的切线的斜率为![]() .
.
(1)求证:![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(3)问是否存在实数![]() (
(![]() 是与
是与![]() 无关的常数),当
无关的常数),当![]() 时,恒有
时,恒有![]() 恒成立?若存在,试求出
恒成立?若存在,试求出![]() 的最小值;若不存在,请说明理由.
的最小值;若不存在,请说明理由.
14.已知函数![]() 在区间[0,1]单调递增,在区间
在区间[0,1]单调递增,在区间![]() 单调递减.
单调递减.
(1)求a的值;
(2)若点![]() 在函数f(x)的图象上,求证点A关于直线
在函数f(x)的图象上,求证点A关于直线![]() 的对称点B也在函数f(x)的图象上;
的对称点B也在函数f(x)的图象上;
(3)是否存在实数b,使得函数![]() 的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的值;若不存在,试说明理
的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的值;若不存在,试说明理
15.已知![]() 上是减函数,且
上是减函数,且![]() 。
。
(1)求![]() 的值,并求出
的值,并求出![]() 和
和![]() 的取值范围。 (2)求证
的取值范围。 (2)求证![]() 。
。
(3)求![]() 的取值范围,并写出当
的取值范围,并写出当![]() 取最小值时的
取最小值时的![]() 的解析式。
的解析式。
16.设函数![]()
![]() 为奇函数,其图象在点
为奇函数,其图象在点![]() 处的切线与直线
处的切线与直线![]() 垂直,导函数
垂直,导函数![]() 的最小值为
的最小值为![]() .
.
(Ⅰ)求![]() ,
,![]() ,
,![]() 的值;
的值;
(Ⅱ)求函数![]() 的单调递增区间,并求函数
的单调递增区间,并求函数![]() 在
在![]() 上的最大值和最小值.
上的最大值和最小值.
参考解答
一.BBDDD CDDA二.1、y=3x-5 2、m>7 3、4 -11
4、![]() 5、
5、![]() 6、
6、![]() 7、
7、![]() 8、
8、![]() 三.1.解:(Ⅰ)由
三.1.解:(Ⅰ)由![]() 的图象经过P(0,2),知d=2,所以
的图象经过P(0,2),知d=2,所以![]()
![]() 由在
由在![]() 处的切线方程是
处的切线方程是![]() ,知
,知![]()
![]() 故所求的解析式是
故所求的解析式是 ![]() (2)
(2)![]() 解得
解得 ![]() 当
当![]() 当
当![]() 故
故![]() 内是增函数,在
内是增函数,在![]() 内是减函数,在
内是减函数,在![]() 内是增函数.
内是增函数.
2.(Ⅰ)解:![]() ,依题意,
,依题意,![]() ,即
,即
![]() 解得
解得![]() .
.
∴![]() .
.
令![]() ,得
,得![]() .
.
若![]() ,则
,则![]() ,
,
故![]() 在
在![]() 上是增函数,
上是增函数,![]() 在
在![]() 上是增函数.
上是增函数.
若![]() ,则
,则![]() ,故
,故![]() 在
在![]() 上是减函数.
上是减函数.
所以,![]() 是极大值;
是极大值;![]() 是极小值.
是极小值.
(Ⅱ)解:曲线方程为![]() ,点
,点![]() 不在曲线上.
不在曲线上.
设切点为![]() ,则点M的坐标满足
,则点M的坐标满足![]() .
.
因![]() ,故切线的方程为
,故切线的方程为![]()
注意到点A(0,16)在切线上,有![]()
化简得![]() ,解得
,解得![]() .
.
所以,切点为![]() ,切线方程为
,切线方程为![]() .
.
3.解:依定义![]()
![]()
![]() 的图象是开口向下的抛物线,
的图象是开口向下的抛物线,
![]()
![]()
4.解:(1)![]()
![]() 极小值为
极小值为![]()
(2)①若![]() ,则
,则![]() ,
,![]() 的图像与
的图像与![]() 轴只有一个交点;
轴只有一个交点;
②若![]() ,
, ![]()
![]() 极大值为
极大值为![]() ,
,![]() 的极小值为
的极小值为![]() ,
,
![]() 的图像与
的图像与![]() 轴有三个交点;
轴有三个交点;
③若![]() ,
,![]() 的图像与
的图像与![]() 轴只有一个交点;
轴只有一个交点;
④若![]() ,则
,则![]() ,
,![]() 的图像与
的图像与![]() 轴只有一个交点;
轴只有一个交点;
⑤若![]() ,由(1)知
,由(1)知![]() 的极大值为
的极大值为![]() ,
,![]() 的图像与
的图像与![]() 轴只有一个交点;
轴只有一个交点;
综上知,若![]() 的图像与
的图像与![]() 轴只有一个交点;若
轴只有一个交点;若![]() ,
,![]() 的图像与
的图像与![]() 轴有三个交点。
轴有三个交点。
5.解(I)![]() 因为
因为![]() 是函数
是函数![]() 的一个极值点,
的一个极值点,
所以![]() ,即
,即![]() ,所以
,所以![]()
(II)由(I)知,![]() =
=![]()
当![]() 时,有
时,有![]() ,当
,当![]() 变化时,
变化时,![]() 与
与![]() 的变化如下表:
的变化如下表:
|
|
|
|
| 1 |
|
|
|
| 0 |
| 0 |
|
|
| 调调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
故有上表知,当![]() 时,
时,![]() 在
在![]() 单调递减,
单调递减,
在![]() 单调递增,在
单调递增,在![]() 上单调递减.
上单调递减.
(III)由已知得![]() ,即
,即![]()
又![]() 所以
所以![]() 即
即![]() ①
①
设![]() ,其函数开口向上,由题意知①式恒成立,
,其函数开口向上,由题意知①式恒成立,
所以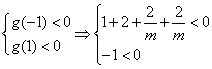 解之得
解之得
![]() 又
又![]()
所以![]()
即![]() 的取值范围为
的取值范围为![]()
6.略
7.解:(Ⅰ)![]() ,
,
因为函数![]() 在
在![]() 及
及![]() 取得极值,则有
取得极值,则有![]() ,
,![]() .
.
即![]()
解得![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)可知,![]() ,
,
![]() .
.
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
所以,当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,又
,又![]() ,
,![]() .
.
则当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
因为对于任意的![]() ,有
,有![]() 恒成立,
恒成立,
所以 ![]() ,
,
解得 ![]() 或
或![]() ,
,
因此![]() 的取值范围为
的取值范围为![]() .
.
8.解:(Ⅰ)![]() ,
,
![]() 当
当![]() 时,
时,![]() 取最小值
取最小值![]() ,
,
即![]() .
.
(Ⅱ)令![]() ,
,
由![]() 得
得![]() ,
,![]() (不合题意,舍去).
(不合题意,舍去).
当![]() 变化时
变化时![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
| 递增 | 极大值 | 递减 |
![]() 在
在![]() 内有最大值
内有最大值![]() .
.
![]() 在
在![]() 内恒成立等价于
内恒成立等价于![]() 在
在![]() 内恒成立,
内恒成立,
即等价于![]() ,
,
所以![]() 的取值范围为
的取值范围为![]()
9.解:(Ⅰ)![]() ,由已知
,由已知![]() ,
,
即![]() 解得
解得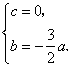
![]() ,
,![]() ,
,![]() ,
,![]() .
.
(Ⅱ)令![]() ,即
,即![]() ,
,
![]() ,
,![]() 或
或![]() .
.
又![]() 在区间
在区间![]() 上恒成立,
上恒成立,![]()
10.解:设长方体的宽为x(m),则长为2x(m),高为
![]() .
.
故长方体的体积为
![]()
从而![]()
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x<![]() 时,V′(x)<0,
时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。
从而最大体积V=V′(x)=9×12-6×13(m3),此时长方体的长为
11.解:(1)改进工艺后,每件产品的销售价为20(1+x)元
月平均销售量为![]() 件则月平均利润
件则月平均利润![]() (元)
(元)
y与x的函数关系式为![]()
(1)
令![]()
当![]()
即函数![]() 在
在![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 取得最大值.
取得最大值.
所以改进工艺后,产品的销售价提高的百分率为![]() 元时,旅游部门销售该纪念品的月平均利润最大.
元时,旅游部门销售该纪念品的月平均利润最大.
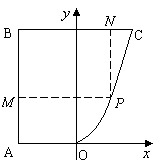
12.解:以O为原点,OA所在直线为![]() 轴建立直角坐标系(如图)
轴建立直角坐标系(如图)
依题意可设抛物线的方程为![]()
故曲线段OC的方程为![]() 3分
3分
设P(![]() )
)![]() 是曲线段OC上的任意一点,则PQ=2+
是曲线段OC上的任意一点,则PQ=2+![]() ,PN=4-
,PN=4-![]() 2. 5分
2. 5分
∴工业园区面积S=PQ·PN=(2+![]() )(4-
)(4-![]() 2)=8-
2)=8-![]() 3-2
3-2![]() 2+4
2+4![]() . 6分
. 6分
 ∴S′=-3
∴S′=-3![]() 2-4
2-4![]() +4,令S′=0
+4,令S′=0![]()
又![]() 7分
7分
当![]() 时,S′>0,S是
时,S′>0,S是![]() 的增函数;8分
的增函数;8分
当![]() )时,S′<0,S是
)时,S′<0,S是![]() 的减函数. 9分
的减函数. 9分
![]() 时,S取到极大值,此时PM=2+
时,S取到极大值,此时PM=2+![]() =
=![]()
![]() 10分
10分
当![]()
![]() 11分
11分
答:把工业园区规划成长为![]() 宽为
宽为![]() 时,工业园区的面积最大,最大面积为
时,工业园区的面积最大,最大面积为
13.解:(1)![]() 由题设,得
由题设,得![]() ①
①
![]() ②
②
∵![]()
由①代入②得![]() ,
,
得![]() ∴
∴![]() 或
或![]() ③
③
将![]() 代入
代入![]() 中,得
中,得![]() ④
④
由③、④得![]() ;
;
(2)由(1)知,![]() 的判别式:
的判别式:![]()
∴方程![]() 有两个不等的实根
有两个不等的实根![]() ,又
,又![]()
∴![]() ,∴当
,∴当![]() 或
或![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,∴函数
,∴函数![]() 的单调增区间是
的单调增区间是![]()
∴![]() ,由
,由![]() 知
知![]()
∵函数![]() 在区间
在区间![]() 上单调递增,∴
上单调递增,∴![]()
∴![]() ,即
,即![]() 的取值范围是
的取值范围是![]() ;
;
(3)由![]() ,即
,即![]() ,
,
∵![]() ,
,![]()
![]() ∴
∴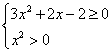
∴![]() 或
或![]() .由题意,得
.由题意,得![]()
∴![]() ,∴存在实数
,∴存在实数![]() 满足条件,即
满足条件,即![]() 的最小值为
的最小值为![]() .
.
14.解:(1)由函数![]() 在区间[0,1)单调递增,在区间[1,2)单调递减,
在区间[0,1)单调递增,在区间[1,2)单调递减,
![]() ,
,![]() .
.
![]()
(2)点![]() ,
,
| |
∴点A关于直线x=1的对称点B也在函数f(x)的图象上.
(3)函数![]() 的图象与函数f(x)的图象恰有3个交点,等价于方程
的图象与函数f(x)的图象恰有3个交点,等价于方程
![]() 个不等实根.
个不等实根.
![]() .
.
![]() 是其中一个根,
是其中一个根,![]() 有两个非零不等实根.
有两个非零不等实根.
![]()
15.(1)![]()
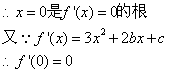
![]()

![]()
(2)![]()
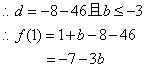
![]()
(3)![]()
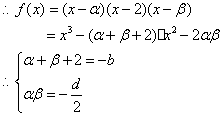

![]() ·
·
16
(Ⅰ)∵![]() 为奇函数,
为奇函数,
∴![]()
即![]()
∴![]()
∵![]() 的最小值为
的最小值为![]()
∴![]()
又直线![]() 的斜率为
的斜率为![]()
因此,![]()
∴![]() ,
,![]() ,
,![]() .
.
(Ⅱ)![]() .
.
![]() ,列表如下:
,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 极大 |
| 极小 |
|
所以函数![]() 的单调增区间是
的单调增区间是![]() 和
和![]()
∵![]() ,
,![]() ,
,![]()
∴![]() 在
在![]() 上的最大值是
上的最大值是![]() ,最小值是
,最小值是![]()