高二数学下学期学业水平测试模拟试题(人教A版)
本试卷分第I卷(选择题)和第II卷(非选择题)两部分,第I卷第I至第2页,第II卷第3至第4页![]() 全卷满分100分,考试时间90分钟
全卷满分100分,考试时间90分钟![]()
第Ⅰ卷
一、选择题。本卷共18小题,每小题3分,共54分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把符合要求的选项填写在后面的答题卡中.
1.设集合![]() ,则
,则![]() ( B
)
( B
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2![]()
![]() ( C
)A.
( C
)A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3![]() 下列几何体各自的三视图中,有且仅有两个视图相同的是( D )
下列几何体各自的三视图中,有且仅有两个视图相同的是( D )

A![]() ①② B
①② B![]() ①③ C
①③ C![]() ①④ D
①④ D![]() ②④
②④
4.函数![]() 的定义域为( A )
的定义域为( A )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
5![]() 下列说法错误的是 ( B )
下列说法错误的是 ( B )
A![]() 在统计里,把所需考察对象的全体叫作总体
在统计里,把所需考察对象的全体叫作总体
B![]() 一组数据的平均数一定大于这组数据中的每个数据
一组数据的平均数一定大于这组数据中的每个数据
C![]() 平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
平均数、众数与中位数从不同的角度描述了一组数据的集中趋势
D![]() 一组数据的方差越大,说明这组数据的波动越大
一组数据的方差越大,说明这组数据的波动越大
6![]() 已知向量
已知向量![]() ,若
,若![]() 与
与![]() 垂直,则
垂直,则![]() ( C
)
( C
)
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]() 4
4
7![]() 用二分法求方程
用二分法求方程![]() 的近似根的算法中要用哪种算法结构( D )
的近似根的算法中要用哪种算法结构( D )
A![]() 顺序结构 B
顺序结构 B![]() 条件结构 C
条件结构 C![]() 循环结构 D
循环结构 D![]() 以上都用
以上都用
8![]() 从装有
从装有![]() 个红球和
个红球和![]() 个黒球的口袋内任取
个黒球的口袋内任取![]() 个球,那么互斥而不对立的两个事件是(
D )
个球,那么互斥而不对立的两个事件是(
D )
A![]() 至少有一个黑球与都是黑球
B
至少有一个黑球与都是黑球
B![]() 至少有一个红球与都是黑球
至少有一个红球与都是黑球
C![]() 至少有一个黑球与至少有
至少有一个黑球与至少有![]() 个红球 D
个红球 D![]() 恰有
恰有![]() 个黑球与恰有
个黑球与恰有![]() 个黑球
个黑球
9.不等式![]() 的解集是( C
)
的解集是( C
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10![]() 若向量
若向量![]() 、
、![]() 满足
满足![]() =
=![]() =1,
=1,![]() 与
与![]() 的夹角为
的夹角为![]() ,则
,则![]() ( B )
( B )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]() 2
2
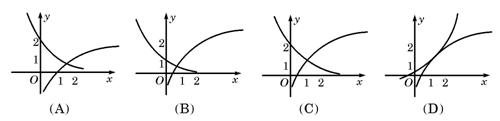 |
11.函数f(x)=1+log2x与g(x)=2-x+1在同一直角坐标系下的图象大致是( C )
12.若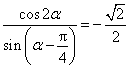 ,则
,则![]() 的值为( C )
的值为( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13 先后抛掷骰子三次,则至少一次正面朝上的概率是( D )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
14.设等差数列![]() 的公差
的公差![]() 不为0,
不为0,![]()
![]() 若
若![]() 是
是![]() 与
与![]() 的等比中项,则
的等比中项,则![]() ( B )
( B )
A ![]() 2 B
2 B ![]() 4 C
4 C ![]() 6 D
6 D ![]() 8
8
15![]() 在△ABC中,若
在△ABC中,若![]() ,则其面积等于( D )
,则其面积等于( D )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
16![]() 已知简谐运动
已知简谐运动![]() 的图象经过点(0,1),则该简谐运动的最小正周期
的图象经过点(0,1),则该简谐运动的最小正周期![]() 和初相
和初相![]() 分别为( A )
分别为( A )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
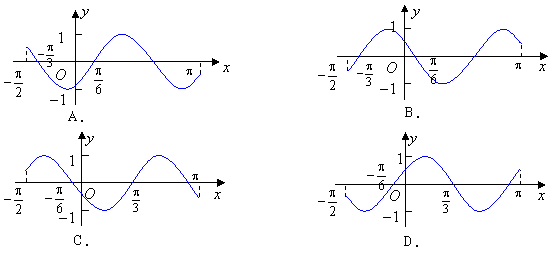
17.函数![]() 在区间
在区间![]() 的简图是( A )
的简图是( A )
18![]() 若函数
若函数![]() 在
在![]() 上是单调函数,则
上是单调函数,则![]() 的取值范围是( C )
的取值范围是( C )
A![]()
![]() B
B![]()
![]() C
C![]()
![]() D
D![]()
![]()
第II卷
二、填空题:本大题共4小题,每小题4分,共16分![]()
19![]() 函数
函数![]() 的图象为
的图象为![]() ,如下结论中正确的是 (填写正确结论的序号) ①②③
,如下结论中正确的是 (填写正确结论的序号) ①②③
①图象![]() 关于直线
关于直线![]() 对称;②图象
对称;②图象![]() 关于点
关于点![]() 对称;③函数
对称;③函数![]() 在区间
在区间![]() 内是增函数;④由
内是增函数;④由![]() 的图角向右平移
的图角向右平移![]() 个单位长度可以得到图象
个单位长度可以得到图象![]()
![]()
20![]() 若数列
若数列![]() 的前
的前![]() 项和
项和![]() ,则此数列的通项公式为 .2n-11
,则此数列的通项公式为 .2n-11
21 ![]() 某校有学生2000人,其中高三学生500人,为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本,则样本中高三学生的人数为 50
某校有学生2000人,其中高三学生500人,为了解学生的身体素质情况,采用按年级分层抽样的方法,从该校学生中抽取一个200人的样本,则样本中高三学生的人数为 50 ![]()
22 ![]()
![]() 中的
中的![]() 满足约束条件
满足约束条件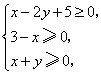 则
则![]() 的最小值是
的最小值是
![]()
![]()
三、解答题:本大题共3小题,共30分![]() 解答应写出文字说明,证明过程或演算步骤
解答应写出文字说明,证明过程或演算步骤![]()
23 ![]() 在如图所示的几何体中,
在如图所示的几何体中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,
,![]() 是
是![]() 的中点
的中点
![]()
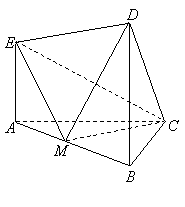 (I)求证:
(I)求证:![]() ;
;
(II)求![]() 与平面
与平面![]() 所成的角的正切值
所成的角的正切值
![]()
方法一:
(I)证明:因为![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]()
![]()
又因为![]() 平面
平面![]() ,
,
所以![]()
![]()
(II)解:连结![]() ,设
,设![]() ,则
,则![]() ,
,
在直角梯形![]() 中,
中,
![]() ,
,![]() 是
是![]() 的中点,
的中点,
所以![]() ,
,![]() ,
,![]() ,
,
因此![]()
![]()
因为![]() 平面
平面![]() ,
,
所以![]() ,
,
因此![]() 平面
平面![]() ,
,
故![]() 是直线
是直线![]() 和平面
和平面![]() 所成的角
所成的角
![]()
在![]() 中,
中,
![]() ,
,![]() ,
,
![]()
![]()
方法二:
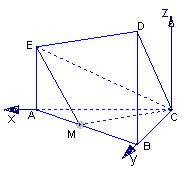 如图,以点
如图,以点![]() 为坐标原点,以
为坐标原点,以![]() ,
,![]() 分别为
分别为![]() 轴和
轴和![]() 轴,过点
轴,过点![]() 作与平面
作与平面![]() 垂直的直线为
垂直的直线为![]() 轴,建立直角坐标系
轴,建立直角坐标系![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
(I)证明:因为![]() ,
,![]() ,
,
所以![]() ,
,
故![]()
![]()
(II)解:设向量![]() 与平面
与平面![]() 垂直,则
垂直,则![]() ,
,![]() ,
,
即![]() ,
,![]()
![]()
因为![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
即![]() ,
,
因为![]() ,
,
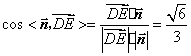 ,
,
![]() 与平面
与平面![]() 所成的角
所成的角![]() 是
是![]() 与
与![]() 夹角的余角,
夹角的余角,
所以![]()
![]()
24![]() 求过点
求过点![]() 且圆心在直线
且圆心在直线![]() 上的圆的方程
上的圆的方程![]()
解:设圆心为![]() ,而圆心在线段
,而圆心在线段![]() 的垂直平分线
的垂直平分线![]() 上,
上,
即![]() 得圆心为
得圆心为![]() ,
,![]()
![]()
25.一个水池有若干出水量相同的水龙头,如果所有的水龙头同时放水,那么24min可以注满水池。如果开始时全部开放,以后每隔相等的时间关闭一个水龙头,到最后一个水龙头关闭时,恰好注满水池,而且最后一个水龙头放水时间恰好时第一个水龙头放水时间的5倍,问最后关闭水龙头放水时间是多少?
解:设共有n个水龙头,每个水龙头开放时间依次是![]()
已知![]() 数列
数列![]() 是等差数列,每个水龙头1min放水
是等差数列,每个水龙头1min放水![]()
![]() ,即
,即![]() ,即
,即![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,![]()
![]() ,
,![]() ,
,![]()
故最后关闭的水龙头放水40min.