高二数学下学期期末复习题(一) 08年6月
班级 学号 得分
一.填空题
1. 在复平面内,与复数![]() 的共轭复数对应的点位于第_________象限.
的共轭复数对应的点位于第_________象限.
2. 若回归直线方程中的回归系数b=0时,则相关系数r=___________.
3. 若数集![]() 则
则![]() 的值为____________.
的值为____________.
4. 已知x与y之间的一组数据:
| x | 0 | 1 | 2 | 3 |
| y | 1 | 3 | 5 | 7 |
则y与x的线性回归方程为![]() =bx+a必过点____________.
=bx+a必过点____________.
5. “![]() ”是“
”是“![]() ”的_______________条件.
”的_______________条件.
6. ![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,则
,则![]() ___________.
___________.
7. 定义:复数![]() 是
是![]() 的转置复数,记为
的转置复数,记为![]() ;复数
;复数![]() 是
是
![]() 的共轭复数,记为
的共轭复数,记为![]() .给出下列命题:①
.给出下列命题:①![]() ②
②![]()
③![]() .其中所有真命题的序号为_____________.
.其中所有真命题的序号为_____________.
8. 已知集合![]() 若
若![]() ,则实数
,则实数![]() 的取值范围是_____.
的取值范围是_____.
9. 设函数![]() 在
在![]() 处取极值,则
处取极值,则![]() 的值为___________.
的值为___________.
10.将函数![]() 的图像,仅向右平移
的图像,仅向右平移![]() ,或仅向左平移
,或仅向左平移![]() ,所得到的函数图像均关于原点对称,则
,所得到的函数图像均关于原点对称,则![]() ____________.
____________.
11. 若函数![]() 在
在![]() 上是增函数,则
上是增函数,则![]() 的取值集合为____________.
的取值集合为____________.
12.函数![]() 在区间
在区间![]() 上的最大值
上的最大值![]() 的最小值是___________.
的最小值是___________.
13.已知函数![]() 且
且![]() 无零点.现给出下列命题:①
无零点.现给出下列命题:①![]() 一定无极值点;②
一定无极值点;②![]() 恒成立;③
恒成立;③![]() 恒成立.其中所有不正确命题的序号是____________.
恒成立.其中所有不正确命题的序号是____________.
14. 下面有五个命题:
①函数![]() 的最小正周期是
的最小正周期是![]() . ②终边在
. ②终边在![]() 轴上的角的集合是
轴上的角的集合是![]()
③在同一坐标系中,函数![]() 的图像和函数
的图像和函数![]() 的图像有三个公共点.
的图像有三个公共点.
④把函数![]() 的图像向右平移
的图像向右平移![]() 得到
得到![]() 的图像.
的图像.
⑤函数![]() 在
在![]() 上是减函数.其中真命题的序号是___________.
上是减函数.其中真命题的序号是___________.
二.解答题
15.打鼾不仅影响别人休息,而且可能与患某种疾病有关,下表是一次调查所得的数据,试问:每一晚都打鼾与患心脏病有关吗?
| 患心脏病 | 未患心脏病 | 合计 | |
| 每一晚都打鼾 | 30 | 224 | 254 |
| 不打鼾 | 24 | 1355 | 1379 |
| 合计 | 54 | 1579 | 1633 |
16. 已知集合![]()
(1)当![]() 时,求
时,求![]() ; (2)求使
; (2)求使![]() 的实数
的实数![]() 的取值范围.
的取值范围.
17. 求同时满足下列两个条件的所有复数![]() (1)
(1)![]() ,且
,且![]() (2)
(2)![]() 的实部和虚部都是整数.
的实部和虚部都是整数.
18.![]() 是一矩形OEFG边界上的两动点,点A在EF上,点B在GF上,
是一矩形OEFG边界上的两动点,点A在EF上,点B在GF上,
∠![]() °,
°,![]()
![]() 设∠
设∠![]() .
.
(1)
写出△AOB的面积关于![]() 的函数表达式
的函数表达式![]() ;
;
(2)
求函数![]() 的值域.
的值域.
(提供公式:![]() )
)
19.设函数![]() 且
且![]() 构成等差数列.
构成等差数列.
(1)
求![]() 的解析式;
的解析式;
(2)
在函数![]() 的图像上是否存在点P,使过点P的切线与该图像再无其它公共点?若存在,求出所有满足条件的点的坐标;若不存在,说明理由;
的图像上是否存在点P,使过点P的切线与该图像再无其它公共点?若存在,求出所有满足条件的点的坐标;若不存在,说明理由;
(3)
设![]() 为函数
为函数![]() 图像上的任一点,试问点
图像上的任一点,试问点![]() 是否也在该图像上?为什么?
是否也在该图像上?为什么?
20.已知函数![]() 且实数
且实数![]() 满足:
满足:![]() 或
或
![]() .
.
(1)
试求![]() 的取值范围;
的取值范围;
(2)
试判断:①![]() ②
②![]() ③
③![]() ,是否为定值?若是定值,求出其值;若不是定值,把不是定值的表示为函数
,是否为定值?若是定值,求出其值;若不是定值,把不是定值的表示为函数![]() ,并写出
,并写出![]() 的表达式;
的表达式;
(3)
对于(2)中的函数![]() ,若不等式
,若不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
高二期末复习题(一)(参考答案)
二.填空题
1. 二;2. 0;3. 0或4;4.(1.5,4);5. 充分不必要;6. 1;7. ①②;8.(2,3);
9. 2;10. ![]() ;11.
;11.![]() 12.
12. ![]() ; 13. ①③④;
14.①④
; 13. ①③④;
14.①④
二.解答题
15. 解:假设![]() :打鼾与患心脏病无关,
:打鼾与患心脏病无关,
∴![]()
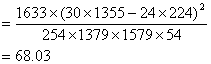
因为![]() ,所以有99.9%以上的把握认为打鼾与患心脏病有关.
,所以有99.9%以上的把握认为打鼾与患心脏病有关.
答:99.9%以上的把握认为打鼾与患心脏病有关.
16. 解:(1)当![]() =2时,A=(2,7),B=(4,5)∴ A
=2时,A=(2,7),B=(4,5)∴ A![]() B=(4,5).
B=(4,5).
(2)∵ B=(
当a<![]() 时,A=(
时,A=(![]() A,必须
A,必须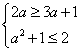 ,此时a=-1;
,此时a=-1;
当a=![]() 时,A=
时,A=![]() ,使B
,使B![]() A的a不存在;
A的a不存在;
当a>![]() 时,A=(2,
时,A=(2,![]() A,必须
A,必须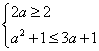 ,此时1≤a≤3.
,此时1≤a≤3.
综上可知,使B![]() A的实数a的取值范围为[1,3]∪{-1}
.
A的实数a的取值范围为[1,3]∪{-1}
.
17.解:设![]() ,∴
,∴![]()
![]()
![]()
当![]() 时,
时,![]() 舍去.
舍去.
当![]() 时,
时,![]()
![]() .
.
∴![]() 或
或![]()
![]()
![]() .
.
18.解:(1)∵OE=1,![]() ∴∠
∴∠![]()
![]()
当![]() 时,△AOB的两顶点
时,△AOB的两顶点![]() 均在
均在![]() 上,且
上,且![]() +
+![]() ,
,
∴![]() △AOB=
△AOB=![]() △EOB-
△EOB-![]() △EOA=
△EOA=![]() +
+![]()
![]()
=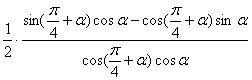 =
=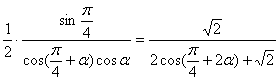 .
.
当![]() 时,
时,![]() 点在
点在![]() 上,B点在
上,B点在![]() 上,且
上,且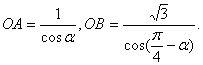
∴![]() △AOB=
△AOB=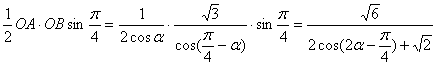 .
.
综上,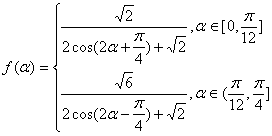
(2)由(1)得,当![]() 时,
时,![]()
![]()
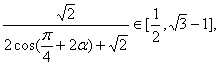
且当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
当![]() 时,
时, ![]()
![]()
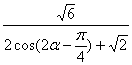
![]()
且当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ∴值域为
∴值域为![]()
19.解:(1)![]()
(2)设点P存在,坐标为![]() ,∴切线斜率
,∴切线斜率![]()
∴切线方程:![]() .又∵
.又∵![]()
∴![]() ,∴点P存在,坐标为
,∴点P存在,坐标为![]() .
.
(3)设![]() ,∵
,∵![]()
=![]() ,∴点
,∴点![]() 也在该图像上.
也在该图像上.
20.解:(1)![]()
(2)①![]() 为定值;
为定值;
②![]() 为定值;
为定值;
③![]()
∴![]()
![]() ,其中
,其中![]()
(3)令![]() 则
则![]() 令
令![]() 则
则![]() ,
,
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() 当
当![]() 时,
时,![]()
∴![]() 有极大值
有极大值![]() 有极小值
有极小值![]() ,又∵
,又∵![]()
∴![]() ∴
∴![]() .
.